调频引信粗糙面目标与干扰信号识别

郝新红，杜涵宇，陈齐乐

（北京理工大学 机电动态控制重点实验室，北京100081）

调频（FM）无线电引信具有定距精度高、算法相对简单、硬件容易实现等优点，目前已经在常规弹药中得到了大规模应用［1-3］。在调频引信信号处理算法设计过程中，通常认为引信目标是点目标，但实际对地引信的目标大地表面是一种粗糙的面目标。随着无线电引信干扰技术的不断发展，以数字射频存储（DRFM）干扰为代表的转发式干扰已经可以完全模拟点目标回波［4-5］，这给调频引信造成了致命威胁。

在无线电引信和雷达领域已经有大量对于面目标特性的研究，对面目标特性的研究主要有2种方法。一种是使用多点散射叠加模拟面目标或体目标回波信号［6-9］，如文献［6］使用3个点模拟面目标，指出多点目标回波造成引信多普勒信号频谱展宽，而且弹目越接近，频谱展宽越大；文献［7］建立了引信远场单点目标和近场多点目标模型，将信号的调幅带宽和调频带宽作为特征参量，对干扰信号和体目标信号进行分类识别。但是多点散射叠加建模方法比较简单，DRFM 干扰系统可以模拟［10-11］。另一种方法是通过近似法研究粗糙面散射特性［12-15］，在雷达领域较为常见，如文献［12］用随机粗糙面模拟实际地面，利用基尔霍夫近似（KA）法和微扰近似法（SPM）计算了粗糙面的雷达后向和双站散射系数；文献［13］分析了连续波调频雷达高度表随机粗糙面回波和差频信号的统计特性，对差频信号的二维功率谱密度进行了计算和仿真。基于近似法的粗糙面目标建模方法更贴近实际情况，可以用于引信面目标建模。

针对对地调频引信粗糙面目标与干扰信号识别的问题，本文对调频引信随机粗糙面回波信号和差频信号进行了建模，利用二维距离-速度提取方法提取其差频频率和多普勒频率，对点目标和随机粗糙面目标作用下调频引信差频信号的二维频率特性进行了仿真。

1 调频引信粗糙面差频信号建模

根据瑞利准则，对于工作在S波段的调频引信，稍有起伏的土地或覆盖植被的地面即可被认为是粗糙面。当粗糙面的表面相关长度和高度起伏均方差大于波长时，可以使用基尔霍夫近似法进行粗糙面回波信号建模。本文使用一维随机粗糙面代替粗糙地面进行建模，即在xOy平面内，只有x维度存在粗糙度，并假设其粗糙度参数和引信工作波长符合基尔霍夫近似法要求。

设一维随机粗糙面高度起伏为z=f（x），其参考平面为z=0，引信在t=0时刻高度为H，横坐标为x=0，运动速度为v，运动方向与垂直方向夹角为α，在引信天线主瓣辐射范围内一维粗糙面上点P（x，f（x）），引信到P点距离为ρ，引信与P点连线和垂直方向夹角为θ，引信与粗糙面的位置关系如图1所示。

若引信发射频率为f0的点频信号，则根据基尔霍夫近似法计算，粗糙面散射后引信接收到回波信号为［13］

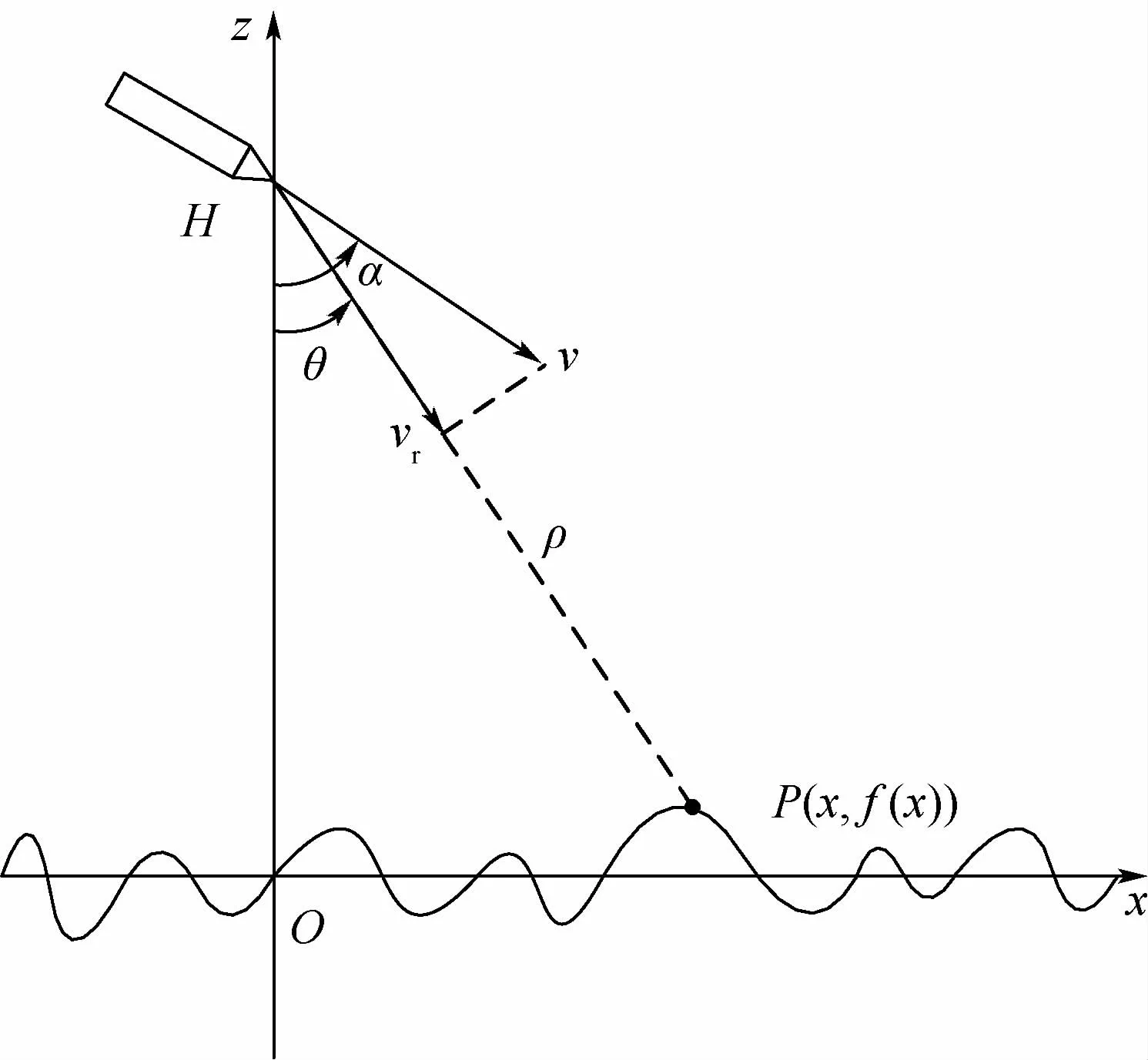
图1 引信与粗糙面的位置关系Fig.1 Positional relationship between fuze and rough surface

式中：i为谐波次数（i=1，2，…，+∞）；ai为发射信号的傅里叶系数；fm为信号调频。

根据式（1）、式（2）可得出调频引信粗糙面回波信号为

式中：ki为第i次谐波的波数，ki=2πifm/c。

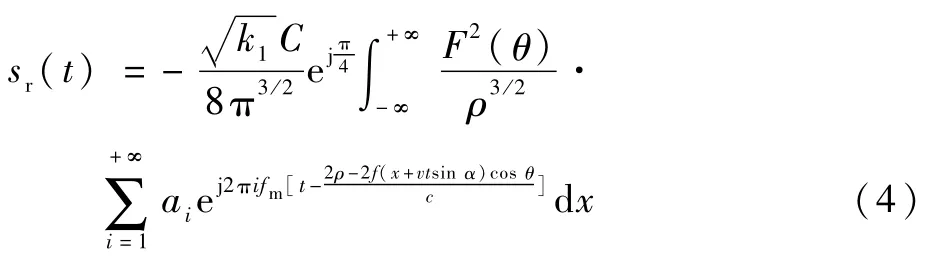
把调频引信粗糙面回波信号与本地参考信号进行混频，得到其差频信号。根据式（2）、式（4）可以得到粗糙面作用下调频引信差频信号表达式为

式中：“*”表示共轭。

式中：n=0，1，…，+∞。

2 调频引信二维距离-速度提取方法

传统的调频引信大多采用调频谐波定距方法，其信号处理方法是对差频信号进行二次混频和多普勒检波，提取出特定次谐波的多普勒检波信号［2］。调频谐波定距方法本质是从频域提取与距离信息一一对应的差频频率，因此难以对抗能够模拟点目标回波的DRFM 干扰。因此，本文提出一种基于粗糙面目标的调频引信距离-速度二维特征提取方法，直接对基于粗糙面目标特性的差频信号进行距离-多普勒处理，通过第1维傅里叶变换提取一个调制周期内与距离相对应的差频频率，再通过第2维傅里叶变换提取与速度相对应的多普勒频率，进而提取出其距离和速度信息。调频引信二维距离-速度提取方法示意图如图2所示，其中，fB为差频频率，fD为多普勒频率。

图2 调频引信二维距离-速度提取方法Fig.2 Two-dimensional distance-speed extraction method for FM fuze

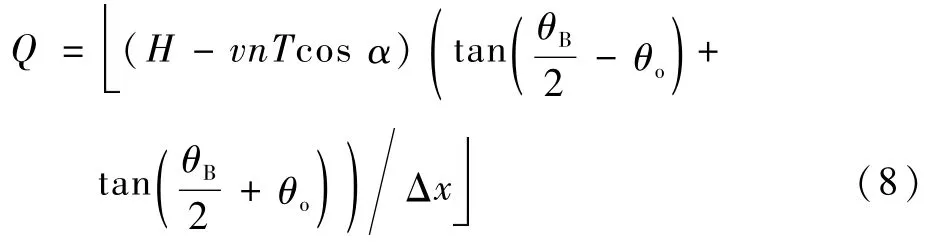
则第n+1个调制周期的差频信号为

式中：M为一个调制周期内采样的点数。

把每个周期的差频信号sIF（m，n，q）作为列向量，取N个周期的差频信号依次排列，即得到一个M×N的矩阵sIF（m，n，q）。对此矩阵做二维离散傅里叶变换：

由式（10）可以看出，粗糙面散射使得距离对应的差频频率和速度对应的多普勒频率存在更多分量，造成差频频率和多普勒频率都存在展宽，同时也造成了距离和速度的耦合。为了加快运算速度，二维距离-速度提取方法可以采用二维快速傅里叶变换（FFT）实现，而为了进一步细化频谱，更好地提取目标特性，可以采用补零二维FFT。

3 仿真与讨论

3.1 模拟点目标DRFM 干扰建模与仿真

考虑对地调频引信的理想情况，若地面目标为理想导体平面，引信天线波束中心与地面垂直，则地面反射为镜面反射，目标可等效为位于引信正下方的点目标，其到引信的距离为引信实际高度的2倍。在此条件下，对引信目标特性进行仿真，设引信在t=0时刻弹目距离为R=20 m，弹目相对速度为vr=500 m/s；引信发射信号为锯齿波调频信号，载频为3 GHz，调制频偏为50 MHz，调频为100 k Hz，仿真200个调频周期，在这一段时间内弹目接近了1 m，在炸高较高时对引战配合影响不大。使用MATLAB对点目标作用下引信差频信号进行仿真，并对差频信号进行二维补零FFT，提取目标二维频率特性，仿真结果如图3所示。

图3 点目标作用下调频引信差频频率与多普勒频率分布Fig.3 Beat frequency and Doppler frequency distribution of FM fuze under action of point target

对于点目标或完全模拟点目标的DRFM 干扰，调频引信的差频频率和多普勒频率都近似为点频，因此对差频信号进行采样相当于乘以宽度为T的矩形窗，对其进行FFT后其频谱有近似的sinc包络，包络的主瓣宽度为2/T，本文选取差频频谱和多普勒频谱主瓣-10 dB带宽作为差频频率和多普勒频率峰值带宽。

从仿真结果可以看出，点目标作用下调频引信差频二维频率分布近似为一个点，差频频率分布是二维频率分布的横坐标投影，多普勒频率分布是二维频率分布的纵坐标投影；差频频率峰值带宽为150 k Hz，多普勒频率峰值带宽不足1 k Hz；差频频率在650 kHz处出现最大值，多普勒频率在10.06 k Hz处出现最大值。弹目距离20 m对应差频频率理论值为666.7 kHz，相对速度500 m/s对应多普勒频率理论值为10 k Hz，由于实际差频频率等于距离差频减去多普勒频率，差频频率出现了10 kHz的偏移。因此，仿真频率最大值基本对应仿真设置的距离和速度，仿真结果表明，二维距离-速度提取方法可以提取目标的距离和速度信息。

对于完全模拟点目标回波的DRFM 干扰信号，调频引信二维频率分布等效于点目标，因此可以使用点目标仿真代替模拟点目标DRFM干扰。

3.2 粗糙面目标建模与仿真

根据瑞利准则，只有地面起伏远小于引信工作波长时，地面反射才可近似为镜面反射。而对于工作在S波段的调频引信来说，地面起伏通常可与波长比拟，甚至大于波长。因此，粗糙面目标作用下调频引信目标特性更接近实际战场的情况。

本文采用高斯粗糙面模拟粗糙地面，这里选取一维高斯粗糙面。高斯分布的功率谱密度为

式中：δ为高斯分布的标准差；L为表面相关长度。

仿真生成的高斯粗糙面局部如图4所示。

以高斯粗糙面作为模拟地面目标，建立引信弹目交会模型。为了更符合实际情况，假设引信天线3 dB波束宽度为θB=60°，天线波束中心与垂直方向夹角为15°，天线方向性函数为高斯函数：

其他仿真参数与点目标一致，对调频引信粗糙面目标特性进行仿真，对差频信号进行二维补零FFT，单次仿真的结果如图5所示。

从单次仿真的结果可以看出，与点目标作用下二维频率分布不同，粗糙面目标作用下调频引信二维频率分布存在一定随机性；差频频率峰值带宽为182.8 kHz，多普勒频率峰值带宽约为4 k Hz；差频频率和多普勒频率都出现了明显的展宽，峰值点也都出现了一定程度的偏移。由于每次仿真程序生成的随机粗糙面都不一样，所以每次仿真得到的结果也不太一样，对粗糙面目标特性进行100次仿真，对其结果取平均，得到仿真结果如图6所示。

经过100次仿真对其结果取平均，可以得到粗糙面作用下调频引信差频信号的二维频率分布范围，可以看出，粗糙面目标作用下差频频率和多普勒频率均出现展宽，多普勒频率展宽更为明显，其高频处能量相对较高；同时出现了距离和速度的耦合，造成差频频率和多普勒频率峰值点偏移。

3.3 讨 论

为了探讨调频引信的载频对粗糙面作用下差频的二维频率分布的影响，对粗糙面作用下不同频段的调频引信差频频率与多普勒频率分布进行了仿真，结果如图7和图8所示。

图7和图8中，仿真的引信载频分别为10、24 GHz，差频频率峰值带宽分别为 217.2、875 kHz，多普勒频率峰值带宽分别为12、30 kHz。仿真生成的粗糙面起伏度相同，由仿真结果可以看出，随着引信载频的增加，粗糙面目标作用下引信多普勒频率峰值带宽也随之增加，带宽大致与载频成正比。差频频率峰值带宽的展宽不明显，对比不同波段仿真结果可知，载频对差频频率峰值带宽影响较小。K波段由于多普勒频率较高，将仿真的调频提高到了400 k Hz，可以看出，差频频率峰值带宽也相应成倍数增加，与3.1节分析一致。

为了研究引信天线照射范围内粗糙面区域大小对差频频率峰值带宽和多普勒频率峰值带宽的影响，对不同高度处调频引信的差频二维频率分布进行多组仿真，得到差频频率峰值带宽和多普勒频率峰值带宽的平均值随高度变化的规律，如图9所示。可以看出，差频频率峰值带宽和多普勒频率峰值带宽均随着高度的降低和天线照射范围内粗糙面区域变小而降低，同时由于引信照射到的区域只是高斯粗糙面的局部，其高度起伏也存在差异，导致带宽随高度的变化出现波动。由仿真可以看出，引信天线照射范围内粗糙面的高度起伏造成调频引信差频频带和多普勒频带展宽，天线照射范围内粗糙面的大小影响了差频频率峰值带宽和多普勒频率峰值带宽，同时，多普勒频率峰值带宽还随着引信载频变化而变化，其大致与载频成正比。

图6 随机粗糙面目标作用下调频引信差频频率与多普勒频率分布（100次仿真）Fig.6 Beat frequency and Doppler frequency distribution of FM fuze under action of random rough surface target（100 simulations）

为了验证地面目标的多普勒展宽特性，基于收发共用天线的X波段调频多普勒引信样机，分别测试了针对点目标与土地目标的滑弹试验，滑弹高度60 m，入射角45°，弹速15～30 m/s。则调频谐波定距的多普勒包络信号输出波形分别如图10与图11所示。对比分析图10与图11可知，点目标作用下多普勒频率近似为点频情况，粗糙面作用下调频引信多普勒输出信号频域存在明显展宽，且频带内高频处能量较高，实测多普勒输出频域波形与仿真得到的频率分布一致，验证了粗糙面目标建模的正确性。

而后进行了基于双通道调频谐波定距的调频多普勒引信多延时叠加DRFM干扰对抗试验，试验测试结果如图12所示。可知，如果仅采用双通道谐波多普勒定距的方式，基于点目标模拟的DRFM干扰可有效干扰引信。

针对以调频引信差频频率峰值带宽和多普勒频率峰值带宽2个特征参量区分干扰与目标信号的验证，使用Wilcoxon秩和非参数假设检验来验证。Wilcoxon秩和检验又被称为Mann-Whitney秩和检验，是一种适用于两样本的非参数假设检验。Wilcoxon秩和检验计算后返回P值，P值越小，表示两样本分布差异越显著。使用蒙特卡罗方法仿真100组调频引信在随机粗糙面和模拟点目标DRFM干扰作用下的二维频率分布，Wilcoxon秩和检验得到统计箱型图如图13所示。可以明显看出，随机粗糙面作用下调频引信差频频率峰值带宽和多普勒频率峰值带宽都分布在一定区间内，而模拟点目标DRFM干扰作用下引信差频频率峰值带宽和多普勒频率峰值带宽分布非常集中，几乎是固定值。

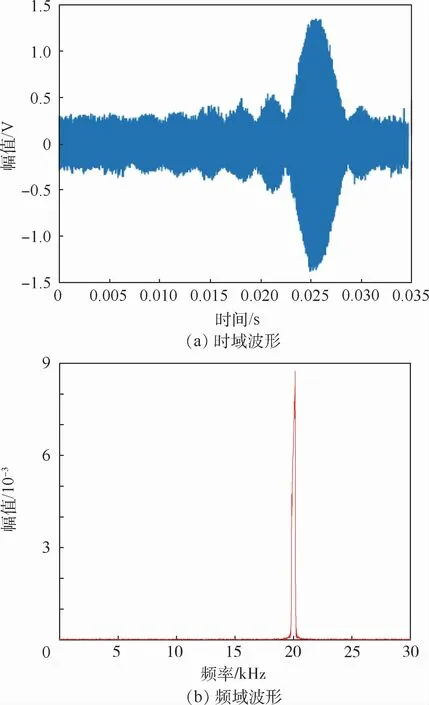
图10 点目标作用下调频引信多普勒输出波形Fig.10 FM fuze Doppler output waveform under action of point target

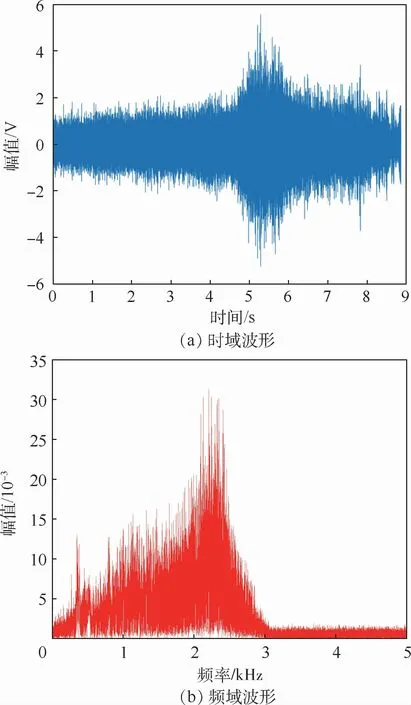
图11 土地目标作用下调频引信多普勒输出波形Fig.11 FM fuze Doppler output waveform under action of earth target

使用Wilcoxon方法计算得到差频频率峰值带宽PB=1.8265×10-26，多普勒频率峰值带宽PD=5.483 8×10-39。计算结果表明，粗糙面目标和模拟点目标DRFM 干扰作用下引信差频频率峰值带宽和多普勒频率峰值带宽差异极为显著，可有效区分粗糙面目标和模拟点目标的DRFM干扰信号。

4 结 论

1）粗糙面目标作用下，调频引信差频频率峰值带宽和多普勒频率峰值带宽展宽的幅度与引信天线照射范围内粗糙面的大小呈正相关，粗糙面高度起伏造成展宽量出现随机的波动。

2）粗糙面目标作用下，调频引信多普勒频率展宽更为明显，其高频处能量相对较高，峰值带宽展宽幅度与载频成正比，实测引信多普勒频域波形与仿真多普勒频率分布一致。

3）蒙特卡罗仿真和非参数假设检验计算表明，利用差频频率峰值带宽和多普勒频率峰值带宽特征可有效区分粗糙面目标和模拟点目标的DRFM干扰信号。