基于自适应遗传算法的MEMS加速度计快速标定方法
2019-11-21高爽张若愚
高爽,张若愚
(北京航空航天大学 仪器科学与光电工程学院,北京100083)
作为惯性测量系统的核心元件,微惯性测量单元(MIMU)是微机电系统(MEMS)的一个重要分支,具有体积小、成本低、质量轻、功耗低和耐冲击性等优点,在普通民用和战略军用导航等领域具有广阔的应用前景[1]。然而,在实际应用中,由于MEMS器件误差及系统误差受惯性测量单元的结构设计、外部环境等因素影响较大,MEMS惯性器件的精度成为制约MIMU导航性能的主要技术瓶颈之一。因此,MIMU的标定补偿成为低精度惯性导航领域的一大研究热点[2]。
分立式标定方法操作复杂,步骤繁琐,标定精度主要由转台精度决定。由于MIMU标定精度要求低、大批量生产等特点,需寻求简单易行的快速标定方法。为克服传统标定方法的弊端,Lötters等[3]首次提出基于模观测的加速度计标定方法,将标定问题转化为优化问题。在模观测标定中,研究关键在于非线性方程组的求解,其中,最常用的方法是迭代算法。Frosio等[4]采用牛顿迭代法求解非线性方程组,实现MEMS加速度计的外场自动标定,标定精度比传统标定方法提升一个数量级;Won和Golnaraghi[5]应用非线性最小二乘法进行迭代计算,在获得待标定参数的前提下降低了运算时间;Fong等[6]将下山单纯形算法应用于最小化目标函数,为加速度计的免转台标定提供了理论基础。然而,迭代算法存在的问题是求解过程复杂,初始值选取的优劣直接影响其收敛性和迭代结果。针对迭代算法存在的不足,基于迭代思想的智能算法以其在优化求解中的适用性、鲁棒性等突出优势,为标定优化问题提供了一种新思路。戴邵武等[7]采用粒子群优化(PSO)算法对加速度计进行快速标定,但未进行标定方法的现场试验验证;杨管金子等[8]利用遗传算法(GA)完成加速度计的免转台标定,但未实现对安装误差参数的标定。
针对以上问题,在不依赖转台的前提下,本文提出了一种基于自适应遗传算法的MEMS加速度计快速标定方法。实验结果表明,该方法能快速准确标定出全部误差参数,缩短标定时间,提高标定精度,且标定后能达到与传统标定方法相同量级的姿态精度。
1 加速度计标定模型
1.1 加速度计输出模型
在实际应用中,由于工作原理、制造工艺及使用环境等因素的影响,MIMU测量的输出信息通常会含有误差,测量输出应根据输入加速度信息和误差项建立数学模型。MIMU中加速度计的输出误差模型为
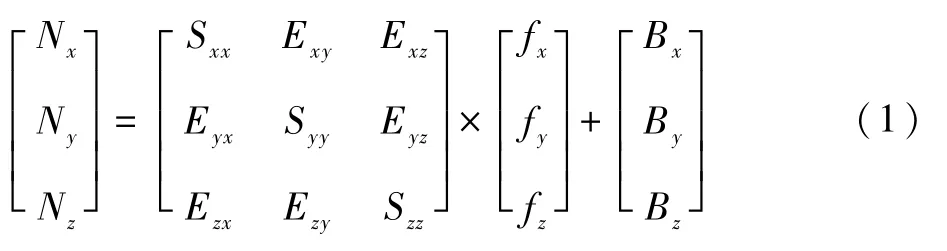
式中:[NxNyNz]T为加速度计的测量输出;[fxfyfz]T为 加 速 度 计 的 实 际 输 入;[BxByBz]T为加速度计的常值零偏;Sii(i=x,y,z)为加速度计的标度因数;Eij=Sii·Mij(i,j=x,y,z),Mij为加速度计的安装误差。
根据式(1)加速度计的输入输出关系,将加速度计的零偏、标度因数和安装误差进行补偿后,可得载体的实际加速度。补偿后的加速度计输出模型为

1.2 模观测标定原理
在静止状态下,加速度计的测量输出满足:

对式(3)两侧分别取模值:

在静止状态下,加速度计测量输出的模总是等于当地重力加速度的模,与加速度计的姿态无关[9]。因此,以加速度计测量输出的模为观测量,可实现对加速度计误差参数的标定。
根据模观测原理,将补偿后的加速度计输出模型代入式(4)后取平方得
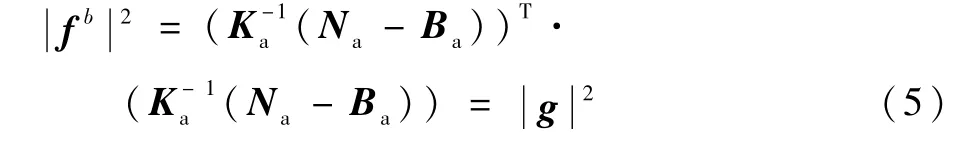
式中:Ka、Na、Ba分别与式(1)中元素相对应,Ka为标度因数和安装误差矩阵,Na为测量输出矩阵,Ba为零偏矩阵。
式(5)为单位置下加速度计的非线性输出方程。为求解标定参数,需对多位置下的测量输出进行观测,即联立非线性方程组。然而,由于器件固有的噪声和外界环境干扰等因素,加速度计实际输出的模与重力加速度之间存在误差,非线性方程组可改写为误差函数的形式:

式中:θ=[KaBa]为待标定参数;N为测试位置数。
通过构造目标函数,以标定参数为状态量,可将非线性方程组的求解问题转化为非线性函数的优化问题,通过最小化目标函数实现对误差参数的标定。
2 基于自适应遗传算法的标定参数求解
遗传算法是一种借鉴生物界自然选择和遗传机制发展起来的随机搜索优化算法,基于适者生存的原则,通过模拟自然进化在种群内的优胜劣汰实现对最优解的搜索[10]。遗传算法以群体搜索和个体间的信息交换为准则,采用概率法随机寻优,以其并行性、鲁棒性及自适应性等突出优势被广泛应用于系统辨识、故障诊断、自动控制等领域中复杂优化问题的求解[11-13]。
基于遗传算法的全局搜索能力,本文将遗传算法应用于MEMS加速度计的快速标定,建立目标函数与遗传算法适应度函数的关系,在全局范围内搜索标定参数的最优解。随机产生初始种群开始最优解迭代搜索,对种群中的个体进行适应度计算,以最大适应度为标准,更新最优适应度和最优染色体,通过选择、交叉和变异等遗传操作生成下一代种群,进行当前种群的个体适应度计算。如此循环迭代,直至满足优化终止条件,获得最优个体。算法流程如图1所示。
2.1 初始种群与编码
以标定参数作为种群中的个体,根据加速度计输出模型反推出最优解的取值范围,形成初始搜索区间。为避免连续函数离散化的映射误差,减少编码解码的复杂运算,本文采用实数编码代替传统的二进制编码方法,在搜索区间内随机产生实数串数据生成初始种群,以该数据作为初始种群开始迭代[14]。
2.2 适应度计算
适应度函数又称为评价函数,是根据目标函数确定的判别种群中个体优劣性的评价标准[15]。式(6)是加速度计测量输出模值与当地重力加速度模值的误差函数,通过适当变换可得遗传算法的适应度函数为

式中:E(ij)(θ)为第i代种群中第j个个体对应的误差函数值。适应度函数F(ij)(θ)为该误差函数的倒数。最大适应度对应的个体作为当前种群的最优个体被保存下来,进入下一代种群继续寻优。
2.3 选择、交叉与变异
选择、交叉与变异等遗传操作能够有效增加种群多样性,避免算法陷入局部最优,提升全局搜索能力。选择操作根据个体的适应度从上一代种群中择优选择个体复制到下一代种群,通过选择过程,种群中的最优个体不断更新,体现了优胜劣汰的进化原则。本文采用均匀排序的选择方法,对种群中的个体适应度大小进行排序,分配各个个体被选择的概率,使适应度高的个体具有更高的存活概率。
交叉操作是遗传算法中的核心运算,通过模拟遗传学的杂交原理,将种群中的2个个体随机搭配,以交叉概率交换部分染色体形成新的个体,体现出信息交换的思想。变异操作将种群的每个个体以变异概率任意改变基因值,维持种群的多样性,抑制算法过早收敛。在传统遗传算法中,通常采用固定的交叉概率(Pc=0.4~0.99)和变异概率(Pm=0.000 1~0.1),在复杂优化问题中存在收敛速度慢及早熟现象等问题。本文采用自适应交叉和变异概率代替固定概率[16-17],根据个体适应度自动调整Pc和Pm以实现最优参数的选择,保证算法较强的全局搜索能力和收敛性能。
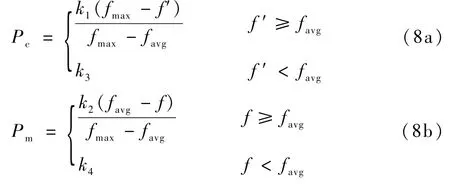
式中:fmax为当前种群的最大适应度值;favg为当前种群的平均适应度值;f′为交叉个体中较大的适应度值;f为变异个体的适应度值;常值参数取为k1=k3=1,k2=k4=0.5。
3 最优标定编排设计
由模观测原理可知,加速度计标定需通过观测多位置下的测量输出实现,测试位置的选择通常根据标定参数的数量和特点来确定。针对多位置标定方法,不同的路径编排导致加速度计的输入激励不同,合理的标定路径要求充分激励所有误差参数,且需要保证标定结果的唯一性。将标定参数作为状态变量,分析不同位置下加速度计测量输出对状态变量的可观测度,确定出最优的静态位置编排,保证标定路径的合理性[18]。
由于加速度计在静态位置下的测量输出不随时间变化而改变,则离散化时不变系统模型为

式中:X为状态变量;Y为观测输出;A和H 分别为系统状态矩阵和观测矩阵。
线性时不变系统的可观测性判别矩阵为
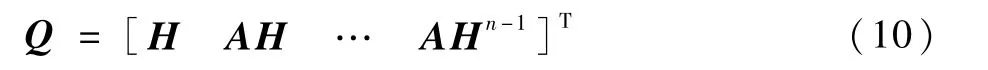
若满足rank(Q)=n,则系统完全可观测,否则系统存在不可观测量。
针对加速度计的静态误差模型,由于模观测标定方法无转台坐标系基准,安装误差矩阵只包含3项误差参数,本文以Mxy、Mxz、Myz作为待标定的安装误差。选取9项标定参数为状态变量:
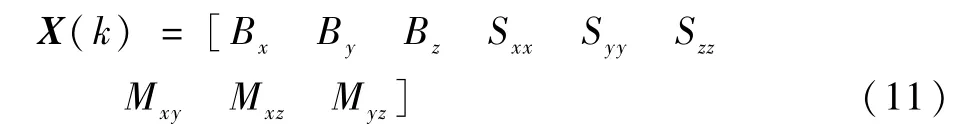
系统的状态变量为不随时间变化的确定值,其状态矩阵为

系统的观测输出能够反映不同位置下的输入激励,维数与标定方案的位置数目有关,其观测矩阵为

式中:I11,I21,…,IN1为3维单位阵;G12,G22,…,GN2为对应位置下重力加速度的输入激励矩阵。
根据奇异值分解理论,对系统可观测性判别矩阵Q进行奇异值分解:


为了分析矩阵Q奇异值和状态变量之间的关系,设正定对称矩阵M=QTQ,其特征值和特征向量分别为λi和wi,则特征值和特征向量之间的关系为

由式(15)可知,矩阵M 的特征值越大,其特征向量对应状态变量的可观测度越高,通过多位置下的系统可观测度分析,可得最大奇异值对应的位置对状态变量具有最高的可观测度,由此确定出最优位置编排。根据标定参数的数量和特点设计静态位置编排方案,如图2所示,多位置下可观测性判别矩阵的秩和奇异值如表1所示。

图2 静态多位置标定编排方案Fig.2 Static multi-position calibration scheme

位置 秩 奇异值3 8 29.861 29.713 29.562 29.405 29.405 29.405 4.220 2.969 1.715×10-7 4 9 41.585 41.585 41.585 29.716 29.562 29.405 6 5.168 4.198 5 9 41.585 41.585 41.585 41.585 41.585 29.564 6.708 6.708 5.968 6 9 41.805 41.585 41.585 41.585 41.585 41.585 7.348 4 7.348 4 5.968 3 7 9 51.106 46.513 41.693 41.585 41.585 41.585 7.937 2 7.819 6 6.006 3 8 9 55.280 46.533 46.513 46.493 46.493 41.657 8.374 9 8.263 3 6.033 1 9 9 59.063 55.107 50.992 46.596 46.493 46.493 8.649 9 8.394 6 6.451 9 10 9 64.408 57.427 50.991 48.495 48.261 46.572 9.154 2 9.122 3 8.204 8 11 9 68.476 58.829 55.023 50.931 50.931 47.303 9.882 8 9.8328 9.463 6 12 9 72.041 65.751 58.810 51.012 50.931 50.931 10.392 10.392 9.881 7 13 9 72.041 67.576 58.813 58.810 52.764 50.951 10.816 10.765 10.605 14 9 72.041 68.973 62.385 62.377 55.011 55.011 11.178 11.149 11.132 15 9 72.041 68.973 65.779 62.394 62.394 62.377 11.458 11.456 11.439
由表1可知,当N≥4时,矩阵满秩,系统完全可观测;当N≥7时,各项奇异值明显增大,这是由于与加速度计敏感轴成45°的位置使得系统可观测度增强;当N≥12时,最大奇异值不再增大,且其他各项奇异值的增幅较小。综合分析标定精度和标定复杂度等因素,本文选取12位置的静态多位置标定方案。
4 实验结果分析
本文以Xsens公司惯性导航系统MTi-1系列为测试对象,其结构如图3所示。根据第3节所述标定路径,在大理石平台上对MTi-1进行位置翻转实验,每个位置静止1 min,采集传感器数据,再翻转至下一位置。
完成数据采集后,采用本文方法对加速度计的标定参数进行最优化求解,遗传算法的适应度函数变化曲线及加速度计误差参数标定结果如图4和图5所示。
由图4可知,最优适应度能够准确跟踪平均适应度的变化。进化初期保持较小的适应度,以提高种群的全局搜索能力;进化后期适应度增大,快速收敛至全局最优解。由图5可知,通过自适应遗传算法的迭代搜索,标定参数全部实现收敛。由此可见,自适应遗传算法能够较好地应用于MEMS加速度计的标定问题。
为了验证本文方法的优越性,以传统多位置法的标定结果作为标定真值,将本文方法与牛顿迭代法进行对比,2种方法的标定结果如表2和表3所示。

图3 MTi-1系列惯性测量组合Fig.3 MTi-1 series inertial measurement unit
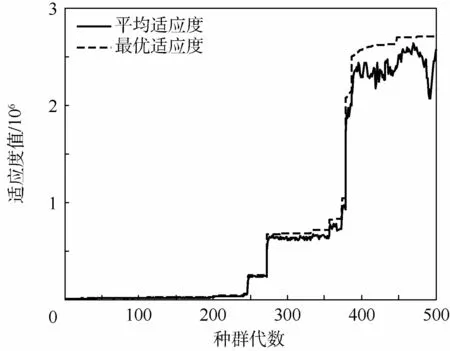
图4 适应度函数变化曲线Fig.4 Curves of fitness function variation
由表2可知,在牛顿迭代法的标定结果中,三轴零偏的相对误差分别为-0.146%、-0.554%、1.451%,三轴标度因数相对误差分别为0.000 204%、0.010 4%、0.414%,未能有效标定安装误差;在本文方法的标定结果中,三轴零偏的相对误差分别为-0.017%、0.019%、-0.051%,三轴标度因数相对误差分别为 0.007%、0.004%、0.000 3%,三轴安装误差的相对误差分别为10.69%、53.64%、21.37%,标定精度比牛顿迭代法提升1~3个数量级。由表3可知,本文方法的运算速度比牛顿迭代法提升61%。
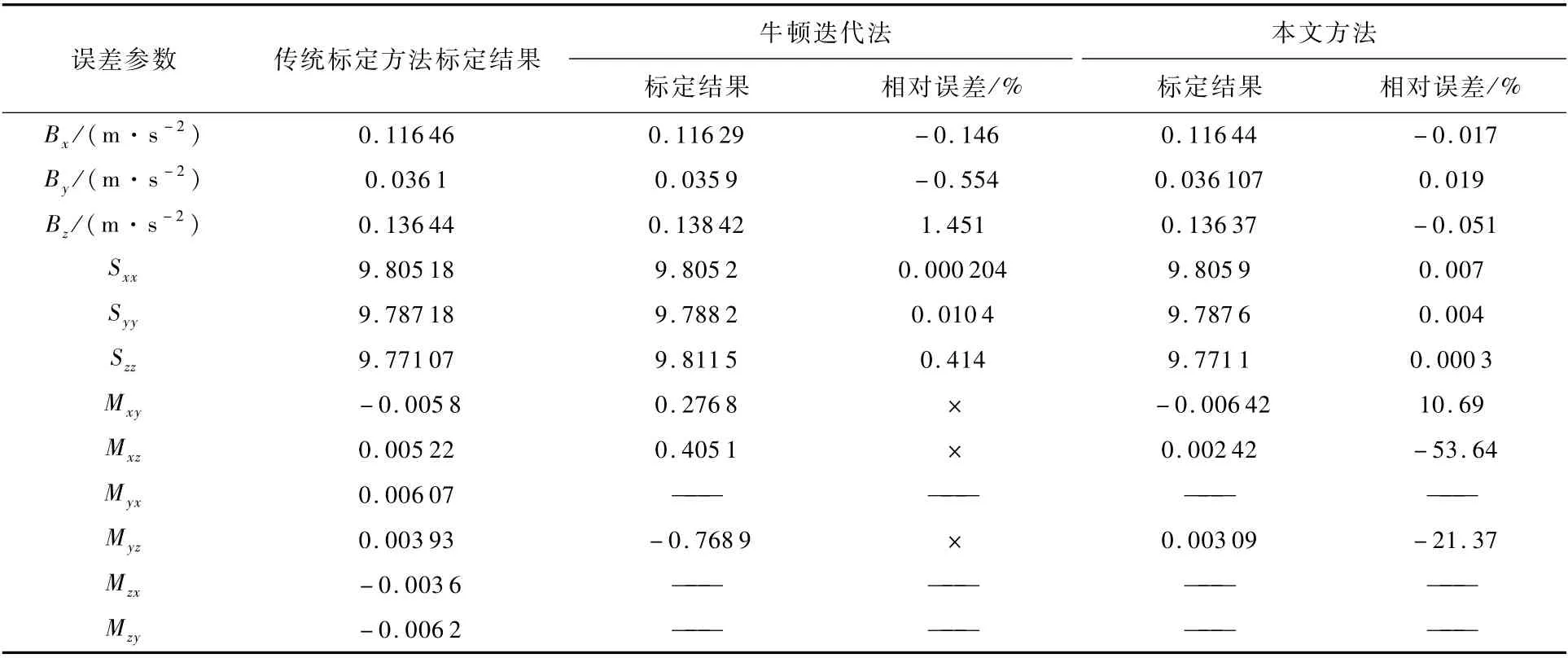
误差参数 传统标定方法标定结果牛顿迭代法 本文方法标定结果 相对误差/% 标定结果 相对误差/%Bx/(m·s-2)0.116 46 0.116 29 -0.146 0.116 44 -0.017 By/(m·s-2) 0.036 1 0.035 9 -0.554 0.036 107 0.019 Bz/(m·s-2) 0.136 44 0.138 42 1.451 0.136 37 -0.051 Sxx 9.805 18 9.805 2 0.000 204 9.805 9 0.007 Syy 9.787 18 9.7882 0.0104 9.7876 0.004 Szz 9.771 07 9.811 5 0.414 9.771 1 0.000 3 Mxy-0.005 8 0.276 8×-0.006 42 10.69 Mxz 0.005 22 0.4051×0.002 42-53.64 Myx 0.006 07 —— —— —— ——Myz 0.003 93-0.768 9×0.003 09-21.37 Mzx -0.003 6 —— —— —— ——Mzy -0.0062—— —— —— ——

方法 运算时间/s本文方法164.28牛顿迭代法421.92
在静态条件下,将传统标定方法、牛顿迭代法与本文方法分别应用于MTi-1惯性导航系统,开展纯惯性导航验证实验,不同方法下的水平姿态角误差曲线及误差均值如图6和表4所示。
由图6和表4可知,本文方法标定后的俯仰角误差约为0.062°,相较于牛顿迭代法减小74%,与传统标定方法精度相当;本文方法标定后的横滚角误差约为-0.051°,精度优于牛顿迭代法和传统标定方法。
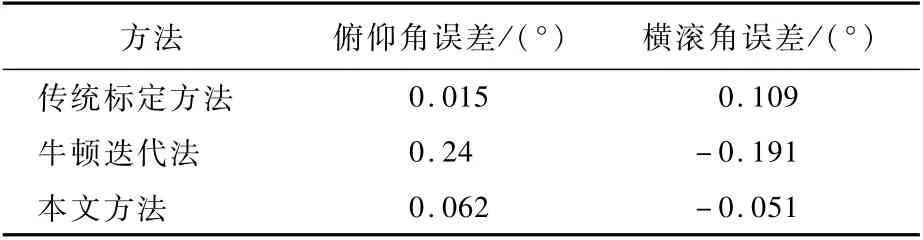
方法 俯仰角误差/(°) 横滚角误差/(°)0.015 0.109牛顿迭代法 0.24 -0.191本文方法传统标定方法0.062 -0.051
结合不同方法的标定结果与导航实验结果,可以得出本文方法的优势如下:
1)能够准确标定出MEMS加速度计的全部误差参数,与牛顿迭代法相比,标定精度提升1~3个数量级,运算速度提升61%,本文方法可有效应用于MEMS加速度计的快速标定。
2)标定后解算的水平姿态角误差小于0.1°,能达到与传统标定方法相同量级的精度,验证了本文方法在实际导航中的应用价值。
5 结 论
1)本文针对传统标定方法标定时间长、标定精度依赖转台精度等问题,提出了一种基于自适应遗传算法的MEMS加速度计快速标定方法,实现对全部误差参数的快速准确标定。根据模观测原理,将标定问题转化为非线性方程组的优化求解问题;以系统可观测性分析为依据,设计最优标定路径。采用自适应交叉和变异概率,提升遗传算法的全局搜索和收敛性能。
2)实际测试结果表明,与牛顿迭代法相比,本文方法具有标定精度高、标定速度快等优点,标定后能达到与传统标定方法相同量级的姿态精度,验证了本文方法的优越性和有效性。
3)本文方法缩短标定时间,降低标定成本,具有重要的理论研究和工程应用价值。同时,由于遗传算法的参数选取直接影响标定精度及运算速度,如何通过适应度函数的动态变化及对选择、交叉、变异算子的改进以提升遗传算法的寻优精度和收敛速度是未来工作中值得进一步研究的问题。
