动力学自然单元法的谐波激励下的连续体结构拓扑优化
2019-11-20徐家琪马永其
徐家琪,马永其,2
(1.上海大学 上海市应用数学与力学研究所,上海 200072;2.上海大学 力学系,上海 200444)
结构拓扑优化的源头可追溯至20世纪初Michell等[1]提出的应力约束下具有最小重量桁架的结构优化,它的出现使人们摆脱了原有依靠经验获得最优结构的思维模式,开始依靠理论计算获得经济且实用的结构。连续体结构拓扑优化是在不知道结构拓扑形状的前提下,根据已知边界条件和荷载条件确定比较合理的结构拓扑形式,与离散体结构拓扑优化相比,设计变量多,模型复杂。自1988年Bendsøe等[2]提出了均匀化方法(Homogenization Method)开启连续体结构拓扑优化研究以来,针对连续体结构拓扑优化的研究逐渐广泛和深入。Bendsøe等[3]在先前研究的基础上提出了变密度法,Sui等[4]提出了独立连续映射法(Independent Continuous Mapping,ICM),Xie等[5]提出了渐进结构优化法(Evolutionary Structure Optimization,ESO)等用来进行实现连续体结构拓扑优化的计算。
研究连续体的结构拓扑优化除了集中在静力学领域以外,不少学者也进行了动力学领域的研究,主要包括两个方面,一是以特征频率作为目标函数或是约束条件的结构拓扑优化。如Xie等[6]采用ESO方法以特征频率作为约束条件进行结构拓扑优化;邱海等[7]对具有频率约束的板结构进行了拓扑优化研究;Díaaz等[8]采用均匀化方法以结构特征频率最大化为目标函数进行了结构拓扑优化;Pedersen[9]采用变密度法以结构特征频率最大化为目标函数进行了结构拓扑优化。魏星等[10]基于自然单元法,研究了功能梯度板频率优化。问题二是在动载荷作用下,以结构柔度为目标函数的结构拓扑优化。如Ma等[11]基于均匀化方法研究了结构受激励载荷的动态响应问题,Jog等[12]定义了结构的动力学柔度研究了带有周期载荷的结构拓扑优化,徐斌等[13]采用ESO方法研究了频率激励载荷下薄板的结构拓扑优化。刘虎等[14]将结构指定位置稳态阶段位移响应幅值作为目标函数,研究了简谐力激励下结构拓扑优化问题。
大多数的连续体结构拓扑优化计算都是基于有限元方法进行的,由于有限元方法本身对网格的依赖性,网格划分、网格数量和形式都会对连续体结构拓扑优化结果产生极大影响,且会使优化结果产生棋盘格现象[15]。因此避免棋盘格现象的产生,同时提高计算精度与计算效率是目前主要的研究方向[16-18]。
近年来,随着无网格方法的兴起,人们开始采用无网格方法取代有限元方法以避免优化过程中棋盘格现象的产生。目前,已经发展的无网格方法有十几种,主要包括光滑粒子法[19],无单元Galerkin方法[20](EFG),重构核粒子法[21],无网格点插值法[22](PIM),自然单元法[23](NEM)等。Zhou等[24]采用了重构核粒子法对连续体结构进行了静力学拓扑优化研究。Zheng等[25-26]采用无单元Galerkin方法以及径向点插值法分别进行了静力学连续体结构拓扑优化研究。Wu等[27]将改进的无单元Galerkin方法应用于连续体拓扑优化。在动力学连续体结构拓扑优化研究方面,郑娟等[28-29]采用无网格径向插值点法、无单元Garlerkin方法,进行了频率激励载荷下连续体结构拓扑优化的研究,使优化结果避免棋盘格现象的产生。但是提高计算精度与计算效率依然是人们努力研究的方向。大部分无网格方法相关的形函数不满足Delta性质,不能直接施加本证边界条件,必须通过增加Lagrange乘子法、罚函数方法等附加计算,才能施加本证边界条件,不可避免地增加了计算成本,影响计算效率。自然单元法是基于Voronoi图和Delaunay三角形概念进行插值的无网格方法,其形函数简单,计算效率高,边界上满足Delta插值性质,可以直接施加本征边界条件,避免增加附加计算成本。
本文利用自然单元法求解效率高的特点,将动力学自然单元法应用于频率激励载荷作用下的连续体结构拓扑优化计算,以节点密度作为设计变量,结构动柔度最小作为目标函数,施加体积约束,采用基于变密度法的各向同性固体微结构惩罚模型(Solid Isotropic Microstructure with Penalization,SIMP),建立拓扑优化模型并采用优化准则法(OC)求解优化模型,在避免棋盘格现象产生的同时提高计算的效率和精度,并通过算例说明该方法的有效性和优越性。
1 动力学问题自然单元法
1.1 Voronoi图与Delaunay结构
自然单元法(Natural Element method,NEM)是基于Voronoi图及其对偶图形Delaunay三角剖分来建立插值函数的。
在二维空间R2中分布着一系列点所组成的点集S={x1,x2,…,xn}。点xi的Voronoi晶胞定义为Pi。当d(x,xi)代表空间中任意一点到xi的距离时,Pi可定义为
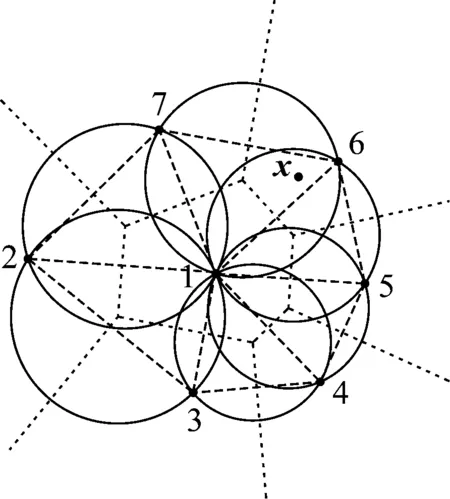
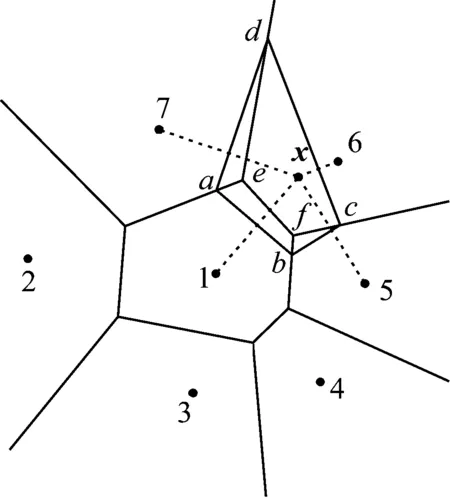
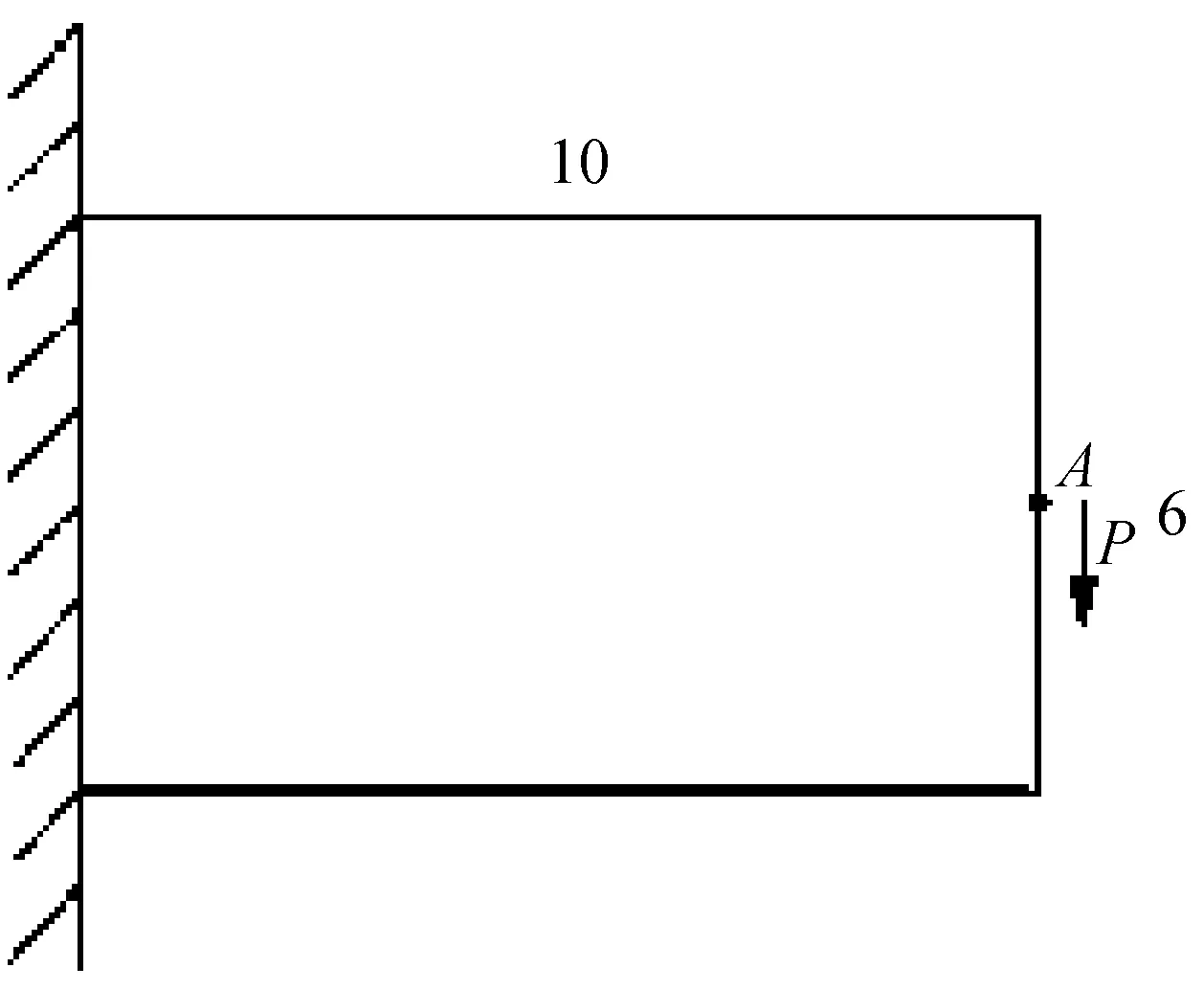
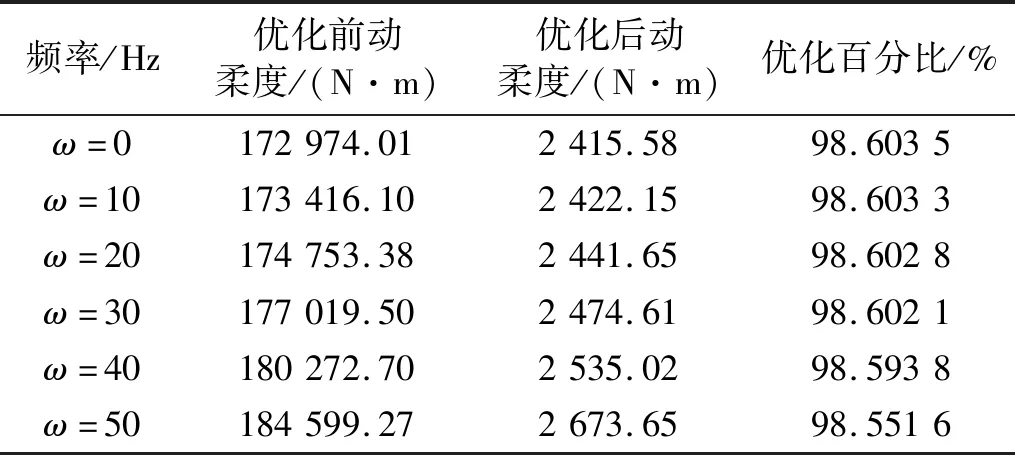
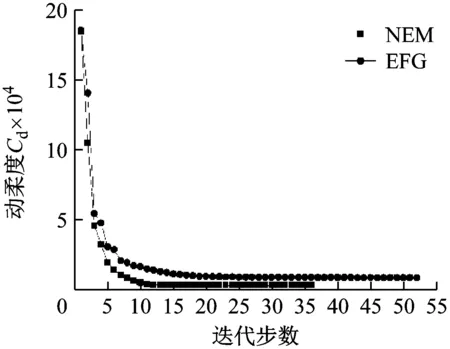
Pi={x∈R2|d(x,xi) (1) 如图1所示为包含7个点的Voronoi图。将Voronoi图中拥有公共边的两个晶胞所对应的节点相连结,就可以构成Delaunay三角剖分图。与一般的三角剖分不同的是,Delaunay三角形具有空外接圆以及最大化最小角的特性。该特性为寻找插值点自然邻点,建立插值函数提供了依据。绘制Delaunay三角形的外接圆,并找出外接圆的圆心,如图2所示,此时Delaunay三角形的外接圆圆心即为Voronoi晶胞的顶点。 图1 带有7节点Vornonoi图Fig.1 Voronoi diagram with seven nodes 图2 Delaunay三角形外接圆Fig.2 Natural neighbor circumcircles 如图3所示,若点x为插值点,该点位于点1,6,7和点1,5,6组成的两个三角形的外接圆中,则称点1,5,6,7为插值点x的自然邻点。插值点x的二阶Voronoi晶胞如图4所示。确定插值点的自然邻点之后,即可构造插值函数式(2) (2) 式中:h(x)为插值点的物理量N为插值点的自然邻点的个数;hI为插值点的第I个自然邻点的物理量;φI为自然邻点I所对应的形函数。形函数的构成方法可以分为Sibson插值和non-Sibson插值。其中Sibson插值方法为 (3) (4) 插值点x关于第1个自然邻点的形函数则可表示为 (5) 图3 插值点x的自然邻点Fig.3 Natural neighbor nodes of x 图4 插值点x的二阶Voronoi晶胞Fig.4 Second order Voronoi diagram of x 二维弹性动力学问题的平衡方程为 (6) (7) (8) (9) (10) (11) 式中:B为应变矩阵;D平面应力情况下的为弹性矩阵;ρm为质量密度;Φ为插值点所对应的形函数。令U(t)=UAeiwt,F(t)=FAeiwt,式(9)可表示为 KUAeiwt-ω2MUAeiwt=FAeiwt (12) 同时约去eiwt,则 (K-ω2M)UA=FA (13) 式中:ω为激励频率;UA为位移幅值;FA为频率激励载荷幅值。 SIMP模型的基本思想是将连续体假想为一种密度可变的材料,每个节点的相对密度可看作在0~1之间变化。对弹性矩阵及质量矩阵进行插值的SIMP模型为 D=ρPD0 (14) M=ρQM0 (15) 式中:P,Q分别为针对刚度矩阵和质量矩阵的惩罚因子。当相对密度ρ=1时,表示插值点具有实体材料,当相对密度ρ=0时,意味着该处没有材料存在。 对于惩罚因子P来说,上式矩阵D中包含材料杨氏模量E和泊松比μ。根据Hashin-Shtrikman上下限定理,材料的体积模量K和剪切模量G需满足下列不等式 (16) 式中:K0、G0分别为初始的体积模量和剪切模量。推导该不等式,可得出惩罚因子P的下限,与材料的泊松比μ有关。 (17) 对于惩罚因子Q,若其值小于P,在相对密度低的区域,刚度矩阵与质量矩阵的比值较小。为保证衰减的同步性,这里采用文献[28]的做法,采用相等的P和Q。 拓扑优化的目标函数设置为结构的动柔度最小,设计变量为节点相对密度,施加体积约束。拓扑优化的数值模型可表示为 (18) (19) (20) 求解优化模型涉及的目标函数以及约束的灵敏度,通过伴随分析法进行求解。 (21) 式中,A为任意实向量,此时,右边第二项为0。对上式求导为 (22) (23) (24) 结构的体积表示为式(25),结构体积的灵敏度表示为式(26)。 (25) (26) 考虑如图5所示的悬臂版,该板长为10 m,宽为6 m。右侧中点处加载一个竖直向下的频率激励载荷P=5eiwtkN,激励载荷幅值为5 kN。结构的弹性模量E为3×107Pa,泊松比μ为0.3,结构的质量密度为1 kg/m3,刚度矩阵以及质量矩阵的惩罚因子同时设置为4。将结构离散为25×15共375个节点,剖分出672个Delaunay三角形,如图6所示。在每个三角形内插入3个高斯积分点。设置体积约束为50%,收敛条件设置为设计变量的最大变化小于0.01。 图5 悬臂板结构Fig.5 The structure of cantilever plate 图6 悬臂板Delaunay三角剖分Fig.6 Delaunay triangles of cantilever plate 当频率为从0 Hz逐渐增加到40 Hz时的拓扑优化图形如图7所示,频率为50 Hz的拓扑优化图形如图9所示。当ω=0 Hz时,相当于静力学拓扑优化。激励频率不同,所获得的拓扑优化图形相似。将优化百分比定义为柔度减少量占原有柔度的比值,当激励频率增大时,优化前动柔度增大,优化后的动柔度也随之增大,目标函数变化如表1所示。当激励频率越小时,优化百分比越大,说明获得的优化结果越好。 (a)ω=0 Hz (b)ω=10 Hz (c)ω=20 Hz (d)ω=30 Hz (e)ω=40 Hz图7 不同频率激励载荷下悬臂板的拓扑优化结果Fig.7 Topology optimization results of cantilever plate under different frequencies 表1 不同频率下悬臂板目标函数值的优化结果Tab.1 Target function values of the cantilever plate at different frequencies 在结构参数,约束条件,收敛条件,节点数设置相同的情况下,分别采用无单元Galerkin方法(EFG)和自然单元法(NEM)进行激励频率ω=50 Hz时的结构拓扑优化。采用EFG进行计算时,在结构中分布40个背景积分网格,在每个积分网格中插入16个高斯积分点,影响域设置为1.5,以获相似的初始目标函数。所得的拓扑图形如图8、图9所示。两种计算方法的收敛曲线如图10所示。NEM优化单步耗时为24.26 s,结构动柔度由184 599减小到2 673。为EFG优化单步耗时为30.13 s,结构动柔度由185 303减小到8 250。从计算结果看,EFG和NEM方法获得的优化结果均无棋盘格现象出现,就优化效果来说,NEM方法图形较清晰,效果较好。从计算效率看,在初始动柔度相似的情况下,NEM单步耗时和总耗时均较少,说明自然单元法求解速度更快。 图8 EFG激励频率ω=50 Hz悬臂板拓扑优化结果Fig.8 Topology optimization result by using EFG(ω=50 Hz) 图9 NEM激励频率ω=50 Hz悬臂板拓扑优化结果Fig.9 Topology optimization result by using NEM(ω=50 Hz) 图10 NEM与EFG拓扑优化收敛图Fig.10 Optimization convergence curves of EFG and NEM 造成以上现象的原因主要是由于EFG的形函数较为复杂,背景积分网格独立于节点,积分网格的数量以及和排布方式对于计算结果影响较大,影响域的大小对计算结果以及计算速度也都会产生影响。而NEM的形函数计算较为简单,可以直接施加本征边界条件,计算时将结构自动划分为Delaunay三角形作为积分网格,三角形中分布高斯积分点后,高斯积分点依照Delaunay规则自动寻找自然邻点,排除了人为设置的影响域对计算结果的影响。 如图11所示简支板,长为10 m,宽为4 m,下边界中点处加载频率激励载荷P=5eiwtkN,激励幅值为5 kN。结构的弹性模量为3×107Pa,泊松比为0.3,结构的质量密度为1 kg/m3,刚度矩阵以及质量矩阵的惩罚因子同时设置为4。将结构离散为29×11共319个节点,并剖分成560个Delaunay三角形,如图12所示。在每个三角形内插入3个高斯积分点。设置体积约束为50%,收敛条件设置为设计变量的最大变化小于0.01。 图11 简支板结构Fig.11 Structure of simply supported plate 图12 简支板Delaunay三角形剖分Fig.12 Delaunay triangles of cantilever plate simply supported plate 如图13所示为ω为50 Hz时,简支梁的优化过程,在不断迭代的过程中,结构外形趋于光滑。在激励频率ω分别为50 Hz和100 Hz时,优化结果如图14、图15所示。 (a)第5步 (b)第10步 (c)第30步 (d)第50步 (e)第55步 (e)第60步图13 ω为50 Hz的拓扑优化过程Fig.13 Topology optimization process of simply supported plate(ω=50 Hz) 图14 激励频率ω为50 Hz拓扑优化结果Fig.14 Topology optimization result under ω=50 Hz 图15 激励频率ω为100 Hz拓扑优化结果Fig.15 Topology optimization result under ω=100 Hz 本文进行了频率激励作用下,基于动力学自然单元法的连续体结构拓扑优化计算。应用自然单元法,将结构离散成节点,并将所离散出的节点的相对密度作为设计变量,利用SIMP模型,建立动柔度最小化作为目标函数并施加体积约束的拓扑优化模型。采用伴随分析法计算结构的灵敏度,再利用优化准则法对模型进行求解。 通过对悬臂板频率激励下结构拓扑优化的计算表明,当激励频率不同时,得到了相似的拓扑优化图形。当激励频率增大,初始动柔度增大,优化结果的柔度也随之增大,优化百分比随之减小,说明频率激励较低时,可获得更好的优化效果。在初始动柔度相似的情况下,采用EFG和NEM方法分别进行拓扑优化,由于形函数构造方式简单,且可直接施加本征边界条件,相比于EFG方法,NEM显示出具有更高的计算效率。同时,采用NEM方法可获得更小的目标函数,说明该方法的优化效果更好。通过对受频率激励的简支板进行结构拓扑优化计算,表明随着迭代步数的增加,结构外形趋于光滑,最终获得了清晰的结构拓扑优化结果,进一步说明了该方法的可行性和有效性。 可以看出,动力学自然单元法进行频率激励下的结构拓扑优化计算,不仅可以克服有限元方法进行拓扑优化计算的网格依赖性以及拓扑优化中经常出现的棋盘格等数值不稳定现象,而且相比其它无网格方法,具有更高的计算效率,说明自然单元法应用于频率激励拓扑优化计算具有的可行性和优越性。

1.2 自然邻点插值
1.3 动力学问题的平衡方程

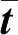
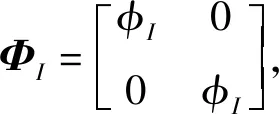
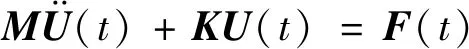

2 频率激励载荷拓扑优化
2.1 SIMP模型
2.2 拓扑优化模型
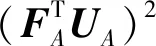


3 灵敏度分析
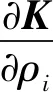
4 算 例
4.1 悬臂板








4.2 简支板










5 结 论
