反结构切换混沌系统

颜闽秀，徐 辉

(1.沈阳化工大学信息工程学院，辽宁 沈阳，110142；2.沈阳化工大学工业环境-资源协同控制与优化技术辽宁省高校重点实验室，辽宁 沈阳，110142)

切换混沌系统由多个子系统组合而成，与模型中只有一个非线性方程组的混沌系统相比，其具有更加复杂的动力学行为和更强的伪随机性，使得混沌同步保密通信的安全性能大大提高[1-3]。为了使多系统切换混沌同步技术在工程实际中得到更为广泛的应用，研究人员构建出不同结构的切换系统。文献[4]将Lorenz系统的第三个方程中的非线性项xy改为x2，同时引入线性反馈项x或y，得到4个混沌子系统来进行自动切换。文献[5]提出一个含有4个参数、2个非线性项的混沌系统，文献[6]则将该混沌系统模型中第三个方程的非线性项x2换成xy，得到一个新的子系统，并与原系统实现自动切换。文献[7]将Chen系统中第三个表达式的二次项分别换成x2、y2平方项得到两个子系统，并和Chen系统组成自动切换混沌系统。文献[8]是将文献[9]提出的模型中第三个方程含有的x2项换成xy和y2，得到两个新系统和原系统进行三个子系统的自动切换。

上述切换混沌系统都是在已有模型的基础上，将其中的二次项换成其他形式的二次项，通过改变系统的状态变量来得到可进行切换的子系统。

本文通过设计切换函数，提出一个新的非自治切换混沌系统，它具有两个互为反结构的子混沌系统[10]，仅仅通过改变模型表达式系数的正负号来实现两个子混沌系统的切换，减小了通过改变状态变量来实现切换的难度以及实际应用中搭建电路的复杂性。下面首先通过理论分析和仿真实验进行该系统的动力学特性分析，然后设计系统电路并利用Multisim模拟来验证所提出的新混沌系统的可实现性。

1 系统模型及其特性分析

在提出本文的反结构切换混沌系统之前，首先对两个子混沌系统A和B作简要分析。

1.1 子混沌系统A

子混沌系统A的模型为：

(1)

式中：系统参数a=4，b=12.5，c=3，d=2。现给定初始值(0.1，0.1，0.1)，利用Matlab仿真可得系统A的混沌吸引子，如图1所示。

(a)x-y-z三维相图 (b)x-y平面相图

(c)x-z平面相图 (d)y-z平面相图

图1 系统A的吸引子相图

Fig.1 Phase diagrams of attractors of system A

利用正交法求得系统A的李雅普诺夫指数为：λL11=0.6949，λL12=0，λL13=-3.6949。按式(2)计算系统的李雅普诺夫维数D1L：

(2)

式中：j为满足下式的最大整数,

(3)

故此处j取2，最终得到：

(4)

系统A的三个李雅普诺夫指数中，一个为正数，一个为零，另一个为负数，且它的李雅普诺夫维数为分数，所以可判断系统A是一个混沌系统。

1.2 子混沌系统B

子混沌系统B的模型为：

(5)

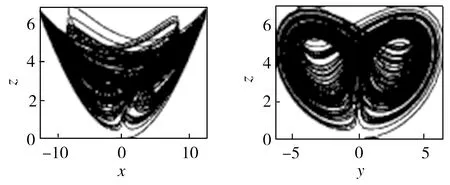
这里的参数a、b、c、d与混沌系统A的参数相同，不同的是二次项系数的符号与系统A的相反。给定初始值(0.1，0.1，0.1)，利用Matlab仿真可得系统B的混沌吸引子，如图2所示。

(a)x-y-z三维相图 (b)x-y平面相图

(c)x-z平面相图 (d)y-z平面相图

图2 系统B的吸引子相图

Fig.2 Phase diagrams of attractors of system B

求得系统B的李雅普诺夫指数为：λL21=0.6821，λL22=0，λL23=-3.6822。计算其李雅普诺夫维数为：

(6)

与系统A类似，可判断出系统B是一个混沌系统。

系统A和系统B互为反结构混沌系统，从图1和图2可以明显看出二者吸引子的不同，即它们正反颠倒。

下面通过设计简单的切换函数，将混沌系统A和B构建成一个切换混沌系统，称为反结构切换系统，并对反结构切换混沌系统的吸引子及其一般特性进行分析。

1.3 反结构切换混沌系统模型

本文提出的新型反结构切换混沌系统模型为：

(7)

式中：系统参数仍为a=4，b=12.5，c=3，d=2；f是所设计的切换函数，其表达式为：

(8)

图3 正弦函数和切换函数的图像

Fig.3 Graphs of sinusoidal function and switching function

切换函数f的功能就是通过改变系统模型二次项系数的符号来实现两个子系统的切换。从图3中可知：在第一个0.5T内f=1，切换混沌系统先以子系统A的模型运行；在第二个0.5T内f=-1，切换混沌系统以子系统B的模型运行。如此反复切换运行。

给定初始值(0.1，0.1，0.1)，利用Matlab仿真得到反结构切换系统(7)的吸引子，如图4所示。

(a)x-y-z三维相图 (b)x-y平面相图

(c)x-z平面相图 (d)y-z平面相图

图4 切换系统的吸引子相图

Fig.4 Phase diagrams of attractors of the switchable system

从图4可以清楚看出，切换系统的吸引子是有界的，其首先以系统A的模型运行，形成下半部分吸引子；当运行至半个周期结束时，下半部分吸引子产生一条连续的脱离轨迹线来切换至系统B，从而产生上半部分吸引子；当一个周期运行结束时，上半部分吸引子产生一条连续的脱离轨迹线来进行下一次切换运行。

1.4 切换系统的耗散性及其吸引子存在性

-a+c-d=-3

(9)

(10)

上式表明，当t趋于无穷时,包含系统轨迹的每个体积元均以指数级速率收缩到零，这证明了系统吸引子的存在性。

1.5 切换系统的混沌性

采用正交法得到切换系统的李雅普诺夫指数为：λ1=0.6963，λ2=0，λ3=-3.6784。时间变化时的李雅普诺夫指数谱如图5所示，可见随着时间的演化，系统的3个李雅普诺夫指数都趋于一固定常数。

根据式(2)得到反结构切换系统的李雅普诺夫维数DL=2.1893。该系统具有正、负、零三个李雅普诺夫指数，且李雅普诺夫维数为分数，可判定它是混沌系统。

图5 时间变化时的李雅普诺夫指数谱

Fig.5 Lyapunov exponential spectra with the variation of time

1.6 切换系统的平衡点及其稳定性

由于切换混沌系统是系统A和系统B经切换函数联结构成，所以它的平衡点也是由系统A和B的平衡点组成。

令系统A的模型式(1)等号左边为0，得到：

(11)

解得系统A的平衡点为：A1(0，0，0)，B1(-8.795，-2.814，-3.96)，C1(8.795，2.814，-3.96)。

在点A1(0，0，0)线性化得到Jacobian矩阵为：

(12)

解得其特征值为6.553、-2、-7.553，因其有两个负实根、一个正根，所以平衡点A1为系统的不稳定鞍点。采用类似方法可判定B1、C1点为系统的不稳定鞍焦点。

令系统B的模型式(5)等号左边为0，得到：

(13)

解得系统B的平衡点为：A2(-8.795，-2.814，3.96)，B2(0，0，0)，C2(8.795，2.814，3.96)。

在平衡点A2(-8.795，-2.814，3.96)线性化得到Jacobian矩阵为：

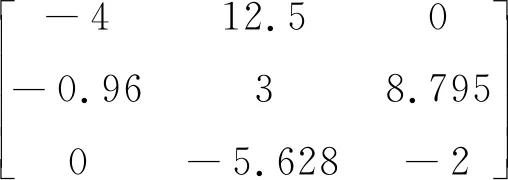
(14)

解得其特征值为0.3348-7.338i、0.3348+7.338i、-3.67，因其有一个负实根、两个实部为正的共轭复根，所以A2点为系统的不稳定鞍焦点。采用类似方法可判定B2点为系统的不稳定鞍点、C2点为系统的不稳定鞍焦点。

综上所述，系统的所有平衡点均是不稳定的。

1.7 切换系统关于的分岔图和李雅普诺夫指数谱

图6 参数变化时的分岔图

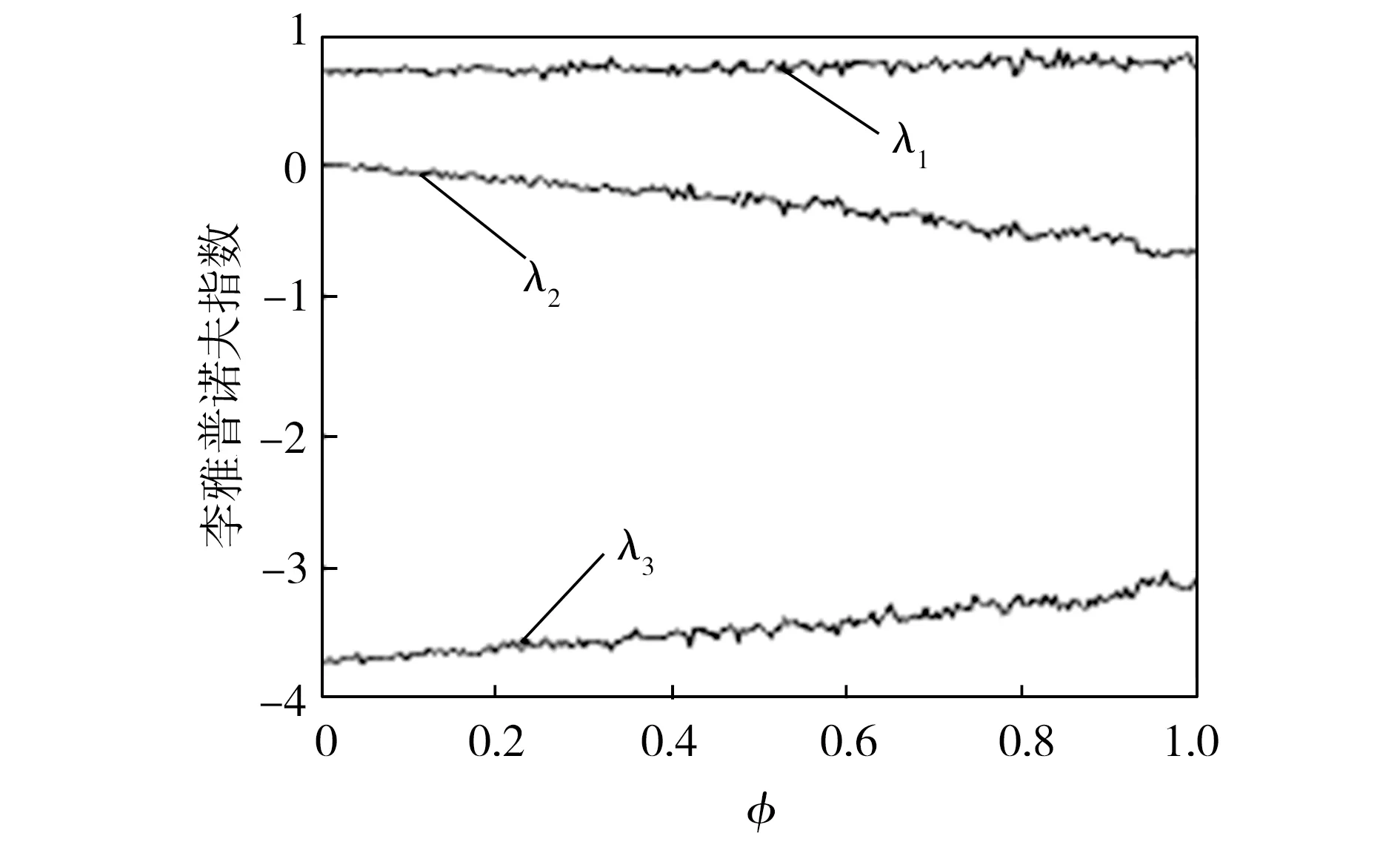
图7 参数变化时的李雅普诺夫指数谱

1.8 切换系统的庞加莱截面和功率谱

为了分析切换系统的动力学特性，利用Matlab软件绘制其功率谱和庞加莱截面图。

图8(a)为切换混沌系统关于变量y的功率谱，图8(b)～图8(d)分别为xy平面关于z=-3、yz平面关于x=0、xz平面关于y=1的庞加莱截面图。

(a)功率谱 (b)庞加莱截面(z=-3)

(c)庞加莱截面(x=0) (d)庞加莱截面(y=1)

图8 功率谱及庞加莱截面图

Fig.8 Power spectrum and Poincaré sections

从图8可以看出，系统的功率谱是连续谱，没有明显的波峰，而庞加莱截面图并非一条封闭的曲线，吸引子的叶片明显可见，进一步表明该切换系统是混沌系统。

2 切换混沌系统的电路设计

通过设计模拟电路来判断本文提出的切换混沌系统能否实现，并对上述理论分析和仿真结果进行验证。图9为所设计的系统电路原理图，其中，用脉冲电压源实现切换混沌系统的切换函数功能，两个脉冲电压源的内部值设置相同，如图10所示。

根据电路原理得到混沌电路的实现方程为：

(15)

将式(15)与式(7)对比，可得：

(16)

以式(16)为约束条件，取值如下：

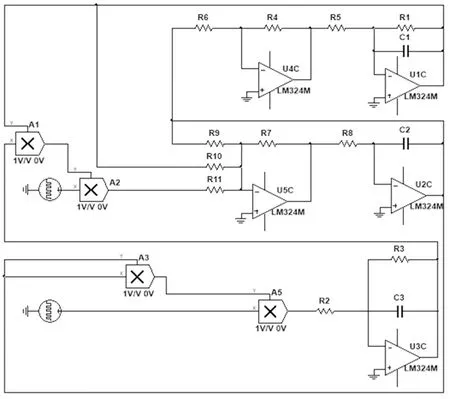
图9 切换混沌系统电路图

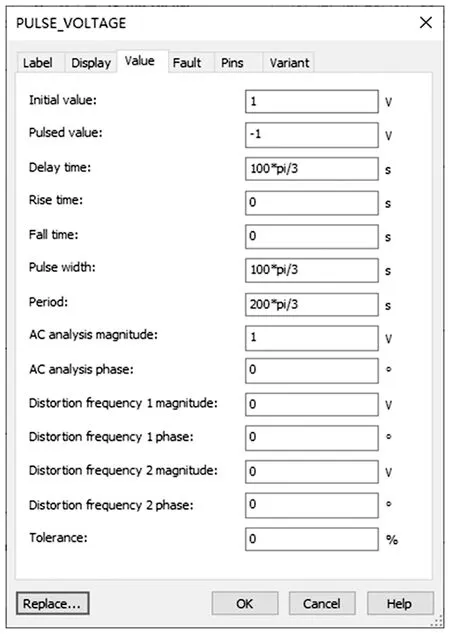
图10 脉冲电压源的参数设置

(17)

从图11～图13可以看出，电路模拟结果与Matlab数值仿真的结果一致，表明本文提出的切换混沌系统能够通过实际电路实现。

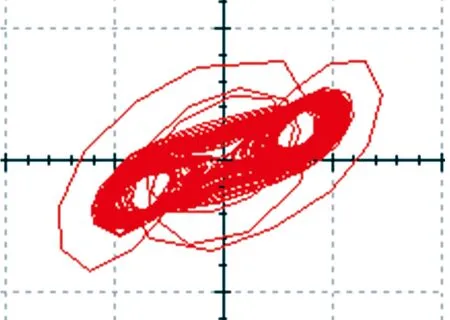
图11 U1-U2相图

图12 U1-U3相图

图13 U2-U3相图

3 结语

本文设计出切换函数，将两个互为反结构的子混沌系统组成一个新的自动切换混沌系统。通过理论计算和Matlab仿真，利用李雅普诺夫指数和维数、分岔图、功率谱、庞加莱截面、平衡点的稳定性等途径对该系统的动力学特性进行分析，并根据混沌系统模型搭建了模拟电路。电路模拟结果与理论计算和Matlab数值仿真结果一致，证实该切换混沌系统可以电路实现。