车联网环境下自动驾驶交通流建模与分析
2019-11-20秦严严余海燕何兆益
秦严严,余海燕,何兆益,冉 斌
(1.重庆交通大学交通运输学院,重庆,400074;2.重庆交通大学经济与管理学院,重庆,400074;3.威斯康星大学麦迪逊分校土木与环境工程系,威斯康星 麦迪逊,53706)
自动驾驶汽车基于车载控制系统与车联网的车车(Vehicle-to-Vehicle, V2V)通信技术实时获取前车行驶状态,有望从微观车辆层面改善交通运营质量。目前实施大规模的自动驾驶实地测试条件还不够成熟,现阶段从交通工程学角度研究自动驾驶微观交通流跟驰模型已成为自动驾驶领域的热点研究问题之一[1]。国内外关于自动驾驶跟驰模型的研究工作大致可以归纳为以下几类:第一类,以传统跟驰模型为基础,通过调节模型参数以及优化设计相关参数来实现自动驾驶交通流跟驰建模[2],这一类建模过程简单且便于应用,但难以从模型结构上区分自动驾驶与手动驾驶的行驶特性;第二类,将自动驾驶跟驰模型结构分为三个部分,第一个部分是通过车联网V2V技术获取前车加速度信息反馈,第二个部分是实际车头间距与期望车头间距的误差项,第三个部分是与前车的速度差项[3],这类自动驾驶跟驰模型从模型结构上直接体现了自动驾驶行驶特性,且模型结构具有物理意义明确的优点,应用较为广泛;第三类,在上述第二类模型结构基础之上,假定车联网技术进一步发展,自动驾驶汽车能够监测多辆前车行驶信息,构建多前车信息反馈结构的跟驰模型[4],这类建模是车联网技术最终发展阶段下的模型结构。
车联网V2V技术的发展需要一个过程,第一个阶段是保证与紧邻前车实现准确可靠的V2V通讯,最后阶段才是车队中多辆车实现V2V互联。本文车联网环境关注的是第一个阶段,即自动驾驶汽车通过V2V技术监测邻近前车加速度状态,这一V2V环境下的自动驾驶跟驰建模工作开展并不够充分,鲜有文献从提升自动驾驶混合交通流稳定性的角度进行自动驾驶跟驰模型的研究,而良好的交通流稳定性是交通运营质量提升的内在机理[5],应用跟驰模型可直接分析交通流稳定性状况,为此,本文在车联网环境下,对原有自动驾驶交通流跟驰模型进行改进,构建新的自动驾驶跟驰模型,并理论推导在不同自动驾驶比例下混合交通流稳定性的解析判别条件,从混合交通流稳定域的角度对比分析模型改进前后混合交通流的稳定性,以期为未来自动驾驶大规模实地测试提供理论参考。
1 跟驰模型的构建
1.1 自动驾驶交通流
国外研究人员针对自动驾驶交通流跟驰建模的研究工作开展较早,其中由VanderWerf等[3]提出的自动驾驶跟驰模型体现了自动驾驶汽车依据车车通讯可获取紧邻前车加速度信息,从而优化自身加速度的行驶特性,模型结构简单且模型参数物理意义明确,一直以来是自动驾驶汽车交通流研究的主流模型,该自动驾驶模型公式[6]为:
kv[vn-1(t)-vn(t)]
(1)
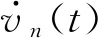
在公式(1)中,自动驾驶汽车的期望车头间距为thvn(t)-d,仅与车速有关,然而在现实的交通场景下,期望车头间距还应当考虑与前车的速度差项,因此,对模型公式(1)进行改进,参考智能驾驶员(Intelligent Driver Model, IDM)模型结构[7],得到新的自动驾驶期望车头间距为:
(2)
式中:s*为自动驾驶汽车期望车头间距,m;T、a、b分别为IDM模型结构中的安全车头时距、最大加速度、舒适减速度,其取值[8]分别为:T=1.5s,a=1 m/s2,b=2 m/s2。
将公式(2)带入公式(1),构建改进后的自动驾驶交通流跟驰模型公式为:
+kv[vn-1(t)-vn(t)]
(3)
对比公式(1)与公式(3)可以发现,改进模型本质上是用IDM模型中的期望车头间距表达式来替换原有模型中期望车头间距项,因而从模型结构上解决了原模型期望车头间距仅与车速有关的缺陷。根据以往对跟驰模型的研究表明,模型结构上的稍小改变仍可较大地改善模型特性,克服原模型的相关缺陷[9],因此,改进后的自动驾驶跟驰模型既保留了原模型结构简单且参数物理意义明确的优点,同时又可反映期望车头间距和当前车速以及与前车速度差之间的相关关系。
1.2 手动驾驶交通流
针对手动驾驶交通流而言,全速度差(Full Velocity Difference, FVD)模型[9]可较好地体现传统驾驶员根据车头间距以及速度差等信息来调节本车行驶车速的驾驶特性,广泛应用于手动驾驶交通流跟驰模型研究,其模型公式[10]为:
(4)
式中:κ与λ为模型系数;V(Δxn(t))表示优化速度函数,即
(5)
式中:v0为自由流速度,m/s;α为系数;s0为最小停车间距,m。
由公式(4)、公式(5)可知,本文FVD模型通过添加车头间距项对原始FVD模型进行了修正,车头间距项可体现驾驶员根据车速调节车头间距的反应过程,能够有效降低模型参数标定误差[11],应用轨迹数据进行模型参数标定的结果[10]为:v0=33.0 m/s,κ=0.629 s-1,λ=4.10 s-1,α=1.26 s-1,s0=2.46 m,标定误差为4.02%,适用于手动驾驶交通流跟驰模型的相关研究。
2 混合交通流稳定性判定
2.1 混合交通流数学表示
由于自动驾驶与手动驾驶构成的混合交通流在车辆空间位置上具有随机性,同时自动驾驶汽车需要通过车联网环境下V2V通信技术获取紧邻前车加速度信息,当一辆自动驾驶汽车的紧邻前车为手动驾驶汽车时,而手动驾驶汽车不具备V2V通信功能,使得该自动驾驶汽车难以实现自动驾驶功能,此时应当由驾驶员接管,即该自动驾驶汽车实现功能退化,变为手动驾驶汽车。因此,在随机的混合交通流中,存在一部分自动驾驶汽车因不具备车联网V2V环境而退化为手动驾驶汽车。这一退化机理与协同自适应巡航控制汽车退化自适应巡航控制汽车的退化机理一致[8],为了避免混淆,用p表示具备自动驾驶功能的汽车比例(简称为自动驾驶比例),该部分包含了的确以自动驾驶功能行驶的自动驾驶汽车比例以及实现功能退化而成为手动驾驶的汽车比例。参考文献[8]的研究结果,在混合交通流中,车辆功能发生退化后的自动驾驶汽车比例(pa)以及手动驾驶汽车比例(pm)分别表示为:
(6)
2.2 混合交通流稳定性推导
定义交通流扰动如下:
(7)
式中:un(t)为交通流速度扰动;ve表示均衡态速度,m/s;yn(t)为交通流车头间距扰动;se表示均衡态车头间距,m。
针对自动驾驶跟驰模型而言,在交通流均衡态下对其进行泰勒展开,同时将公式(7)带入化简得到:
(8)
对公式(8)进行拉普拉斯变换,计算得到自动驾驶交通流扰动传递函数(Fa)为:
(9)
式中:s为拉普拉斯域。
针对手动驾驶跟驰模型而言,同样可应用泰勒公式进行展开并将公式(7)带入化简得到:
(10)
对公式(10)进行拉普拉斯变换,计算得到手动驾驶交通流扰动传递函数(Fm)为:
(11)
令s=jw,将公式(9)与公式(11)由拉普拉斯域转换至频率域,分别得到:
(12)
Fm(jw)=
(13)
式中:j和w分别表示频率域的虚数单位与频率。
根据扰动在混合交通流中的传播特性,应用控制论中的传递函数推导混合交通流稳定性判别条件,即混合交通流传递函数幅频特性的最大幅值应小于1[12],根据这一判别依据,计算本文混合交通流稳定性解析判别条件为:
<1,∀w≥0
(14)
式中:‖·‖表示传递函数最大幅频特性。
当公式(14)的判别条件得到满足时,自动驾驶混合交通流稳定,否则,混合交通流不稳定。从公式(14)中可以看出,混合交通流稳定性与自动驾驶比例(p)以及交通流速度(v)有关。
3 混合交通流稳定性分析
为了分析跟驰模型改进后对自动驾驶混合交通流稳定性的提升效果,应用公式(14)和Matlab软件计算得到不同自动驾驶比例与交通流速度下模型改进前后混合交通流的稳定域,计算结果如图1所示。在图1中,根据模型参数取值的相关研究结果[13],给出了自动驾驶跟驰模型参数的四种取值,分别记为:情况I(ka=1.0,kd=0.2 s-2且kv=3.0 s-1)、情况II(ka=1.0,kd=0.2 s-2且kv=0.58 s-1)、情况III(ka=1.0,kd=0.1 s-2且kv=3.0 s-1)和情况IV(ka=1.0,kd=0.1 s-2且kv=0.58 s-1)。图1中红色区域为混合交通流不稳定区域,蓝色区域表示混合交通流在相应的交通流速度(v)与自动驾驶比例(p)下能够保持稳定状态。从图1中可以看出,相比于原自动驾驶模型,改进后的自动驾驶模型能够进一步缩减混合交通流不稳定区域,有利于从理论层面降低混合交通流全速度范围内稳定时所要求的最低自动驾驶比例p值,从而更好地提升混合交通流稳定性。以情况I为例,对比图1(a)和图1(b)可以看出,原自动驾驶模型只有当自动驾驶比例p达到0.665以上时,混合交通流才能在所有交通流行驶速度下保持稳定,而在改进后的自动驾驶模型下,p只需增大到0.54,即可实现混合交通流在全速度范围内的稳定状态,且自动驾驶汽车最低比例p降低12.5%。此外,图1(a)中10.4 m/s和12.1 m/s表示保证混合交通流全速度范围内稳定时最低p值对应的速度临界值,图1(b)中11.0 m/s和12.4 m/s的含义与其类似。
同样,情况II、情况III以及情况IV的对比结果与情况I类似,均表明改进后的自动驾驶模型相比于原模型而言,更有利于提升混合交通流稳定性,有利于从理论层面降低混合交通流全速度范围内稳定时所要求的最低自动驾驶比例p值,其中情况II、情况III、情况IV下最低自动驾驶比例p值分别降低8.0%、13.5%与7.0%。
根据模型改进前后的混合交通流稳定性分析结果可知,改进后的自动驾驶交通流跟驰模型相比原模型而言,虽然在模型结构上的改变较小,但其混合交通流稳定区域明显扩大,由此可见,模型改进后混合交通流的稳定性得到较大提升。
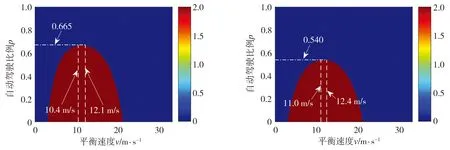
(a) 情况I,改进前 (b) 情况I,改进后
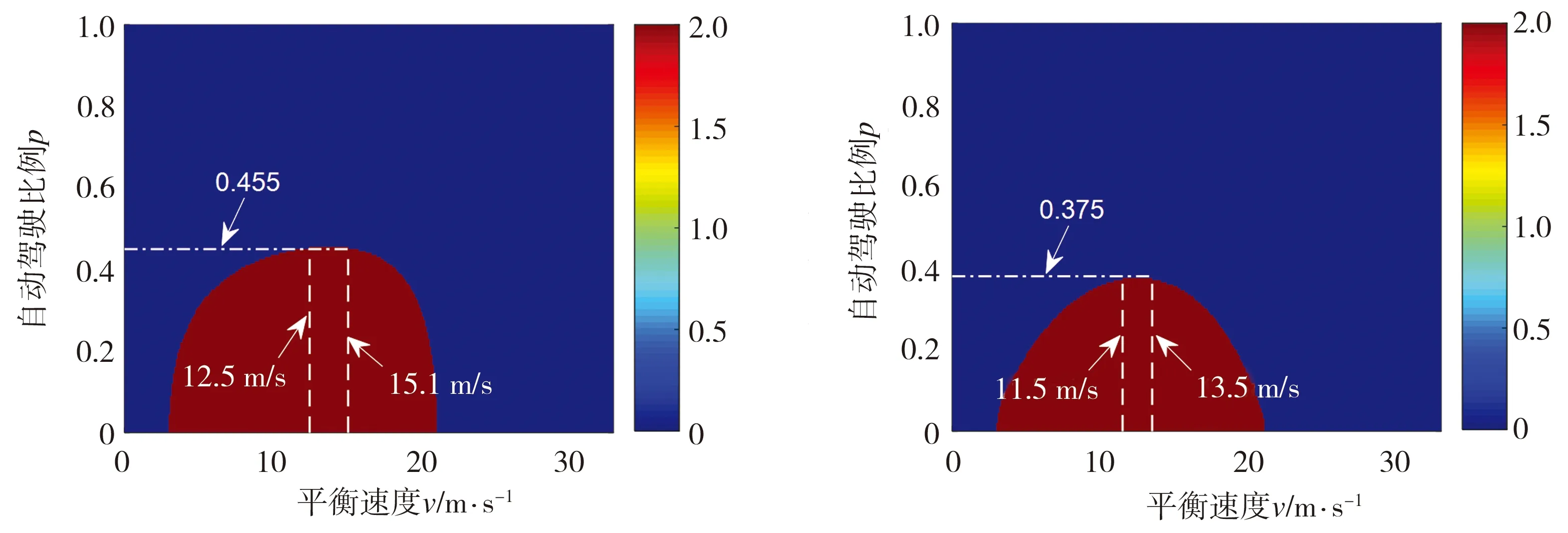
(c) 情况II,改进前 (d) 情况II,改进后
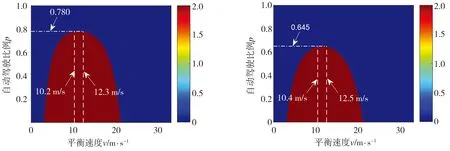
(e) 情况III,改进前 (f) 情况III,改进后
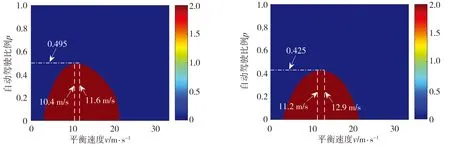
(g) 情况IV,改进前 (h) 情况IV,改进后
图1 自动驾驶跟驰模型改进前后混合交通流稳定区域对比图
Fig.1 Comparison of stability region of mixed traffic flow between original car-following modeland improved car-following model of automated driving
4 结语
针对原有自动驾驶交通流跟驰模型的不足,构建改进后的自动驾驶跟驰模型,与原自动驾驶模型相比,改进后的自动驾驶模型可有效缩小混合交通流不稳定区域,降低混合交通流在全速度范围内稳定时所需的最低自动驾驶比例,更有利于在不同自动驾驶比例下混合交通流稳定性的提升。
