基于人工智能的单坡式防波堤越浪量评估方法研究与应用
2019-11-19刘诗学王收军陈松贵栾英妮
刘诗学,王收军,陈松贵,栾英妮,刘 路,彭 程
(1.天津理工大学 天津市先进机电系统设计与智能控制重点实验室,天津 300384;2.交通运输部天津水运工程科学研究所 港口水工建筑技术国家工程实验室 工程泥沙交通行业重点实验室,天津 300456)
防波堤作为沿海地区重要的工程设施,可以有效的阻挡海浪潮汐的袭击危害。越浪量是防波堤设计的重要指标,同时也是造成防波堤破坏的重要因素[1]。因此,如果可以在设计防波堤过程中合理的估算越浪量,就能方便的兼顾工程安全性和经济性。
传统的越浪量评估方法主要通过大量的物理模型试验,总结出相应的评估公式。例如我国《港口与航道水文规范》[2]中采用的公式是基于王红等人[3-4]的研究成果。同时,大连理工大学的俞聿修等人[5-6]针对不规则波在无胸墙斜坡堤和直立堤上的越浪情况,提出了相应的越浪量计算公式。英国海岸工程设计手册中采用了Owen等人[7-9]的研究成果,其公式考虑了单坡式和复合式斜坡堤两种不同情况。Van der Meer等人[10-13]对斜坡堤越浪进行了系统的实验,他提出的越浪爬高公式和平均越浪量公式被欧洲许多国家采用。日本学者合田良实[14]对不规则波越浪进行了一系列试验研究,其所著《港工建筑物的防浪设计》中的越浪量公式被日本设计人员所使用。美国《海岸工程手册》中的越浪量公式采纳了Ward等人[15]的试验研究成果。俞聿修[16]对多种计算平均越浪量的方法进行了分析比较,并针对不同情况提出各种计算方法的适用性,但由于公式考虑的参数有限,对同一断面结构型式,不同计算公式的计算结果差别较大。
以神经网络为代表的人工智能发展为越浪量的评估提供了新的解决途径。人工智能评估方法具有参数适应性强、评估快速、通过自学习不断完善的特点。欧洲CLASH项目很早便开展了越浪量数据库的建立,目前已经建立了基于人工智能的评估方法。而我国由于缺少统筹,还未开展相关数据库的建立和人工智能越浪量评估方法的研究。本文将根据CLASH数据库以及收集到的越浪量试验数据,建立基于人工智能的单坡式防波堤越浪量评估方法,并利用交通运输部天津水运工程科学研究院的实验结果进行验证分析。文章主要有如下几部分:首先,第一部分介绍了数据的来源和处理方法;第二部分对人工智能算法进行了介绍,并对相关参数的选择进行了分析;第三部分给出了人工智能算法的评估结果,并对该方法的有效性进行了讨论;最后,对研究结果进行了总结和展望。
1 数据来源与预处理
1.1 数据来源与介绍
2002年1月~2004年10月,欧盟启动了一项名为“CLASH”的项目计划。该项目收集了大量的国内外越浪量实验数据,包含了大多数常见的防波堤结构,共计17 942条实验记录。每条实验记录包含40个参数,其中普通变量有3个,波要素参数14个,描述防波堤结构参数23个,图示化说明如下图1所示。
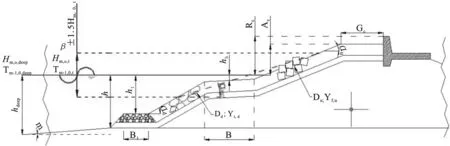
图1 CLASH项目实验参数图示Fig.1 The diagram of CLASH project experimental parameters
本文挑选出单坡式防坡堤结构实验数据作为算法模型的训练集。在这些数据的基础上,研究单坡式防波堤越浪量的模拟和预测。
1.2 数据预处理
1.2.1 数据清洗
数据清洗是指将重复多余的数据筛选清除,将缺失的数据补充完整,将错误的数据纠正或者删除,最后整理成为我们可以进一步加工、使用的数据。按照如下条件删除错误和缺失的试验数据。
(1)删除数据行标签为Non-core data; not used for the ANN的数据行。
(2)删除越浪量Q<10-6m3/s/m的数据行。
(3)删除缺失参数数据的数据行。
(4)删除RF=4或者CF=4的数据行。
其中,RF代表实验的可信度,其取值范围从1~4,RF=1代表实验结果可信度很高,RF=4代表实验结果可信度很低,即RF值越高代表实验的可信度越低;CF代表实验断面的复杂度,其取值范围同样从1~4,CF=1代表实验模型简单,CF=4代表实验模型复杂,即CF值越高代表实验模型越复杂。
1.2.2 数据无量纲化处理
为了消除模型比尺的影响和数据之间的量纲,同时也便于对神经网络进行训练,需要进一步对数据进行无量纲化处理。针对每条实验记录,本文统一把堤前有效波高放缩到Hmo,toe=1 m,并记其放缩比例为λ。根据弗洛伊德定理。
(2)所有与长度相关的参数均乘以λ。
(3)所有与角度和地貌相关的参数均保持不变。

(1)
2 人工智能方法
2.1 BP神经网络模型
BP神经网络是一种多层前馈网络,采用误差逆向传播算法训练。它的学习规则为梯度下降法,即通过反向传播来不断调整网络的权值和阈值,从而使网络的误差平方和最小。BP神经网络模型结构包括输入层、隐含层和输出层。BP算法(反向传播算法)的学习过程,由信息的正向传播和误差的反向传播两个过程组成。构建一个BP神经网络首先需要确定网络的层数和每层的神经元数量。之后,还需要根据训练样本集来确定各层之间的权值系数。

图2 单坡式斜坡堤参数图示Fig.2 Parameters of straight slopes
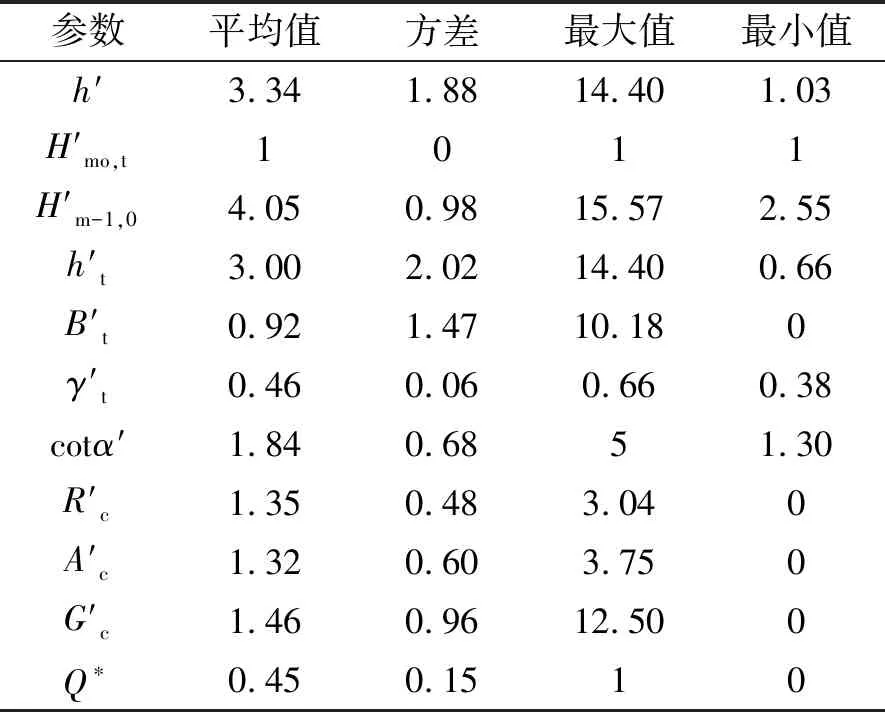
表1 训练集输入参数数据分布特征Tab.1 Distribution characteristics of input parameter data of training set
2.2 建立越浪量神经网络
2.2.1 输入层
根据单坡式防坡堤结构特点,选取10个参数作为网络的输入参数,包括波要素、防波堤结构参数等。如图2所示,分别为堤前有效波高Hmo,t、平均周期Tm-1,0、堤前水深h、堤脚浸没水深ht、堤脚宽度Bt、坡度正切值cotα、护面块体粗糙度γf、挡浪墙顶与静水位之间的高度差Rc、堤顶与静水位之间的高度差Ac、肩台宽度Gc。将实验数据预处理后,各个参数的统计分布特征如表1所示。

图3 隐含层节点数对网络性能的影响Fig.3 Influence of nodal number of hidden layers on network performance
2.2.2 隐含层
隐含层节点数量对于神经网络性能有着较大的影响。本文利用逐步试验法来确定隐含层节点数。即将隐含层节点数从某一初始值逐渐增加,比较每次网络的预测性能,最终选择性能最好的对应节点数作为隐含层神经元节点数。比较结果如图3所示,随着隐含层节点数的逐步增加,网络的性能指标均方误差MSE逐渐减小。但是当节点数从16个再继续增加的时候,MSE值反而增大,这是因为节点数的增加会增加模型的复杂度从而引起过拟合,因此选择隐含层节点数为16个。
激活函数选取tanh函数,它是一种非线性函数,可以将数据变换到[-1,1]之间。即
(2)
2.2.3 输出层
网络输出为1个参数,即越浪量的数值。传递函数选择线性函数pure()函数。即
f(x)=pure(x)=x
(3)
2.2.4 神经网络结构
将神经网络的结构设置好,损失函数为均方误差MSE,即
(4)
上式中,QMi为实验记录中第i个数据的实验值,而QNNi为神经网络给出的预测值。训练函数选为trainlm(),即采用levenberg marquardt算法。
2.3 集成学习
2.3.1 bootstrap重采样
bootstrap重采样是指从一个原始样本中进行有放回的重复采样,采样次数与原始样本的数量相同。原始数据集有N条实验记录,采样次数即为N次,每条实验记录被抽到的概率为1/N。在N次的抽取中,某条实验记录始终没有被抽中的概率为(1-1/N)N,当N趋于无穷大时,该式的值等于1/e,约为0.37。因此,当样本数据很大时,大约有63%的样本数据被选择过,可作为训练集。大约有37%的样本数据从来未被选择过,可作为验证集。
2.3.2 集成学习模型

图4 集成学习模型图示Fig.4 Sketch of integrated learning model
集成学习,是指通过将多个单个学习器集成或组合在一起,使它们共同完成学习任务。该方法基于这样一种思想:对于一个复杂任务来说,将多个专家的判断进行适当的综合所得出的判断,要比其中任何一个专家单独的判断好。它的一般结构是:先产生一组个体学习器,再用某种策略将它们结合起来。
按照集成学习的一般结构,首先产生500组神经网络预测模型,之后采用平均法的组合策略,将它们组合起来综合预测。这样相较于单个模型通常能够获得更好的预测结果。用于越浪量预测的集成学习结合策略示意图如图4所示。
具体的集成学习算法流程如下:
Step1:确定基学习器的个数L=500。
Step2:在训练数据集中,根据bootstrap重采样方法有放回抽样N次(N为训练数据集实验记录总数)。
Step3:重复Step2,一共重复L次,得到L个训练集。(L个训练集之间是相互独立的)。
Step4:基于L个训练集,训练产生L个越浪量神经网络预测模型,每一个模型都会预测出一个Qi值。
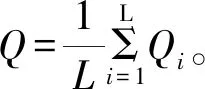
3 结果分析
为了评估人工智能越浪量预测模型的性能,我们将实验数据输入网络中,得到网络的预测值。通过比较预测值和实验值来分析网络的预测性能。同时我们采用评价指标Pearson相关系数R来定量的评价网络的预测性能和精度。相关系数R越接近于1或-1,相关度越强,相关系数越接近于0,相关度越弱。该评价指标的定义如下
(5)
3.1 训练集数据预测
将训练集数据输入到网络中,预测越浪量的值,并将得到的预测值和实验值进行比较,如图5所示。图中中间的斜线为45度理想线,理想线两侧的斜线之间是5倍误差区间带。由于防波堤越浪现象非常复杂,与波要素、防波堤结构形式等诸多因素有关。因此,准确的预测越浪量的值很困难。各家的越浪量计算公式一般控制在10倍误差,即一个量级以内。另外,即使在实验室中对越浪量进行重复测试,通常也会产生5倍的误差。预测结果表明,对于单坡式斜坡堤,该网络预测的越浪量与实验结果具有较好的相关性,相关系数R=0.86,极少出现大的预测偏差,预测结果很可靠。


图5 训练集数据预测比较Fig.5 Comparison of prediction and experimental values in the training dataset图6 不同WF值实验数据预测图Fig.6 Different WF value data prediction
令WF=(4-CF),(4-CF)代表实验可靠度和模型复杂度的综合指标,WF值越高,代表数据本身的可靠性越高,WF值越低,代表数据本身的可靠性越低。由图6可以进一步发现,WF的值越高,数据点越集中分布在45度理想线的附近。相反,WF值低的数据因为本身可信度比较低,所以网络预测的结果也会出现一定的偏差。
3.2 网络的泛化能力
为了验证该网络的泛化能力,我们抽取出100条实验记录。这些实验数据并未参与网络的训练过程,但是他们的参数范围仍然落在训练数据集的范围内。由图7可以看到,对于新的实验数据,网络的越浪量预测值与实验值仍然非常接近,均分布在45度理想线附近,且全部落入5倍误差带范围内。预测值与实验值具有很好的相关性,相关系数R=0.96,表明网络具有很好的泛化性能。


图7 测试集数据预测比较Fig.7 Comparison of prediction and experimental values in the testing dataset图8 工程项目数据预测比较Fig.8 Comparison of prediction and experimental values in the project dataset
3.3 实验数据验证
为了进一步验证该此模型在实际项目工程中的预测性能,本文利用交通运输部天津水运工程科学研究所的实际工程项目实验结果进行验证分析。具体工程为印尼公主港3×350 MW电厂项目的海工工程波浪断面物理模型试验、印尼KARANG TARAJE PORT工程防波堤断面波浪物理模型试验、三亚肖旗港游艇码头改扩建工程波浪断面模型试验。结果如下图8所示,通过比较发现,网络预测值与物理模型实验值很接近,均分布在45度理想线附近,且全部落入5倍误差带范围内。预测值与实验值具有很好的相关性,相关系数R=0.88,进一步验证了该网络模型具有较好的预测性能。
4 结论与展望
本文在欧洲CLASH越浪量数据库的基础上,建立了人工智能斜坡堤越浪量评估方法。该方法不仅可以充分考虑影响单坡式斜坡堤越浪量的十个主要因素,而且具有评估快速、通过自学习不断完善的特点。通过将模型预测的越浪量结果与数据库自身的实验记录和交通运输部天津水运工程科学研究所的实验结果进行对比分析,可以发现人工智能的预测结果和实验结果具有很强的相关性。因此,该模型在设计防波堤过程中不仅可以考虑多种设计因素,也能够在估算越浪量中起到很好的辅助作用,对实际工程中防波堤的允许越浪设计具有重要意义。此外,人工智能预测方法的准确性与训练集有很大关系,该方法的适用范围是指将单坡式防波堤的参数提取出来并经过归一化处理后,各个参数值应位于相应的参数区间内。最后,建议我国尽快启动相关越浪量数据的规范工作,建立更加适合我国海岸防护情况的人工智能模型。
