例谈高考数学应试中的知识点、技术点与智慧点
2019-11-19浙江
浙江
余继光
(作者单位:浙江省柯桥中学)
高考数学复习与解题要关注数学知识点、技术点与智慧点,对于一道数学题,要能认清或分解其中的知识点、技术点与智慧点.数学知识点,一般指必备的数学概念、性质、定理和公式等,为数学基础部分——要知道、了解、理解到位;数学技术点,一般指由知识点串联在一起的程序思维、方法或步骤,强调顺序,不能执行混乱,很多方法属于技术,为数学程序性部分——要掌握到位;数学智慧点,一般指在逻辑推理过程中的变形策略(意识),转化策略(意识),技巧性策略和创造性策略等,为数学解题策略性部分——要积累在脑.
一、数学解题时知识点要“知”
“不知”就是漏点,痛点,解题时可能要走弯路,或多走许多路,出错机会就会增加.
1.要知道它的意义
数学命题中涉及的数学知识点要知道它的意义,比如函数“零点”概念,它是函数与x轴交点的横坐标,不是二维几何点的坐标,而是一维代数点的意义.
2.要了解它的作用
数学命题中涉及的数学知识点要了解它的作用,比如函数零点刻画了函数图象上的一个特点,研究它就可以了解与把握函数的总体特征.
3.要理解它的本质
数学命题中涉及的数学知识点要理解它的本质,比如函数零点研究中“函数零点,方程实根,图象交点”揭示其本质,函数零点可以转化为方程的实根求解,还可以转化为研究两个函数图象交点的横坐标.
数学解题时会涉及许多数学知识点,在知道、了解的前提下,才能顺利解题,否则就会遇到障碍.
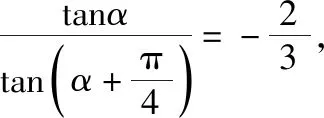
【分析】从题设信息与目标结构来看,需要知道下列知识点:
(1)两角和的正切公式;
(2)两角和的正弦公式;
(3)万能公式;
(4)解分式方程技术;
(5)解一元二次方程技术.
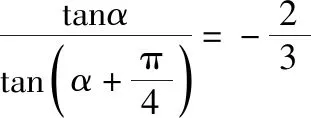
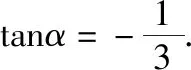
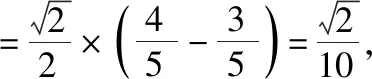
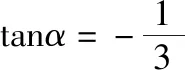
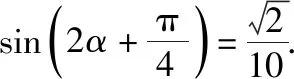
现提出一个真正的学业“减负”观点,多记一个三角公式,可以减少许多不必要的推理,减少许多出错的可能,对于高考数学应试是非常有效的.
二、数学解题的技术点要“会”
数学技术点,一般指由知识点串联在一起的程序思维、方法或步骤,强调顺序,不能执行混乱,很多方法属于技术,为数学解题程序性部分——要“会”,要掌握到位,“不会”就容易错,就会产生痛点,解题就无法进行,或解题过程是错误的,数学解题中所谈到的“数学技术”,不是教学中的“信息技术”手段,是人们还没有重视,还没有认清其作用,在高考数学解题中大量存在“数学技术”缺失的现象.
1.要理解技术的步骤序
数学解题中要涉及大量的运算技术,这些运算本身要涉及运算步骤,简化优先,不懂运算技术,或运算混乱时,出错成为必然.比如,解方程(组)——无理化有理、繁分化简分、分式化整式、繁杂化简洁、移项要变号和增根要验根等.
2.要掌握技术的操作序
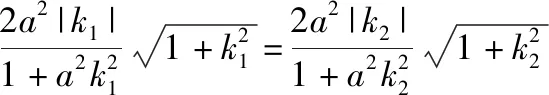
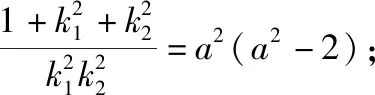
这是2016年浙江高考数学题,许多考生都因为解方程运算技术不过关而丢分.
3.要完善技术的优化序
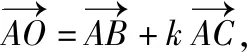
求解上述方程的过程就是优化的,许多考生并不是这样解方程组,一味地代入消元,只会使过程更繁杂.
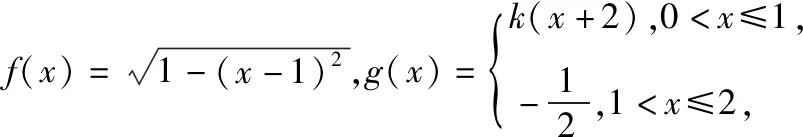
【分析】从题设信息与目标结构来看,需要掌握下列技术点:
(2)会画分段函数图象;
(3)会画周期函数图象;
(4)会画动直线;
(5)会分析两函数图象交点的方法——相切、相交、相离时的情况;
(6)会根据几何条件列方程与解方程.
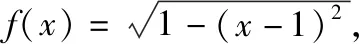
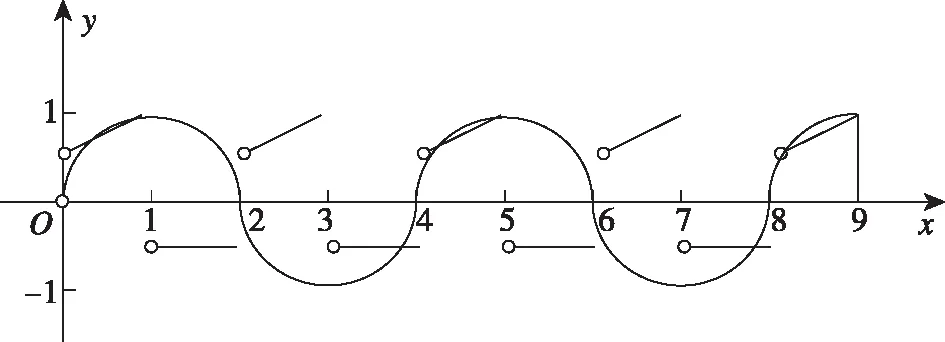
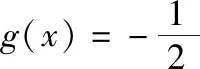
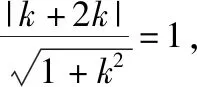
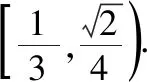
【解读】(1)此题在会技术点的前提下需要知道或理解“奇函数”和“周期函数”的概念;
(3)画图的顺序应该是先画半圆并对称且周期延拓,然后画分段函数的图象并延拓,这个顺序不能乱;
(5)画y=k(x+2),x∈(0,1]的图象,然后周期延拓;
(6)此题画函数图象是“技术细活”,需要建立在对题意理解的基础之上.
三、数学解题时智慧点要“有”
数学智慧点,一般指在逻辑推理过程中的变形智慧(策略),转化策略(意识)和技巧性策略等,为数学解题策略性部分——头脑中要“有”,要积累到位,“没有”就是缺少智慧,就是痛点,解题只能在烦琐步骤下进行.
1.要对智慧点有敏锐意识
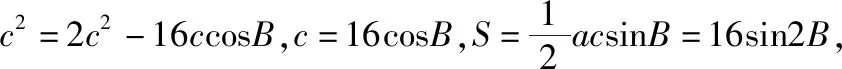
将常数“32”写成“2a2”,为后续的代数推理实施了巧妙的设计.
2.要把智慧点用到该用处
智慧点是策略性“武器”,数学解题时,在该用处能用上相关的策略是智慧点,比如,上面提及的“常数变为变量”的智慧运用.
3.要将智慧点归纳并积累
数学解题智慧点要在平时积累,没有积累在该用时不可能出现,比如,圆锥曲线选填题中,对于“充分挖掘几何图形的几何性质”要平时积累经验与智慧,到用时才会爆发.
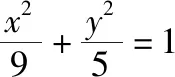
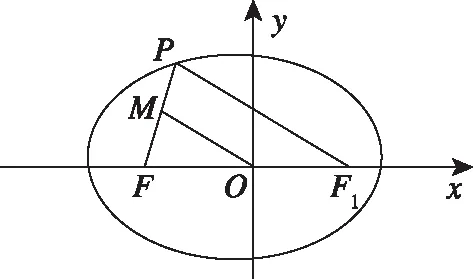
【分析】从题设信息与目标结构来看,需要有下列智慧点:
(1)挖掘出中位线的特征;
(2)挖掘出焦半径;
若不能挖掘出上述几何特征,只能在技术点支撑下进行:
(3)列方程技术;
(4)解方程技术;
(5)求直线斜率的技术.
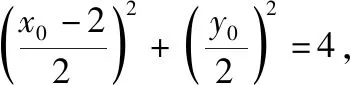
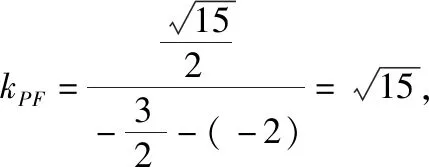
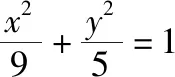
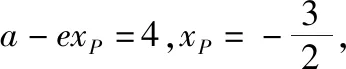
【解读】(1)对于圆锥曲线选填题,当不具有智慧点(挖掘几何图形几何性质的策略)时,一般按照解析法求解解答题的思路进行,即“小题大做”,如解析1;
(2)解析几何是用代数方法解决几何问题的一类题型,离不开列方程解方程,于是就会遇到较多的运算;
(3)几何图形,都具有一些特征,比如中点,中位线性质——数量关系,找到一个几何性质,可能就会减少一些运算;
(4)解析2中发现中点,由中位线性质,找到一个等量关系,建立了关于动点的方程,但没有从根本上解决问题,运算量还比较大;

