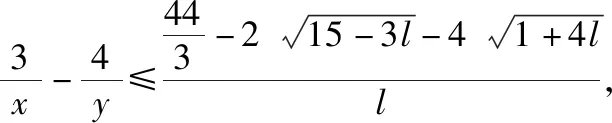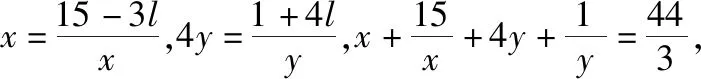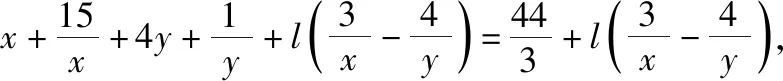从一道竞赛题到一类最值问题的解法研究

陕西

李 歆

(作者单位：陕西省武功县教育局教研室)

在各类数学竞赛和历年高考试题中，最值问题都是常考的重要内容.这类问题往往思考难度大，解题方法活，综合性强，一般学生常感困惑，而解决最值问题最常见的方法之一就是运用均值不等式，但在运用均值不等式之前，常常需要对已知条件或者所求问题进行“变形”处理，这样才能保障解题思路畅通，避免错误的发生.下面通过对一道竞赛题解法的探究，揭示出一类最值问题的通解通法，希望对教师的教学有所帮助.

一、竞赛题呈现

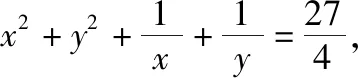
二、解法初探

从结构上看，已知条件是一个较为复杂的等式，左边含有四项，既有整式项，又有分式项，而所求问题是由两个分式项组成，之间连接的是“-”号，比较条件式与所求式的差异，按照化复杂为简单的原则，不妨从条件式入手，先通过变形构造出所求问题式，然后再用均值不等式求解.

【解法1】对已知条件变形，得

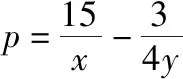
=6，

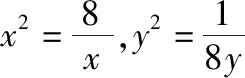
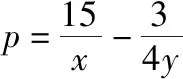
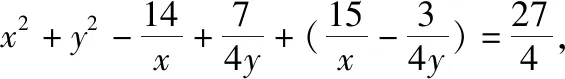
【解法2】对已知条件变形，得

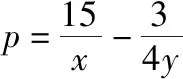
≥16+1-11

=6，

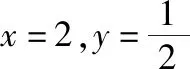
【评注】上述在实施均值不等式之前，解法1用到了拆项法，思路一目了然，解法2用到了添项法，添项时需要借助待定系数法才能准确完成，两种解法的目标都是要消去两个变量x,y，由此说明了拆项法与添项法这两种数学辩证思维方法在解题中的重要作用.

三、变式与拓展

1.改变已知条件与所求问题的顺序

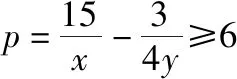
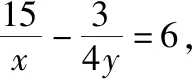
【解法1】由已知条件及均值不等式得

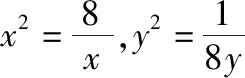
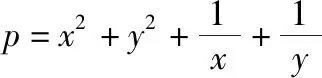
【解法2】由已知条件及基本不等式得

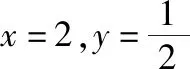
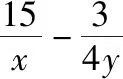
2.将最小值改为最大值

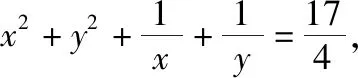
【解法1】对已知条件变形，得

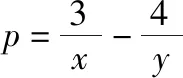
=2，

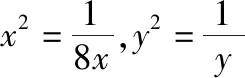
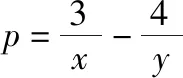
【解法2】对已知条件变形，得

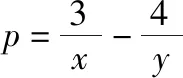
=2，

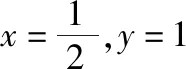
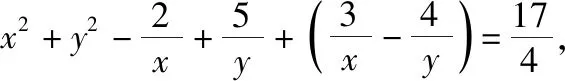
3.引入参数，将问题拓展

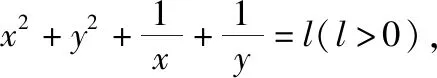
【解析】(1)先求最小值.

设m是满足m>b的待定正实数，对已知条件变形，得

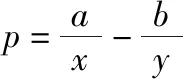
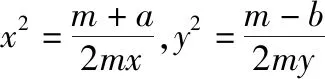
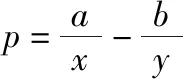
(2)再求最大值.

设n是满足n>a的待定正实数，对已知条件变形，得

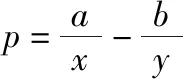
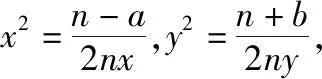
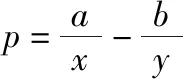
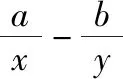
四、解法再探

1.困惑与思考

从上面对竞赛题的变式与拓展中发现，在已知条件中构造所求问题式时，除了在问题式前面添加合理的“+”或者“-”外，还需要配上适当的“系数”，而这个“系数”的确定却不是一件轻松的事，给解题带来了不少的麻烦.那么，还有更好更妙的方法吗？

我们解决数学问题时，通常都是按照从已知条件到所求问题，或者从所求问题到已知条件这两条路径完成的，往往把已知条件和所求问题看成一个问题的两个部分，通过变形与转化，使两个部分和谐统一，最后达到解决问题的目的.如果从数学辩证思维的角度考虑，在解决问题之前，将已知条件和所求问题这两个部分先看成一个整体，即将二者“捆绑”在一起，那么或许能看到解决问题的曙光.

2.竞赛题再解

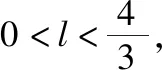
则由均值不等式得

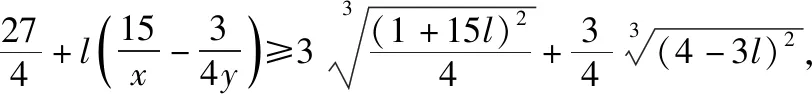
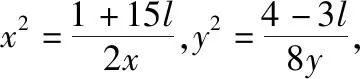
【评注】解法3借助待定系数法，先将所求问题式“捆绑”到已知条件中，不仅入手便利，而且解法快捷.

五、应用举例

通过对一道竞赛题的解法探究，找到了一种解决问题简单实用的新方法：捆绑法，这种方法规律性强，操作方便，用来解决较为复杂的最值问题非常有用.

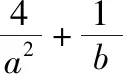
【解析】设l>0，将已知条件变形，得

则由均值不等式得

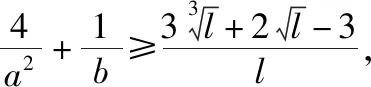
【评注】由于所求问题式的两项的分母出现了非齐次的形式，运用均值不等式解题有一定的困难，但是对已知条件和所求问题式实施“捆绑”之后，却化难为易.

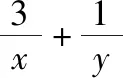
【解析】设l>0，对已知条件变形，得

则由均值不等式得

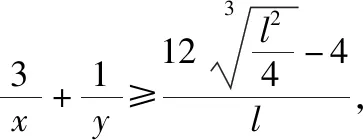
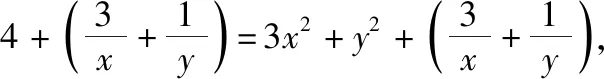
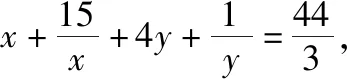
【解析】设0

则由均值不等式得