基于灰色理论与模糊神经网络的导弹性能预测

黄 睿，刘小方，郑 祥

（火箭军工程大学，西安 710025）

0 引言

导弹的打击效果主要取决于自身的性能质量状态，准确掌握导弹的性能质量状态，对于部队作战和管理决策具有重要作用。目前，在导弹部队实弹发射演练中，都是对待发射导弹测试合格后，才实施发射。由于导弹是一个多层次复杂武器系统，数据参数众多，测试耗时耗力，导致在整个演练过程中，技术测试占用了大量时间。但在未来联合作战中，导弹部队面临的必然是大批量、大规模、高效率的作战，如果仍然采用先测试再发射的模式，必然会贻误战机，影响战略决胜。因此，准确预测导弹的性能质量状态是对导弹部队提出的必然要求，也对未来军队联合作战具有重大意义。

灰色预测具有建模所需样本少，计算简单，短期预测精度高等优点，对于小子样，少数据样本，单步预测效果较好［1-2］，因此，可以用灰色理论对导弹性能参数进行预测。神经网络有很强的非线性拟合能力，可映射任意复杂的非线性关系，具有容错能力强、预测速度快、可实现多步预测的优点［3］，同时描述导弹性能质量状态往往需要用模糊语言，所以用模糊神经网络可以将导弹单机子系统的性能质量状态评估值和导弹实弹发射结果信息建立联系，实现对导弹性能质量状态的预测。

鉴于此，本文立足于以往对导弹性能参数的测试数据和日常管理、贮存信息，结合实弹发射结果信息，运用灰色理论、模糊综合评价和模糊神经网络的方法，依次对导弹的性能参数、单机子系统、整弹系统的性能质量状态进行预测，为导弹性能质量状态预测提供一种途径。

1 预测思路

导弹是一个由参数、单机子系统、分系统组成的多层次复杂系统。首先，可以依据以往收集的测试参数信息，运用灰色理论预测导弹的参数数据；其次，根据参数预测结果，结合日常管理、贮存信息，采用模糊综合评价的方法评估导弹单机子系统的性能质量状态；最后，运用模糊神经网络构建模型，建立导弹实弹发射结果信息与其单机子系统性能质量状态之间的联系，从而实现待发射导弹性能质量状态的可靠预测。导弹性能质量状态预测流程如图1 所示：

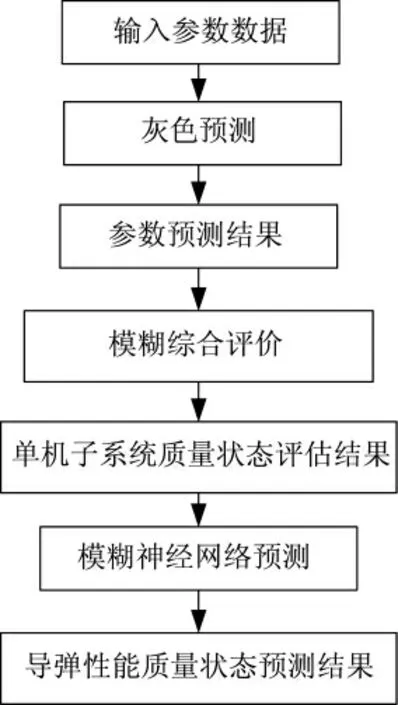
图1 导弹性能质量状态预测流程图

2 基于灰色理论的导弹性能参数预测

以某型导弹弹头的性能参数A 为例，选用GM（1，1）预测模型进行3 年预测（参数A 的测试数据参考表1）。

表1 弹头-参数A 测试数据收集

2.1 预测过程

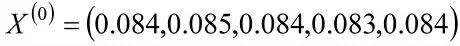
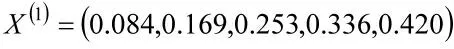
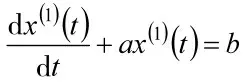
灰色微分方程为：

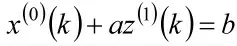
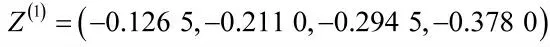
5）白化方程微分的时间响应函数为

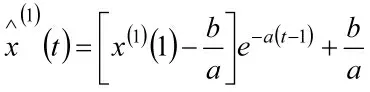
离散化时间响应序列为

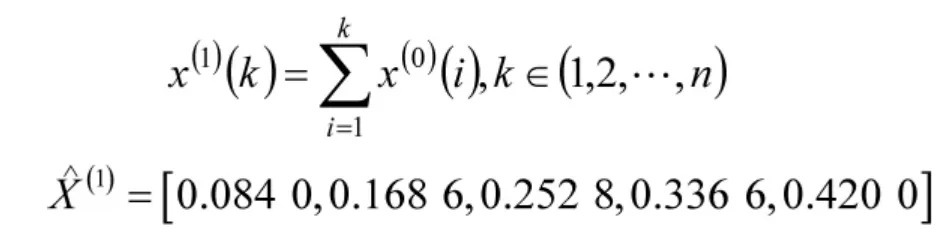
2.2 预测结果

对参数A 的原始数据和预测数据进行对比，如表2 所示。

表2 弹头-参数A 数据预测比较

同理，运用灰色预测可以对该枚导弹的其他性能参数进行预测。

3 基于模糊综合评价法的导弹单机子系统质量状态评估

对导弹单机子系统的性能质量状态评估，不单依靠性能参数指标，还要综合考虑服役履历信息和外观信息等，而这些信息主要来源于日常的管理与贮存。以某型导弹单机子系统弹头为例，建立弹头性能质量状态评价指标体系如图2 所示。运用模糊综合评价法对其性能质量状态进行评估。

图2 单机子系统弹头评价指标体系

3.1 确定评语集

分别用s1，s2，s3，s4表示优秀、良好、一般、不合格4 个等级，则单机子系统弹头性能质量状态空间可表示为S={s1，s2，s3，s4}。

通过专家讨论，并对弹头反复进行比较，最后将不合格（s4），一般（s3），良好（s2）和优秀（s1）对应的主 值 区 间 分 别 划 分 为：［0，0.6），［0.6，0.75），［0.75，0.85），［0.85，1］。

3.2 确定隶属度

本文采用三角模糊函数作为确定隶属度的方法［4］。所构造三角隶属函数为：

不合格（s4）的隶属函数为：

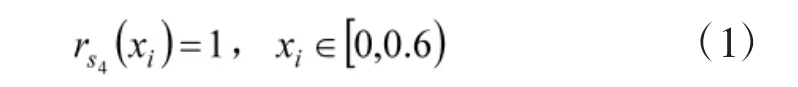
一般（s3）的隶属函数为：

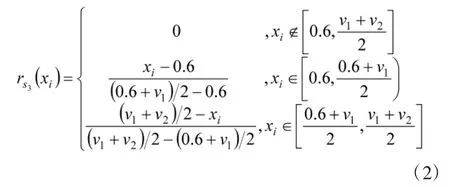
良好（s2）的隶属函数为：

优秀（s1）的隶属函数为：

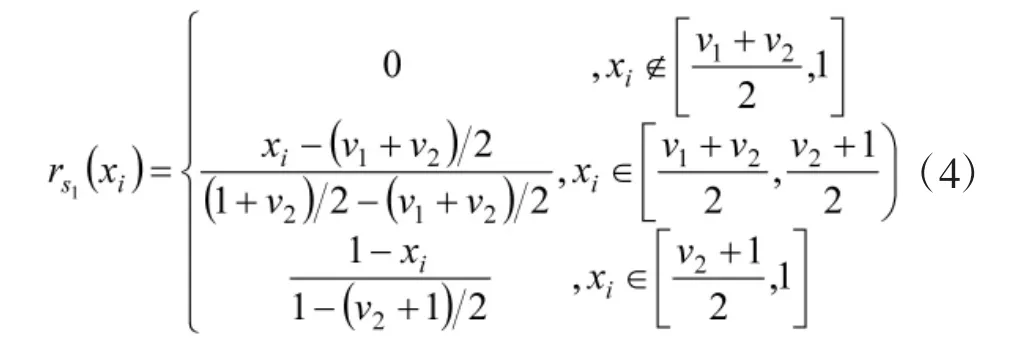
式中：［0，0.6），［0.6，v1），［v1，v2），［v2，1］分别是状态s4，s3，s2，s1的主值区间。

将v1=0.75 和v2=0.85 分别代入上述公式，可进一步得出：

1）不合格（s4）的隶属函数为：

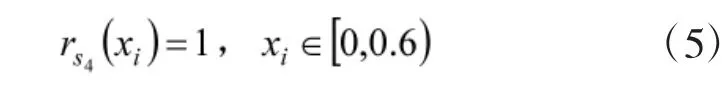
2）一般（s3）的隶属函数为：

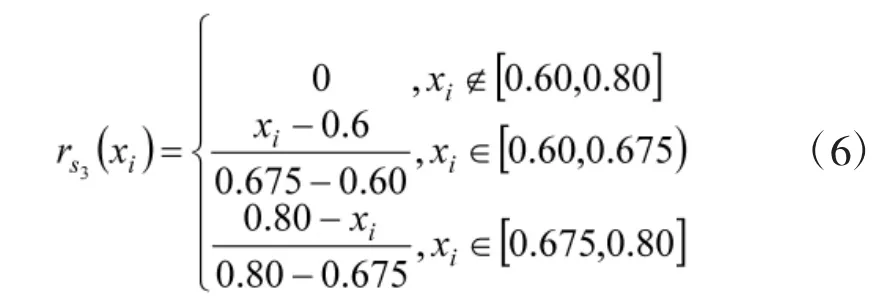
3）良好（s2）的隶属函数为：

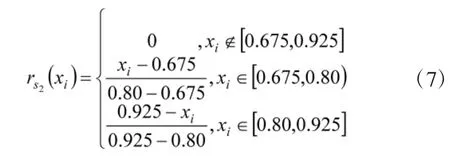
4）优秀（s1）的隶属函数为：

设R 是从U 到V 上的模糊关系，rmn代表第m个因子，对第n 级隶属程度的大小，即第m 个因子对第n 级标准的隶属度。则R 表示为：

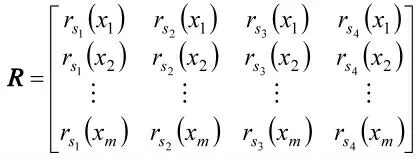
3.3 划分弹头性能质量状态等级

1）弹头的参数指标A、参数指标B 的预测值，服役履历信息、外观信息的评估值及对应的权重，如表3 所示。

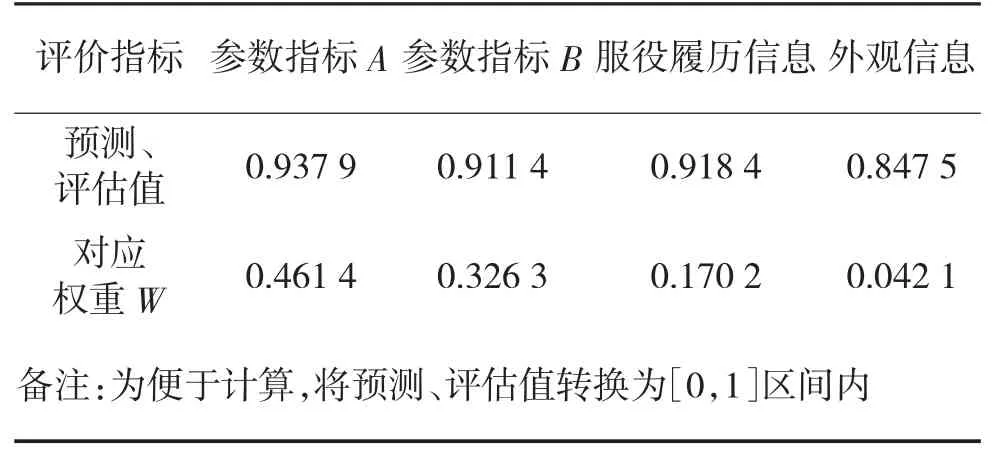
表3 弹头评价指标预测、评估值及权重分配

2）根据三角隶属函数，确定对应指标的隶属度，获取评判矩阵

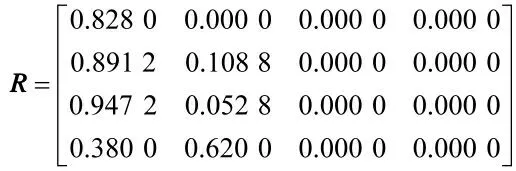
3）获取弹头的评判结果

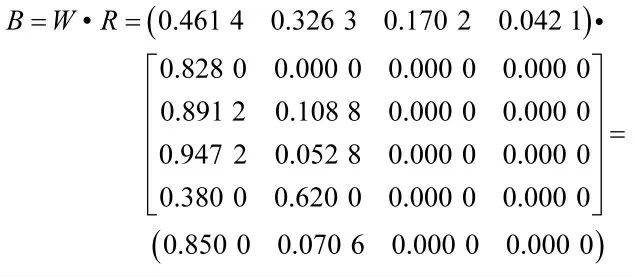
对B 归一化处理得出：

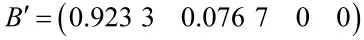
按照最大隶属度原则［5］，确定弹头的性能质量状态为优秀。同理，运用模糊综合评价法可以得到其他单机子系统的质量状态隶属度。

4 基于模糊神经网络的导弹性能质量状态预测

4.1 模糊神经网络预测思路

首先，将导弹实弹打击效果如落点CEP 与整弹系统性能质量状态等级建立一一对应关系，由此根据实弹发射结果将整弹系统的性能质量状态划分为优秀、良好、一般、不合格，将其作为模糊神经网络的输出；然后，以导弹发射前单机子系统性能质量状态评估值作为模糊神经网络的输入，建立由输入层、模糊化层、模糊推理层和输出层构成的4 层模糊神经网络；而后，梳理多枚导弹实弹发射前后的信息，建立一一对应的模糊神经网络的输入、输出，作为样本反复训练所构建的模糊神经网络；最后，对于待发射导弹梳理其单机子系统性能质量状态评估值，作为输入代入训练好的模糊神经网络预测导弹的性能质量状态；在训练过程中，每一次实弹发射的信息均可作为样本对模糊神经网络继续训练，进一步优化网络权重，不断提高模糊神经网络预测准确度。

4.2 模糊神经网络建模

在模糊神经网络模型构建中，采用的是if-then规则：

R：If X1is AK1and X2is Ak2…and Xnis Akn

Then Y1is Bk1and Y2is Bk2…and Ymis Bkm

其中，R 表示规则标志，K 表示规则数目，X=（X1，X2，…Xn）表示一个n 维输入向量，Bkm表示输出向量的模糊集合。

以某型导弹为例构建模糊神经网络模型，该型号导弹有15 个单机子系统，分别以字母I1、I2、…、I15表示。则该模糊神经网络输入节点为15 个，即15个单机子系统性能质量状态评估值。

构建的模糊神经网络输出节点为4 个，分别是［1，0，0，0］、［0，1，0，0］、［0，0，1，0］、［0，0，0，1］，代表“优秀，良好，一般，不合格”。

构建的模糊神经网络隐层数为2，第1 隐含层实际上为模糊综合评定集，每一个节点所对应的实际上是对备选集某一个元素的隶属度，隶属度函数选取三角函数，该隶属度其实第3 节已经由模糊综合评价法给出。第2 隐层的输出实际上是模糊综合指标的选取，其节点数根据如下经验公式获得：

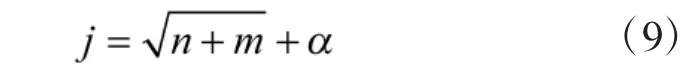
其中，n 是输入节点个数，m 是输出节点个数，α 是1至10 之间的常数。

综合以上分析，设计的某型号导弹性能质量状态预测的模糊神经网络模型如图3 所示。由于从输入层到模糊化层已经在第3 节由模糊综合评价法给出，故在应用该模型时直接输入的是单机子系统性能质量状态隶属度。

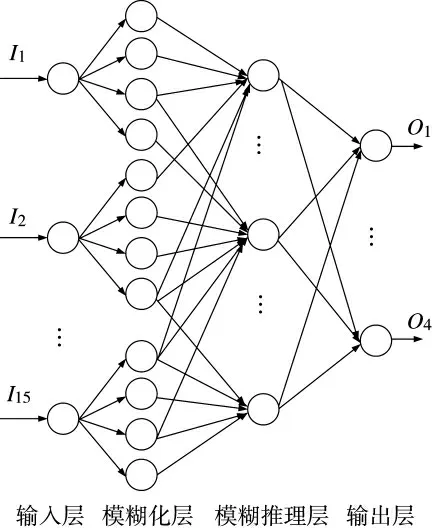
图3 某型号导弹模糊神经网络预测模型

4.3 导弹性能质量状态预测

表4 某部已发射的26 枚导弹性能质量状态隶属度

如表4 所示，以某部已发射的26 枚该型导弹作为训练样本，输入每个单机子系统的性能质量状态隶属度，输出26 枚导弹实弹发射信息对应的性能质量状态等级，对所构建的模糊神经网络进行训练。这里需要说明的是，在收集导弹发射信息时，没有收集到不合格导弹的信息，在此仅根据优秀、良好、一般3 种状态导弹的发射信息，来验证该方法是否可行。

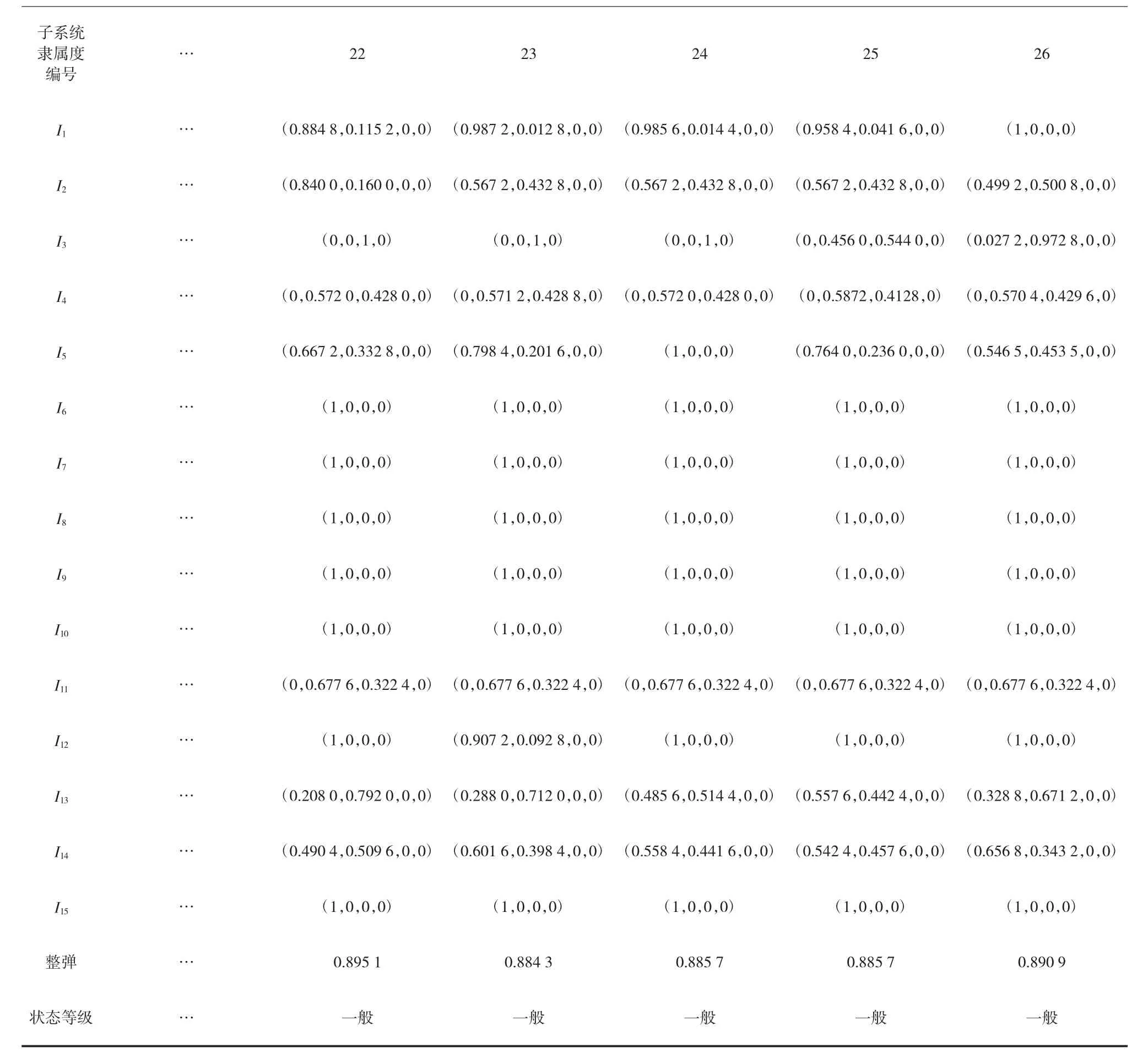
子系统隶属度编号…22 23 24 25 26 I1 … （0.884 8，0.115 2，0，0） （0.987 2，0.012 8，0，0） （0.985 6，0.014 4，0，0） （0.958 4，0.041 6，0，0） （1，0，0，0）I2 … （0.840 0，0.160 0，0，0） （0.567 2，0.432 8，0，0） （0.567 2，0.432 8，0，0） （0.567 2，0.432 8，0，0） （0.499 2，0.500 8，0，0）I3 … （0，0，1，0） （0，0，1，0） （0，0，1，0） （0，0.456 0，0.544 0，0） （0.027 2，0.972 8，0，0）I4 … （0，0.572 0，0.428 0，0） （0，0.571 2，0.428 8，0） （0，0.572 0，0.428 0，0） （0，0.5872，0.4128，0） （0，0.570 4，0.429 6，0）I5 … （0.667 2，0.332 8，0，0） （0.798 4，0.201 6，0，0） （1，0，0，0） （0.764 0，0.236 0，0，0） （0.546 5，0.453 5，0，0）I6 … （1，0，0，0） （1，0，0，0） （1，0，0，0） （1，0，0，0） （1，0，0，0）I7 … （1，0，0，0） （1，0，0，0） （1，0，0，0） （1，0，0，0） （1，0，0，0）I8 … （1，0，0，0） （1，0，0，0） （1，0，0，0） （1，0，0，0） （1，0，0，0）I9 … （1，0，0，0） （1，0，0，0） （1，0，0，0） （1，0，0，0） （1，0，0，0）I10 … （1，0，0，0） （1，0，0，0） （1，0，0，0） （1，0，0，0） （1，0，0，0）I11 … （0，0.677 6，0.322 4，0） （0，0.677 6，0.322 4，0） （0，0.677 6，0.322 4，0） （0，0.677 6，0.322 4，0） （0，0.677 6，0.322 4，0）I12 … （1，0，0，0） （0.907 2，0.092 8，0，0） （1，0，0，0） （1，0，0，0） （1，0，0，0）I13 … （0.208 0，0.792 0，0，0） （0.288 0，0.712 0，0，0） （0.485 6，0.514 4，0，0） （0.557 6，0.442 4，0，0） （0.328 8，0.671 2，0，0）I14 … （0.490 4，0.509 6，0，0） （0.601 6，0.398 4，0，0） （0.558 4，0.441 6，0，0） （0.542 4，0.457 6，0，0） （0.656 8，0.343 2，0，0）I15 … （1，0，0，0） （1，0，0，0） （1，0，0，0） （1，0，0，0） （1，0，0，0）整弹 … 0.895 1 0.884 3 0.885 7 0.885 7 0.890 9状态等级 … 一般 一般 一般 一般 一般

用另外4 枚已发射导弹作为测试样本，将单机子系统的性能质量状态隶属度作为输入代入训练好的模糊神经网络来预测，4 枚导弹的相关信息如下页表5 所示。

该模糊神经网络的训练及预测通过Matlab 软件运行实现。如图4 是模糊神经网络的误差变化曲线，从图中可以看到，当训练至2 731 步时，网络性能达标。表6 是测试样本的预测结果，可以看到4枚导弹的预测结果与实际结果均相符。

5 结论

在未来联合作战中，导弹部队必然面临的是大规模、高效率作战，这就要求导弹部队必须具有迅速发射大批量导弹并且精确打击的能力。但是在目前的实弹发射演练中，通常采取先测试合格再发射的传统办法，虽然能够很好地保证导弹打击效果，但难以满足真正战场的需要。本文立足于以往对导弹性能参数的测试数据和日常的管理、贮存信息，运用灰色理论、模糊综合评价方法，分别对导弹性能参数进行预测、单机子系统性能质量状态进行评估，最后在深入研究实弹发射结果信息的基础上，运用模糊神经网络对整弹性能质量状态进行预测，为导弹性能质量状态预测提供了一种思路。实例表明，该方法能够准确预测导弹的性能质量状态。

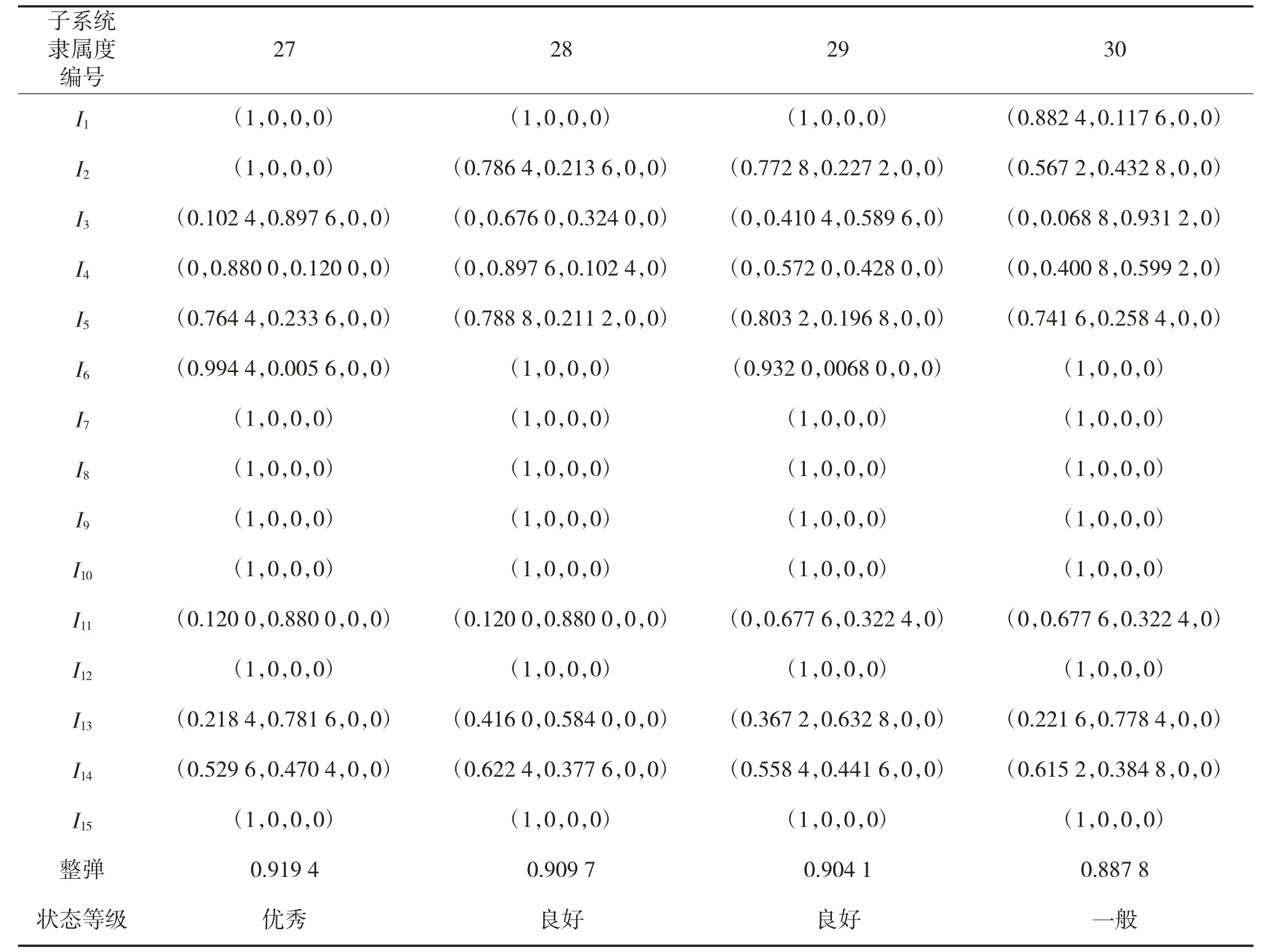
表5 某部已发射的4 枚导弹相关信息

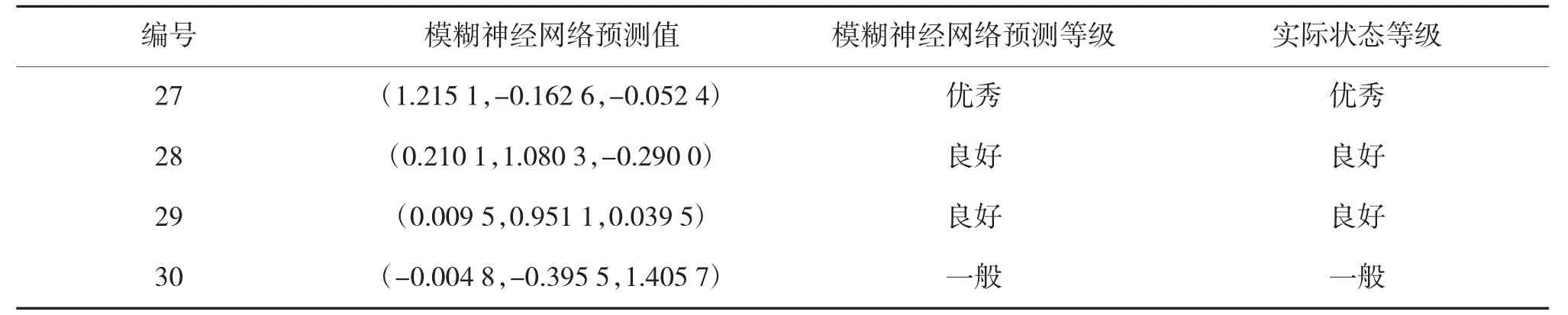
表6 模糊神经网络模型预测结果

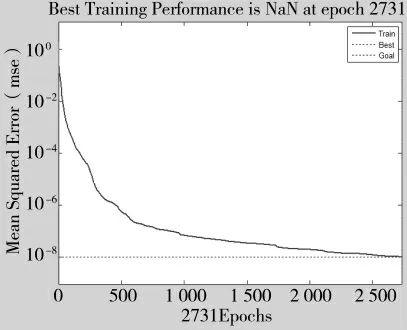
图4 模糊神经网络误差变化曲线