共形阵列方位依赖幅相误差校正辅助阵元法*

侯文林，胡 月，谢吉鹏

（空军通信士官学校，辽宁 大连 116600）

0 引言

共形阵列［1-9］是未来天线发展的主要方向，对信源的高分辨波达方向（direct of arrive，DOA）估计是阵列天线的主要功能之一，阵列误差校正技术是阵列天线DOA 估计技术走向工程实用的前提基础，因此，对共形阵列误差校正的研究具有重要的理论意义和实用价值。

阵列误差校正可归结为幅相误差校正问题［10］。根据幅相误差是否依赖信源方位，将幅相误差分为方位无关的幅相误差和方位依赖的幅相误差。方位依赖的幅相误差是阵列误差校正的难点，其原因是不同的信源方位对应的幅相误差不同，两者相互耦合，若无已知信息参考，很难实现误差校正。在共形阵列中，方位依赖的幅相误差更为严重，原因有两点：一是共形阵列工作环境极为复杂，通常同时存在幅相、互耦和阵元位置等多种误差，需要用方位依赖幅相误差对阵列误差进行综合性描述；二是受共形载体曲率影响，共形阵列中天线单元对入射信号的响应不一致，它与阵列误差相互耦合，故需用方位依赖幅相误差对共形阵列误差模型进行描述。文献［11］提出一种共形阵列天线互耦校正的辅助阵元法，可推广至信源方位和方位依赖幅相误差的联合估计，但该算法需要辅助阵元数大于信源数。文献［12］提出一种面阵阵元位置误差自校正的累积量域辅助阵元法，也可推广至共形阵列方位依赖幅相误差校正，所需辅助阵元数P 与信源数M 的关系为P（P+1）/2>M，虽小于文献［11］中算法，但仍随信源数增加而增加。上述算法都假设信源同频窄带，但在实际应用中这个假设可能不成立，故适用于不同频率的窄带信源、所需辅助阵元更少的共形阵列方位依赖幅相误差校正算法具有重要意义。

针对任意形状共形阵列方位依赖幅相误差校正问题展开，首先利用时域旋转不变子空间（ESPRIT）的思想［13］，得到满足旋转不变性的成对快拍数据，及协方差矩阵和四阶累积量矩阵，进而估计出阵列的流型矩阵和信源频率；然后结合3 个远离共形载体精确校正的辅助阵元和线性方程组求解估计出信源方位和方位依赖幅相误差。

1 共形阵列方位依赖幅相误差模型

受共形载体曲率的影响，共形阵列具有多极化特性，不同天线单元对单位强度入射信号的响应ri（表示第i 个阵元对入射信号的响应）可能不一致。对于任意形状的共形载体，ri为关于天线单元方向图和信源极化参数的函数［14］，都可表示为：

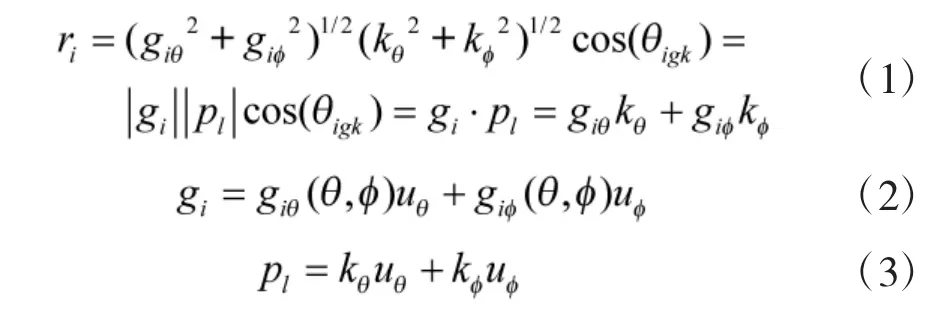
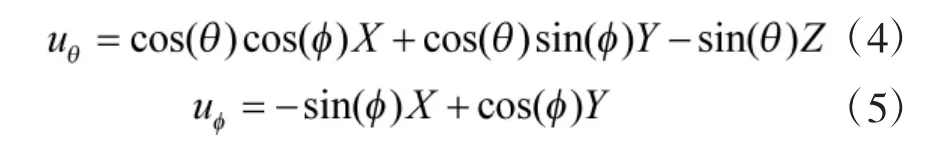
图1 阵元在全局坐标系中对入射信号的响应

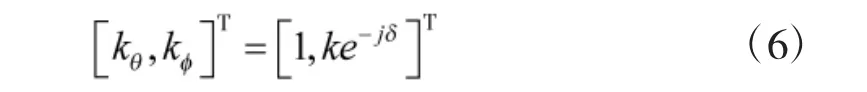
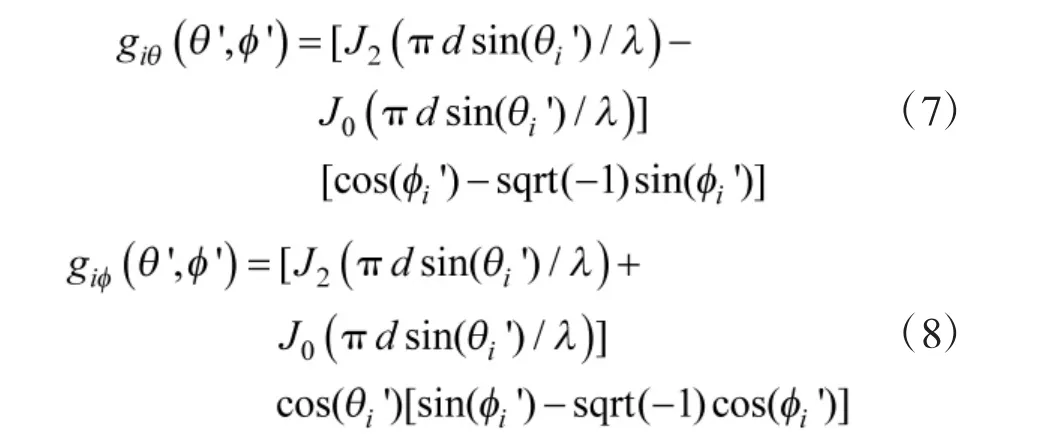
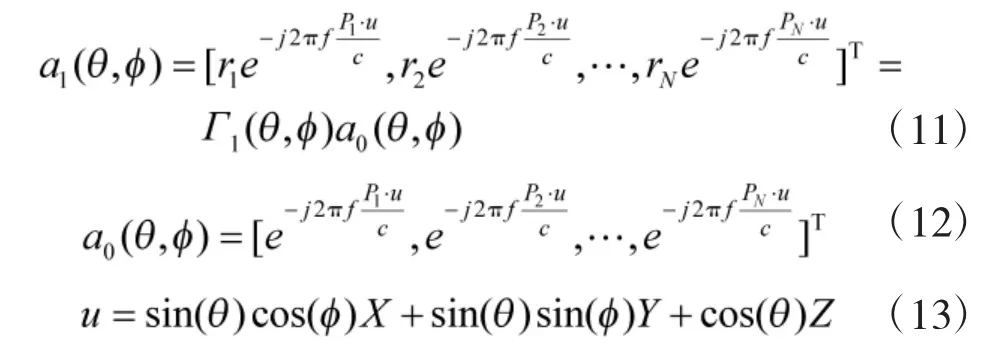
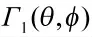
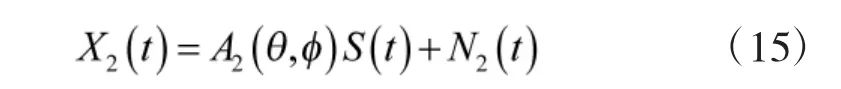
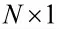
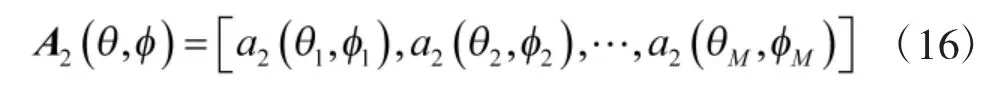
2 柱面共形阵列幅相误差校正

ESPRIT 算法不需要参数搜索，即可实现信源方位的估计，可极大地降低算法运算量。但ESPRIT 算法要求阵列可划分为具有旋转不变性的子阵，若共形阵列中存在方位依赖的幅相误差，很难满足此要求。在此借鉴延时构造旋转矩阵的思路［13］，构造旋转子阵，将ESPRIT 推广至任意载体的共形阵列，再结合3 个精确校正的辅助阵元，估计信源频率、方位和方位依赖幅相误差。

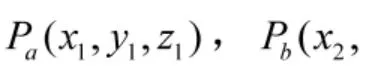
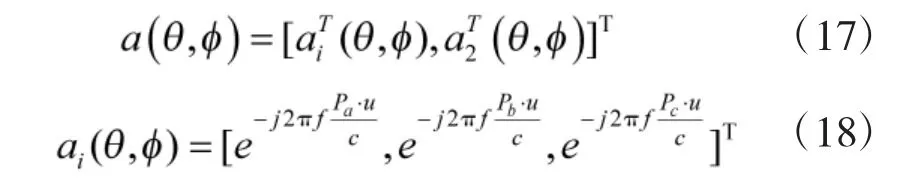
此时整个阵列的接收数据可表示为：

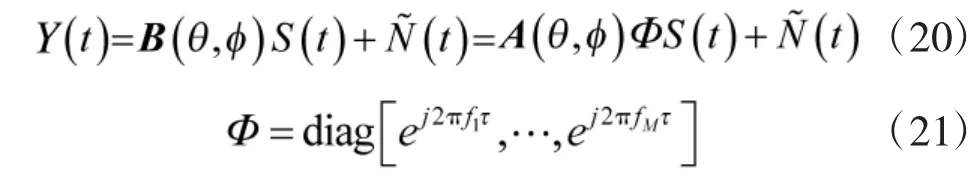
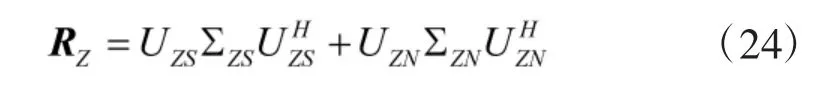
式中，UZS为信号子空间的基，由M 个大特征值对应的特征矢量构成；UZN为噪声子空间的基，由2N+6-M 个小特征值对应的特征矢量构成。取UZS的前N 行记为UZS1，后N 行记为UZS2。可得：

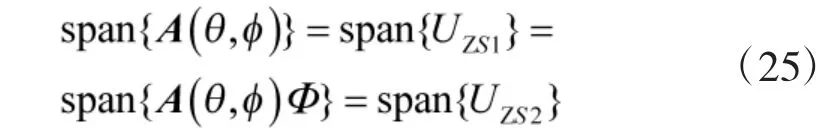
存在唯一的非奇异矩阵T 使得：对应最小二乘ESPRIT 算法，可解得：

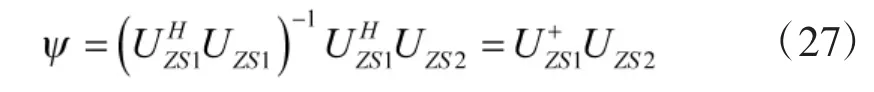
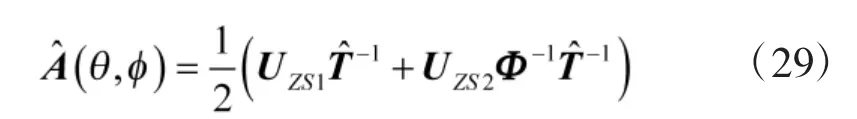
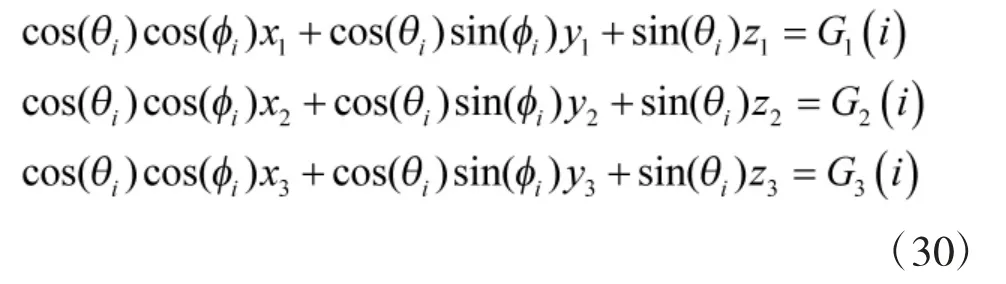
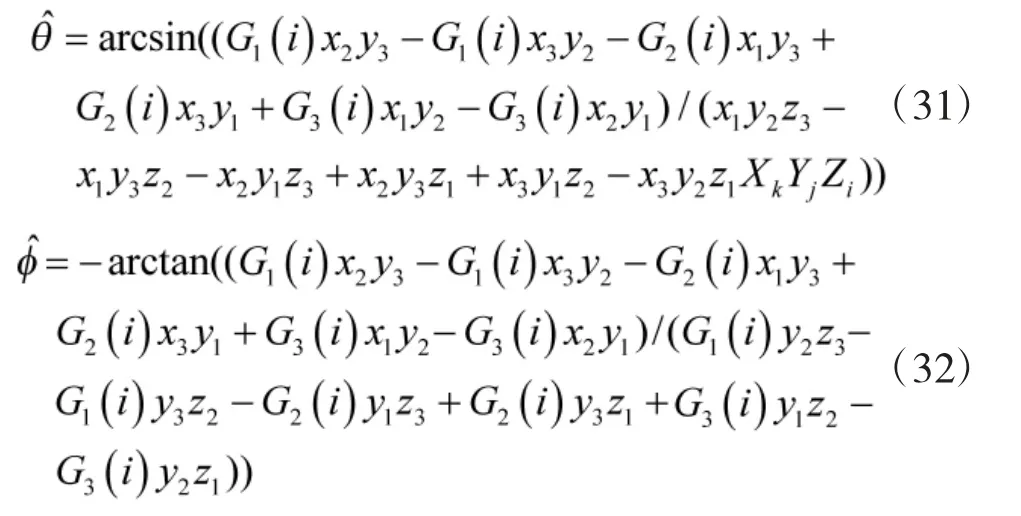
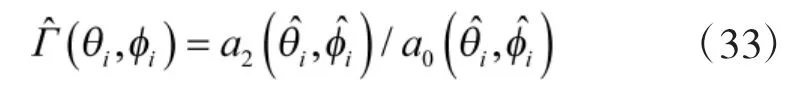
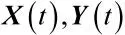
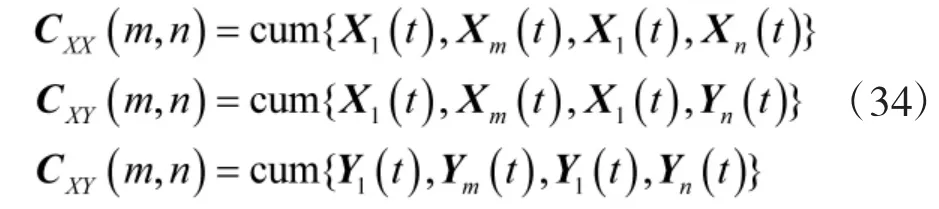
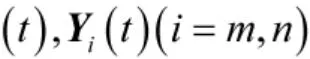
故可构造一新的矩阵CZZ如下：

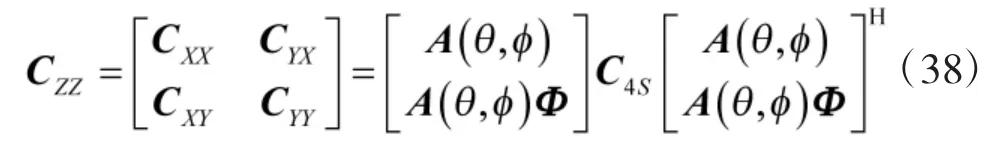
综上所述，共形阵列方位依赖的幅相误差校正算法的流程如下：

2）分别由式（23）和式（38）得到接收数据的协方差矩阵RZ和四阶累积量矩阵CZZ；

3）对协方差矩阵和四阶累积量矩阵特征分解，得到信号子空间对应的特征矢量UZS；

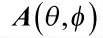
5）由式（31）～式（33）得到信源方位和方位依赖幅相误差的估计值。

3 仿真实验

现对上述所给算法进行Monte-Carlo 仿真实验验证。成功实验的定义为：估计偏差小于2°的试验为成功实验。成功概率的定义为：成功试验次数与试验次数的比值。估计偏差定义为：在成功实验中，估计均值与真值之差的绝对值。估计标准差定义为：在成功实验中，估计值与估计均值之差的均方值开方。在此前提条件下，进行100 次独立仿真实验。

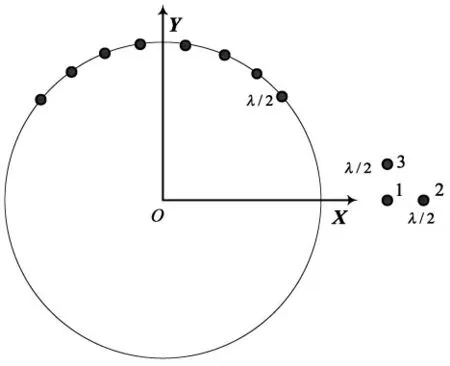
图2 阵列结构示意图

3.1 仿真实验1

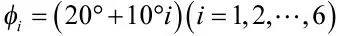
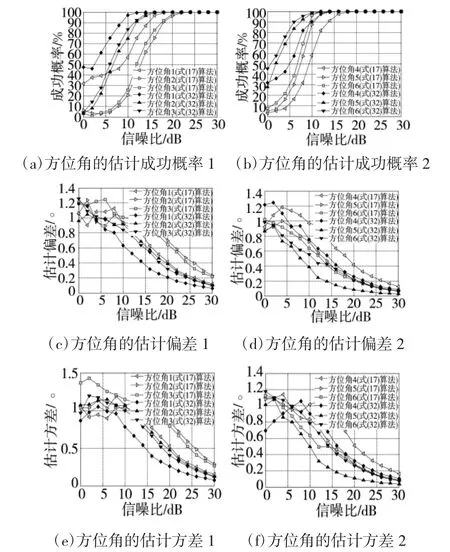
图3 方位角的估计效果曲线

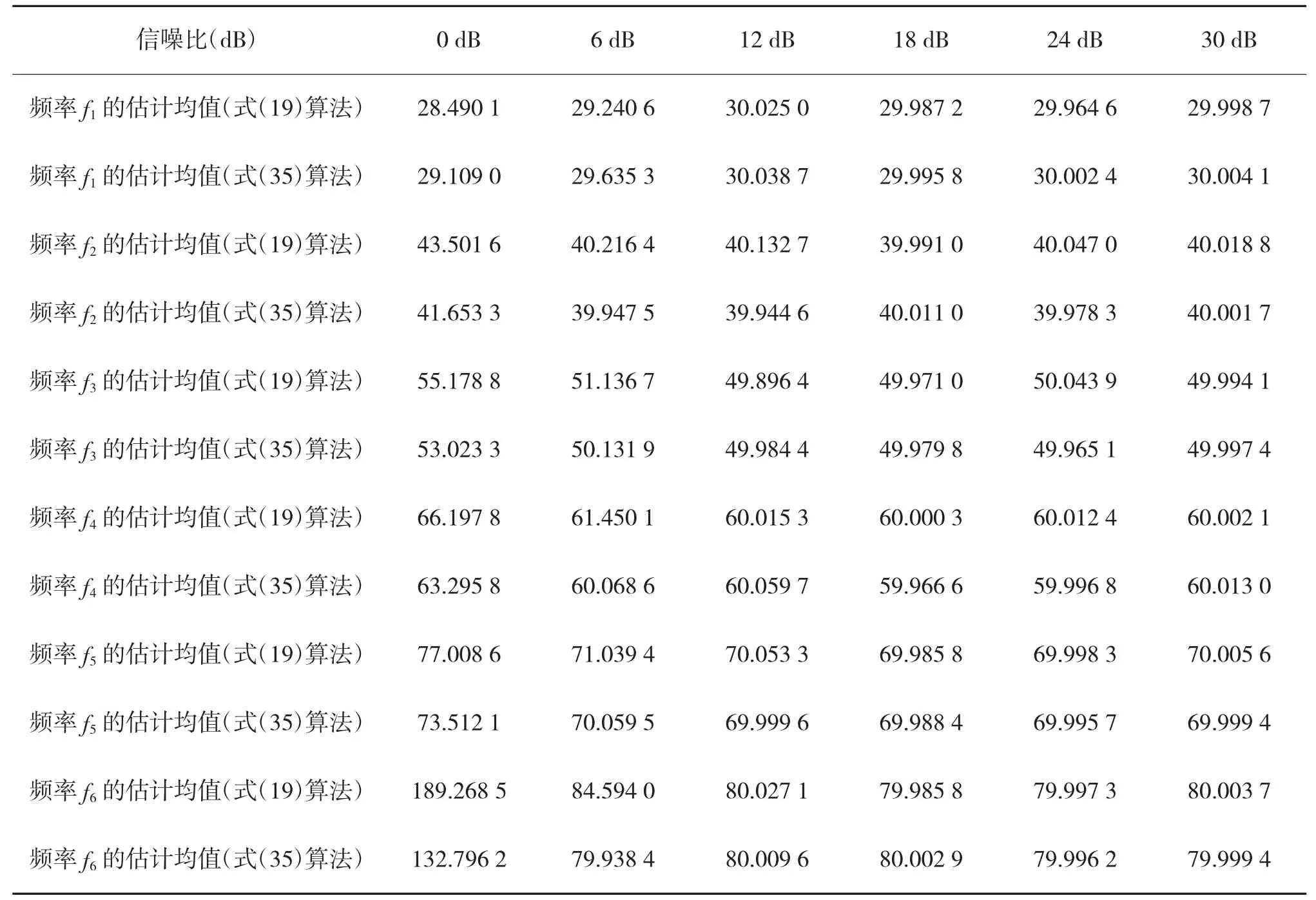
表1 信源频率的估计（真值为f1=30，f2=40，f3=50，f4=60，f5=70，f6=80）

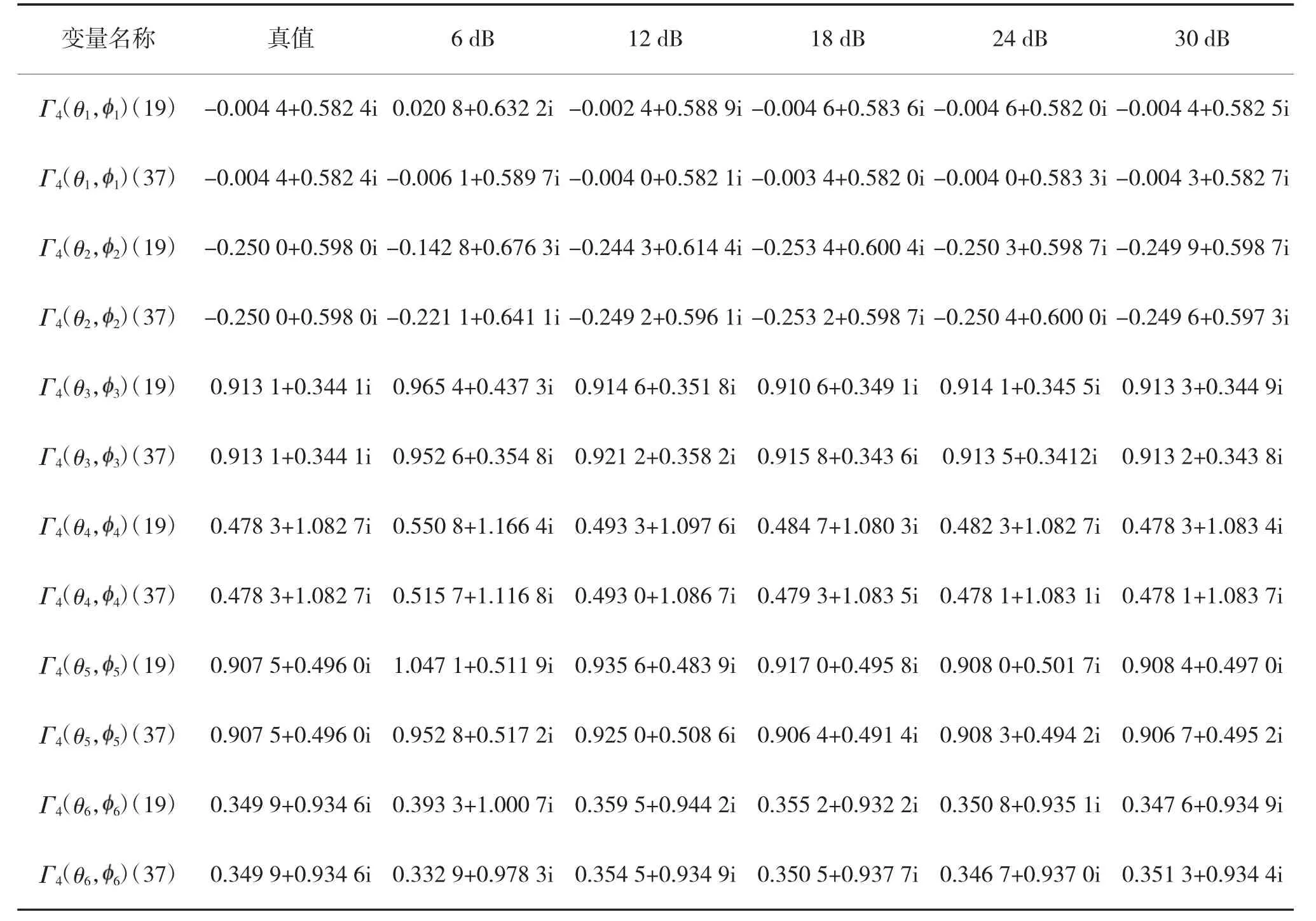
表2 阵元4 方位依赖幅相误差的估计

实验结果表明，随着信噪比的增加，本文所给算法性能也随之变好。在方位角为低角度时（如方位角为30°时），需信噪比大于20 dB，方位角的估计成功概率才可达到100%，如图3（a）所示；在方位角为较高角度时（如方位角为80°时），在信噪比大于12 dB 时，即可使方位角估计成功概率达到100%，如图3（b）所示，这符合信源方位角的估计特性。另外，式（38）算法性能优于以上两者，这是因为高阶累积量可有效抵消噪声的影响。由表1 与表2 可知，当信噪比较低时，信源频率和方位依赖的幅相误差估计效果较差；随着信噪比的增加，估计效果逐渐变好，当信噪比充分大时，参数估计均值达到了很好的效果。

3.2 仿真实验2

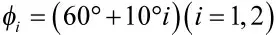
图4 方位角的估计效果曲线

实验结果表明，式（19）算法方位角估计性能与文献［11］算法相当，式（35）方位角估计性能优于文献［11］中算法估计性能，这是四阶累积量可以有效抵消噪声干扰的原因；随着信噪比的增加，两者性能都随之变好，在信噪比大于6 dB，方位角估计成功概率均可达到100%，从而证明了所给算法的有效性。

4 结论

本文通过引入3 个远离共形载体精确校正的辅助阵元，实现了频率不同、信源数任意时的方位依赖幅相误差校正，且适用任意阵型，无需参数搜索和配对。首先通过延时接收信号构造满足旋转不变性的快拍数据、其协方差矩阵和四阶累积量矩阵；然后通过时域ESPRIT 算法估计出信源频率和阵列流型矩阵；再利用3 个远离共形载体精确校正的辅助阵元和线性方程组，求解估计出信源方位和方位依赖幅相误差，最后Monte-Carlo 仿真实验验证了所给算法的有效性。