基于转角和啮合点关系的内啮合齿轮泵排量精确计算

2019-11-18

液压与气动 2019年11期

(太原科技大学机械工程学院，山西太原 030024)

引言

齿轮泵是液压传动系统中常用的液压元件，其中内啮合齿轮泵因齿轮同向旋转，相对滑动速度小，磨损轻微，使用寿命长。同时又具有结构紧凑、高效、低噪音等突出优点[1]得到了广泛应用。但同时对齿轮泵的排量的准确计算也是齿轮泵设计、制造和使用中常见的问题。

何存兴为便于齿轮泵排量在实际工程中计算给出了估算公式，而后李宏伟在此基础上提出另一种近似公式来估算排量[1-2]。杨国来等[3]基于直线共轭内啮合齿轮泵，定义了其啮合角函数并进一步推导出了直线共轭齿廓方程。钱志达等[4]针对不同传动形式的内啮合齿轮泵推导了一系列排量公式。邹旻等[5]针对谐波式齿轮泵进行了排量计算。吕程辉等[6]基于Fluent动网格技术，对内啮合齿轮泵内部流场进行了二维非定常计算，得到了其在不同工况下的流场特性。吴晓明等[7]基于AMESim搭建内啮合齿轮泵的流量动态子模型，分析了泵的流量、压力脉动特性并得出一系列影响脉动的因素。郭善新[8]针对啮合齿轮齿间有无侧隙情况对内啮合齿轮泵排量的精确计算。董亚敏[9]

通过推导齿轮齿厚与压力角关系式，得出内啮合齿轮泵排量在一定程度上随压力减小而增大。李玙璠等[10]基于SimulationX预测了泵的输出特性以及齿间容积内达到的最大和最小压力。目前内啮合齿轮泵排量的计算基本利用经验公式，对研究齿轮泵的流量特性及其影响因素缺乏指导意义，因此对其进行排量精确推导尤为必要。

1 齿轮转角与啮合点关系

如图1所示，根据内啮合齿轮泵的啮合原理及能量守恒定律易得齿轮泵瞬时流量表达式为[1]：

(1)

式中，B—— 齿宽

ω—— 外齿轮轴的角速度

x—— 啮合点到外齿轮中心的距离

y—— 啮合点到内齿轮中心的距离

R1，R2—— 外齿轮和内齿轮节圆半径

Re1，Re2—— 外齿轮和内齿轮齿顶圆半径

图1 简化内啮合齿轮泵工作原理图

公式中x，y随齿轮的转动角度β而变化，且具有一一对应关系，因此求解该关系式有助于得到内啮合齿轮泵瞬时流量和理论排量明确的解析。

由齿廓的渐开线方程[11]：

(2)

式中，rK—— 渐开线上一点K到基圆中心的距离

Rb—— 齿轮的基圆半径

α——K点的压力角

θ——K点的展开角

对外齿廓而言，某瞬时啮合点在K1，外齿轮轴转过角β1后的啮合点为K2，而K2的初始位置为K0点，如图2所示。

图2 外齿轮啮合点和转角关系

易得如下角度关系：

β1=(α′1-α1)+(θ1-θ1)

=tan(α′1)-tan(α1)

(3)

式中，α1,θ1—— 啮合点K1处的压力角和展开角

α′1，θ1—— 啮合点K2处的压力角和展开角

故：

α′1=arctan(tan(α1)+β1)

(4)

则外齿轮转动角度β1后，啮合点K2到外齿轮中心的距离为：

(5)

对内齿廓而言，某瞬时啮合点在K1，外齿轮轴转过角β1，内齿轮同向转过的角度为β2，此时啮合点为K2，且K2转动之前的位置为K0点，如图3所示。

图3 内齿轮转角和啮合点关系

内齿轮转动角度β2后，同理推导易得：啮合点K2到内齿轮中心的距离为：

(6)

式中，α2，α′2分别为内齿廓上啮合点K1和K2处的压力角。

2 排量分析

(7)

内啮合齿轮泵的排量分析即研究主齿轮(外齿轮)转动一圈泵吸入或者排出的油液体积。考虑到齿轮啮合传动的连续性，以及内啮合齿轮泵作为容积式液压泵，其高低压密封的可靠性。一般设计内啮合齿轮副重合度ε大于1。即上一对轮齿还未退出啮合状态的时候，下一对轮齿就已进入啮合。

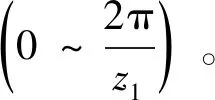
又ωdt=dβ1，则这对轮齿排出的油液体积为：

(8)

故内啮合齿轮泵的排量公式为：

(9)

式中，z1和z2分别是外、内齿轮的齿数。

计算式(9)中的α1和α2，即起始啮合点K1相对于外齿轮和内齿轮的压力角是精确求解排量的关键。

则将上值代入式(4)，得:

(10)

同理，对于内齿轮而言，易得到:

(11)

式中，α″为内啮合齿轮副节圆压力角。

对于变位内啮合齿轮副，其节圆压力角(即啮合角α″)和重合度ε计算如下[11]：

(12)

式中，a，a′分别为齿轮泵变位前、后的中心距。

(13)

式中，αa1，αa2分别表示外齿轮和内齿轮的齿顶圆压力角。

基于上述分析计算易知，内啮合齿轮泵排量本质上是由齿轮副的模数、齿数、齿顶高系数、分度圆压力角、齿宽和变位情况决定。虽然上述方法对齿轮泵排量的计算较为复杂，但能较为全面反映各因素对排量的影响情况，因而本研究所得出的排量计算方法对参数优化以及流量脉动分析都具有指导意义[12]。

3 界面化程序设计

由于本内啮合齿轮泵的排量计算公式推导和计算较为复杂，为方便在实际工程中的应用，基于LabVIEW中公式节点，对排量公式作了界面化程序设计，如图4所示，为内啮合齿轮泵排量的计算和探究齿轮各参数对排量的影响都提供了便利。

4 排量验证

表1列举了3种不同型号规格的内啮合齿轮泵及其相关参数，其中型号Ⅰ的齿轮副传动类型为正传动，且变位后的实际中心距a′=10.84 mm；型号Ⅱ、Ⅲ的齿轮副传动为等变位传动，即啮合角与分度圆压力角相等，中心距没有变化。

图4 排量计算的程序显示面板

由于型号Ⅰ、Ⅲ的内啮合齿轮泵结构尺寸限制，内齿圈齿数较小，以及出于变位或齿顶修型的考虑，使内齿圈齿顶的部分齿廓不再是渐开线。但根据表1中相关泵的参数计算易知，这部分过渡圆弧齿廓极短，分别为0.35 mm和0.122 mm，故在对式(13)进行重合度计算时，可将其看作内齿轮齿顶圆与其基圆重合的情况考虑。基于上述条件并结合3种实际产品的参数信息，对本研究提出的排量精确计算式(9)进行实例验证所表1所示。

表1 内啮合齿轮泵排量的实例验证

表1中对应泵的型号和厂家分别是Ⅰ为国内海特克公司的PGI101-3-050型内啮合齿轮泵，Ⅱ为德国ECKLER公司的EIPH316高压内啮合齿轮泵；Ⅲ为德国VOITH公司的IPV-10型齿轮泵。根据排量的实际计算结果及其与公称排量的误差对比，充分说明了本研究介绍的分析方法的正确性，证明分析结果能够满足工程应用的需要。