基于等温活塞的空气压缩方法：多孔介质换热结构的优化

2019-11-18陈伟才

液压与气动 2019年11期

陈伟才

(1．北京航空航天大学自动化科学与电气工程学院，北京 100191；2．气动热力储能与供能北京市重点实验室，北京 100191； 3．中广核研究院有限公司，广东深圳 518031;4.北京机械工业自动化研究所有限公司，北京 100120)

引言

工业在我国能源消耗中占有绝对主导的地位，2017年全国总用电量为6307700 MWh时，其中工业用电量4362400 MWh，占全国总用电量的69%，比2016年增长了550 MWh。工业领域的节能也一直是我国政府节能工作的重点。

风机、泵类、空气压缩机是我国工业领域最主要的耗能设备，广泛应用于石油、化工、煤炭及矿产开采、电力等国民经济领域。据专家估计，这类产品的年耗电总量占全国总发电量的40%左右，配套电机容量约占电机额定年产容量的60%。风机、泵类、空气压缩机占工业用电的比例如图1所示[1-2]。

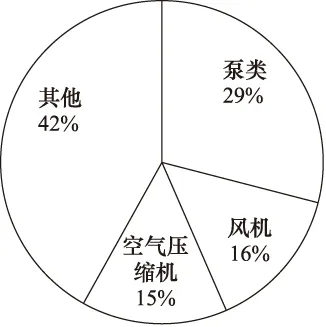
图1 工业用电分布图

其中，空压机作为工业产品类重要的能源，应用的范围及行业非常广泛，被称之为工业产品生产的“生命气源”。其中，活塞式空压机由于压力-流量特性比较稳定、价格低廉而受到广泛的应用。而在空压机的全生命周期成本中，初始采购成本仅占10%左右，而能源消耗成本却高达75%。在制备压缩空气的过程中，有50%的电力转化为压缩空气的有效能[3-4]。因此，节能降耗，提高运行效率成为空压机研究的当务之急。

根据空气的状态，压缩过程有3种：绝热压缩、等温压缩、多变压缩。工业应用的空压机普遍运行于接近绝热的多变压缩。图2是压缩时空气的p-V图，表示绝热压缩的功耗大于等温压缩。这是由于在绝热压缩过程中，产生高压气体时伴随产生大量的热，这就导致了压缩后空气温度的升高，空气压力在等温压缩的基础上，附加了温度上升而增加的压力，从而增加了压缩功耗。因此，空压机消耗的压缩功，取决于空气的温度以及空气的散热。

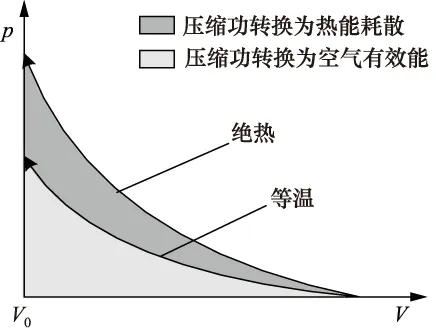
图2 绝热压缩，等温压缩p-V图

等温压缩空气储能技术是加强压缩空气与环境的热交换，将气体在压缩时温度的变化控制在一个较小的范围内，减少压缩功耗。目前，实现等温压缩的主要手段有2种：水雾冷却与液体活塞[5]。

1) 水雾冷却压缩技术

水雾冷却压缩空气技术是向压缩腔中喷入水雾，利用水滴与空气接触传热，带走压缩空气中的热量。水经雾化喷嘴高速喷出，形成雾化水滴[6]。但随着压缩缸内空气压力上升，喷嘴的背压增加，雾化的能耗将影响压缩机效率，图3为水雾冷却等温压缩原理图。

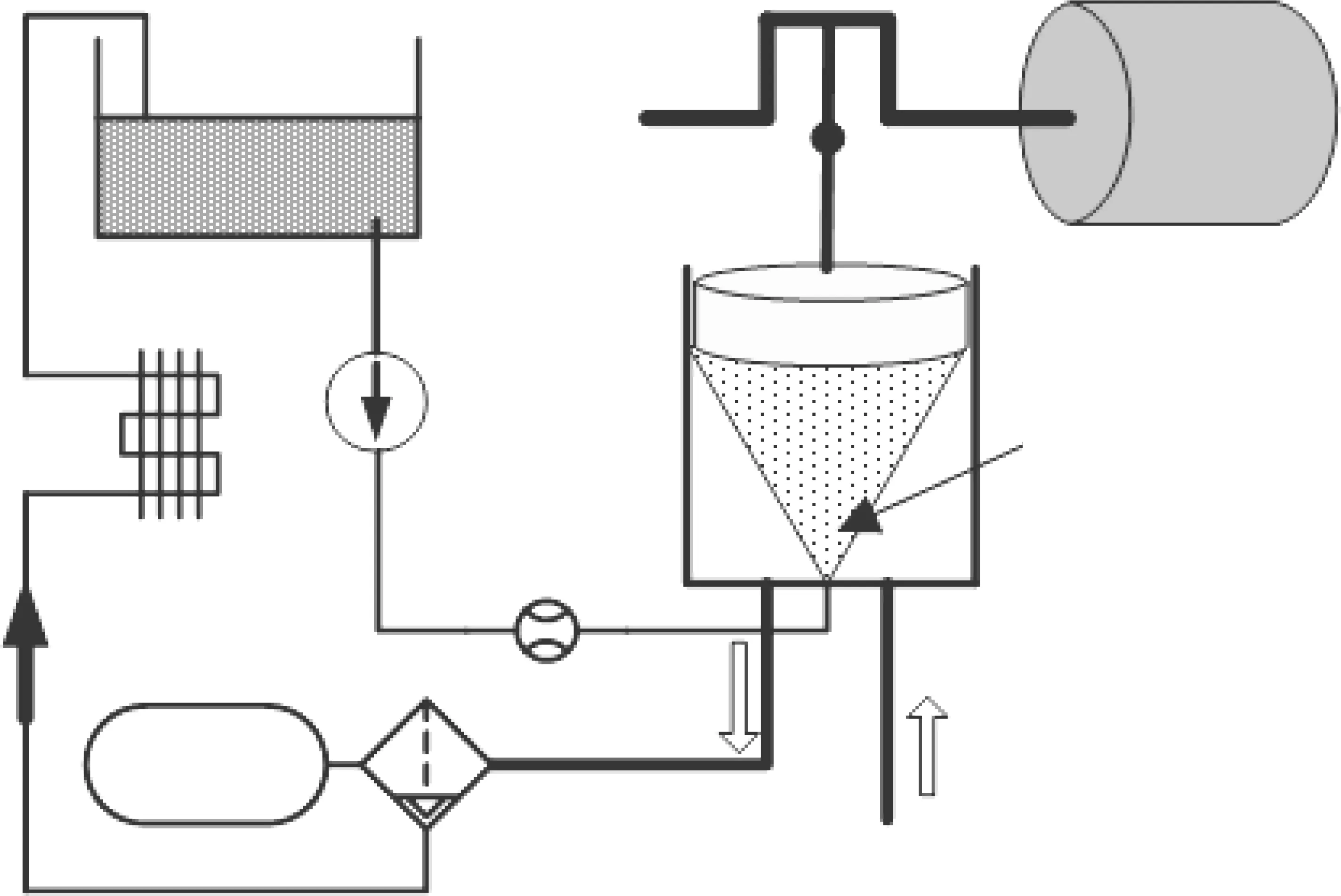
图3 水雾冷却等温压缩原理图

2) 液体活塞压缩技术

如图4所示，液体活塞压缩的基本原理是：电动机驱动液压泵，将液体压入容腔中，液体上升，压缩腔内空气的体积减小。压缩腔的下部而形成的上升的液-气界面实现压缩[7-10]。液体代替传热活塞，实现压缩空气，故称为液体活塞。

图4 液体活塞原理图

液体活塞的优势在于：

(1) 可适应不规则的容腔结构，实现密封，降低了压缩腔的加工要求，密封性要优于传统活塞；

(2) 黏性摩擦阻力要低于传统活塞；

(3) 液体活塞的活塞面积与容腔体积之比提高，可改善压缩空气的散热，液体作为中间介质向环境传递热量，这使得压缩过程接近等温，以提高压缩效率[11]。

液体活塞压缩仍存在一些问题需要解决。由于气体和液体在高压下直接接触，部分气体将溶解于液体，在液压系统中循环，将会降低液体弹性模量，增加液压泵和管路的噪声和振动，加剧磨损，以及在低压区域引起空化[12]。

1 等温活塞的提出

针对上述空压机面临的低效的问题，本研究基于等温容器和多孔介质技术，提出了一种等温活塞结构以实现等温压缩。

1.1 等温容器

等温容器是日本东京工业大学香川利春教授于1995年提出，是一种无论充气还是放气时容器内空气温度都基本不变化的特殊容器[13]。由于利用该容器的等温性质可以非常容易地产生和测量非定常流量，降低温度对测量的影响，这使得等温容器在气动系统设计和流量测量领域得到了广泛的应用[14-16]，图5为等温容器示意图。

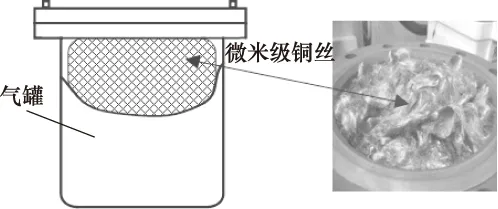
图5 等温容器

1.2 多孔介质

多孔介质材料具有复杂的三维立体结构，孔洞相互连通，使其具有了较大的比表面积和良好的流通性，当有流体流过孔洞时，一方面，多孔介质复杂的三维立体结构增强了对孔隙内流体的扰动，加强了对流换热；另一方面，大的比表面积使得多孔介质内具有极大的热交换面积。

因而，多孔金属泡沫材料具备了作为热交换材料的潜力[17]。

1.3 等温活塞结构

采用多孔介质传热和液体介质传热，形成气-固-液耦合的3层换热结构，利用多孔介质增大压缩空气与液体介质的换热面积，实现压缩热从气体向液体介质快速传递，液体介质经外部的散热器向环境散热。液体介质的热容远大于压缩空气，吸收压缩热后，温度基本保持不变。同时，使压缩空气的温度保持不变。

如图6所示，基于等温活塞的压缩系统由活塞、多孔介质、缸体、泵、散热器组成。空气在缸体中压缩，缸体下半部分存有液体。外部连杆驱动活塞上下运动。泵驱动液体在缸体和散热器之间循环。多孔介质的一端与活塞连接组成等温活塞，随活塞上下运动，另一端液体接触，缸体、泵和散热器串联形成散热回路。压缩过程产生的热，从气体传递至多孔介质，然后从多孔介质传递至液体。由于多孔介质的加入大大增加了气体与液体之间的传热面积，气体的温度趋近于液体。由于液体的热容远大于气体(1000倍)，液体吸热后，温度小幅上升。泵驱动液体在散热回路中循环，温度下降趋近于环境温度，因此，气体的温度也趋近于环境温度。

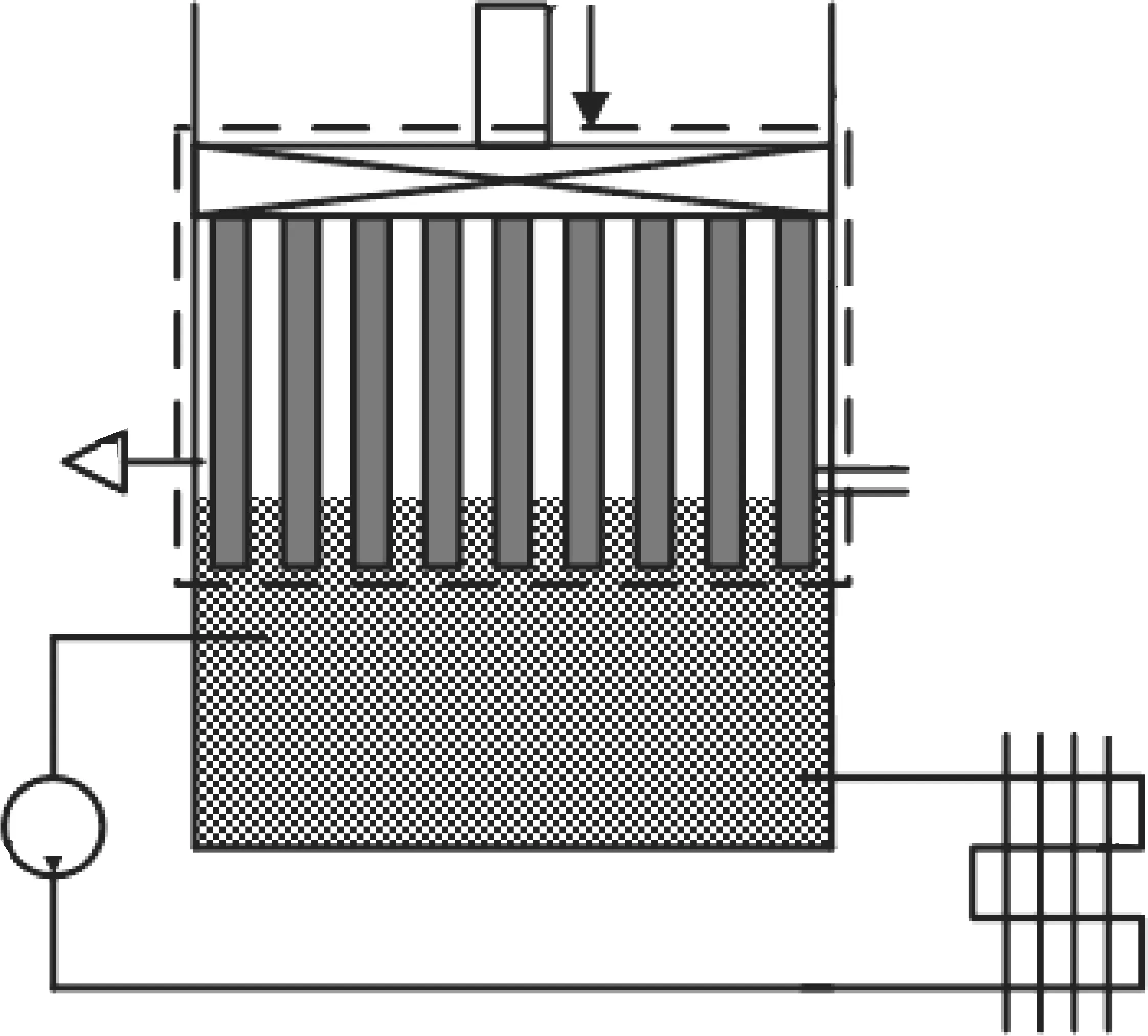
图6 等温活塞的原理图

多孔介质换热结构的引入增加气体传热的面积，以及对气相、液相进行扰动，加强流体的对流换热，但对活塞附加了流动阻力。增加多孔介质分布，将降低空气的温度。另一方面，增加多孔介质分布，多孔介质受到的液体和空气的流体阻力将增大。因此，本研究的主要工作是建立多孔介质结构参数与压缩功之间的关系，以及探索多孔介质结构参数优化的方法，为等温活塞的设计提供参考[18-20]。

2 数学模型

2.1 压缩基本方程

对于闭口系统，根据能量守恒定律可知，外界传入系统的热量和功等于系统内能的增量，即：

dU=δQ-dW

(1)

式中， dU—— 系统内能的增量

δQ—— 外界传入系统的热量

dW—— 外界对系统所做的功

以气缸内部气体为对象，活塞的压缩功转换成气体的内能及向多孔介质的传热。将能量方程式(1)应用于压缩空气可得：

dUair=-δQ+dW

(2)

式中， dUair—— 气体的内能

2.2 传热模型

根据牛顿冷却定律，物体1与物体2之间的传热与传热面积和两物体之间的温差(T1-T2)成正比，即：

δQ=hS(Tair-Tpor)dt

(3)

式中，h—— 传热系数

S—— 传热面积

Tair—— 空气温度

Tpoor—— 多孔介质温度

压缩时，活塞向下运动，部分多孔介质浸入水面以下，水面上方与空气接触的多孔介质面积减小，即，传热面积随压缩空气体积的减小而减小[21-22]。

2.3 多孔介质几何模型

多孔介质内部结构复杂，数值模拟计算时需要根据其结构特征简化几何模型。常见的多孔介质几何模型有：面心立方、体心立方、八面体、十四面体等。

多孔介质制作工艺使生成的多孔介质材料，具有面心立方的特征[23](FCC，即face-centered-cubic)，工程中多采用面心立方体模型计算多孔介质的阻力。如文献[24]中就采用面心单元模型构建了多孔介质几何模型。文献[25]中采用面心单元模型进行了力学分析。

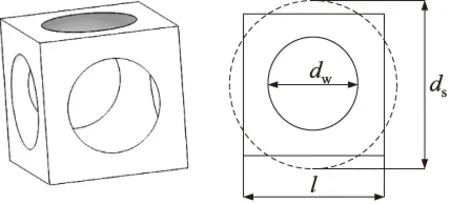
图7 面心立方体单元及其中心横截面

根据几何关系可得孔隙率和比表面积的表达式如下：

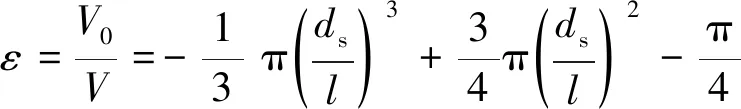
(4)

(5)

式中，ε—— 孔隙率

V0—— 面心立方体的空隙体积

V—— 面心立方体的表观体积

ds—— 球体直径

l—— 面心立方体的单元边长

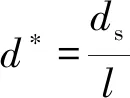
2.4 阻力模型

流体流过多孔介质时，流体产生的压力梯度Δp/L与多孔介质结构参数相关，Ergun基于均匀球形颗粒层床模型，提出了经典的Ergun方程[26]：

(6)

式中， Δp/L—— 压力梯度

u—— 流体流速，m/s

μ—— 流体黏性系数，kg/(m·s)

a—— 黏性项常数，a=150

b—— 惯性项常数，b=1.75

ρ—— 流体密度，kg/m3

dp—— 球形颗粒直径，m

Ergun方程适用于球形颗粒介质结构，本研究讨论多孔介质具有面心立方体结构。参考文献[27]在阻力等效的基础上，建立了面心立方体结构与球形颗粒结构的对应关系。

根据该对应关系就可以将面心立方体结构的孔径转换成等效的球形颗粒直径，代入Ergun方程，得到多孔介质受到的阻力。

文献[24]中基于面心立方体几何模型，采用CFD流体计算方法进行阻力的计算，并用实验对CFD流体计算方法验证，压力梯度误差约为6%，验证了采用该CFD方法可以用于分析多孔介质的阻力。

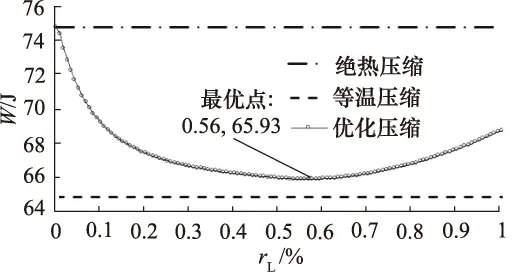
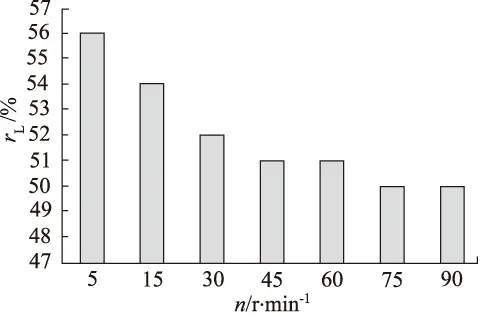
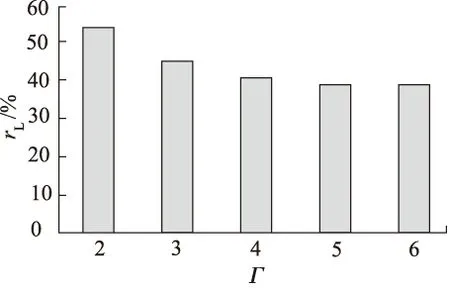
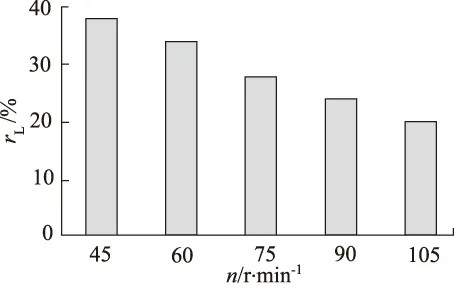
文献[27]采用上述CFD方法，对上述基于面心立方体结构的Ergun方程进行验证，在40

因此，本研究基于上述面心立方体模型的Ergun方程进行阻力计算。

3 多孔介质结构参数优化方法

3.1 目标函数

优化的目标是使压缩功和流体阻力做功最小，即，压缩总功耗W最小。

(7)

式中，p—— 压强

Δp—— 压强变化量

V0—— 压缩腔体积

V—— 压缩后空气的体积

3.2 问题描述

根据式(6)，当多孔介质的长度L增加时，流体的阻力及其阻力做功增加，传热面积增加，压缩功减小。因此，多孔介质的长度L与总功耗关系不是单调的，后续章节将研究长度与总功耗的关系。

3.3 长度L寻优

对于不同排量的压缩机，压缩腔内空气柱长度的设计会发生变化，为使下述讨论推广至所有压缩机，定义多孔介质长度比rL：

(8)

式中，Lair—— 初始时刻压缩腔空气柱长度(120 mm)

L—— 多孔介质的长度

参数优化是指以1 mm为间隔，在0～120 mm范围内，遍历120种长度值，找到最小压缩功对应的多孔介质长度比rL的取值，并研究不同情况下的长度比。

4 仿真结果分析

本研究采用的压缩腔直径为100 mm，活塞的行程为60～120 mm。以该压缩机为例(参数见表1)，研究不同条件(压缩比和转速)下，多孔介质长度的取值与压缩做功、阻力做功的关系。首先，令压缩比Γ为2，讨论转速对多孔介质长度的影响。在压缩比Γ为2时，绝热压缩功耗为74.77 J，等温压缩功是64.88 J，因此，实现等温压缩，压缩机的节能空间为9.89 J。

由图8～图10可知，在不同压缩机转速条件下，多孔介质长度比对压缩总功耗的影响，长度比与总功耗的关系非单调。图11表示总功耗取最小值时，多孔介质长度比随着转速的增加而变短。随着转速的增加，阻力做功对总功耗的影响增大。

图8 n=5 r/min时，多孔介质长度比与总功耗的关系

表1 仿真参数表[28-29]

图9 n=30 r/min时，多孔介质长度比与总功耗的关系

图10 n=90 r/min时，多孔介质长度比与总功耗的关系

图11中显示随着转速增加，多孔介质长度的取值逐渐减小。图12中显示随着转速增加，阻力做功先增大后减小。由式6可知，阻力做功随多孔介质长度减小而减小，随速度的增大而增大，因此，决定阻力做功的因素有两个：多孔介质长度比和转速。图12说明，转速较低时，转速对阻力做功的影响起主要作用；转速较高时，多孔介质长度比对阻力做功的影响起主要作用。

图11 压缩比Γ=2时，转速对多孔介质长度比的影响

图12 压缩比Γ=2时，转速对总功耗的影响

图12中显示随着转速增加，压缩做功单调增大。一方面，多孔介质长度比随转速的增加而减小(图11)，换热面积减小；另一方面，转速增加，每个压缩周期内换热时间减小，换热面积和换热时间减少两个方面使换热效果变差，从而引起压缩做功的增加。压缩做功在总功耗中的占比大，因此，总功耗的变化趋势与压缩做功变化趋势相近。根据式(9)，得到节省做功百分率α曲线，表示随着转速的增加，节能的效果变差。

节省做功百分率α的定义：

(9)

式中，W—— 实际做功

Wj—— 绝热做功

图13展现的是速度一定时，压缩比Γ与优化后多孔介质长度比rL的关系。多孔介质长度比随着压缩比Γ的增加而下降。随着压缩比Γ的增加，活塞行程将增加，多孔介质浸入水中部分的长度增加，根据式(6)，阻力做功增加，且增加量大于压缩做功的减少量。当压缩比大于5后，增加单位压缩比，活塞行程的增量不明显(小于1/(30×Lair))，即，对阻力做功影响变小，因此，多孔介质长度比取值逐渐趋近于39%，称此值为多孔介质长度比rL的收敛值，表示压缩机取高压缩比时(大于5)，优化后多孔介质长度比rL的取值。图14表示转速与多孔介质长度比的收敛值之间的关系。随着速度的增加，收敛值逐渐减小。