双锻造操作机大车行走系统控制方法探析

2222

(1.燕山大学 机械工程学院， 河北 秦皇岛 066004；2.燕山大学 河北省重型机械流体动力传输与控制实验室， 河北 秦皇岛 066004)

引言

锻造操作机是锻造车间内的重要辅助操作装备，主要用于夹持锻件配合主机完成各种锻造工艺，操作机的使用极大地提高了锻造效率[1-2]。随着《中国制造2025》的全面实施，大型优质高精锻件在国民经济各行业的需求逐渐凸显，对现有的自由锻造模式提出了新的要求[3]。2017年，全球最大的锻造操作机生产商Dango & Dienenthal公司发布了双锻造操作机夹持锻件进行联合锻造的视频[4]，这标志着自由锻造行业又将进入了一个新的发展阶段。与单操作机锻造生产线相比，双操作机锻造生产线具有自动化程度更高、生产节拍更快、锻件尺寸更精等优势，尤其适合于高精长轴类锻件和锻造温度区间窄的有色金属锻件的锻造[5-7]。然而，双操作机夹持高温锻件构成的系统更加复杂，负载的大惯性迟滞、机液和刚柔系统的强非线性以及耦合等特点，给双锻造操作机系统的安全可靠控制带来了巨大挑战。目前，国外关于双锻造操作机系统控制的研究鲜见，国内大多学者的研究重心主要在单机方面，且以机构构型设计为主[8-14]。锻件的轴向进给是自由锻造过程中的重要工序，双操作机夹持锻件进给是在两台设备大车行走系统共同驱动下完成的，双机系统的稳定性和控制精度直接影响锻件质量和生产效率，因此研究双锻造操作机大车行走系统的控制方法具有重要意义。

双锻造操作机大车行走系统的控制涉及两台设备的同步问题，实现双机同步的控制方法主要有主从控制和等同控制两种[15]。主从控制方式是指在两台设备中，一台设备作为主动方进行主要控制，另一台作为跟踪方跟随主动方的运动而实现同步。主从控制方式的同步误差取决于从动设备的跟随特性，对于大惯量和非线性系统而言，会产生较大的响应滞后和交互耦合影响，因此不适用于双锻造操作机大车行走系统的控制。等同控制方式是指对两台设备分别同时给定相同的期望信号，各设备同时跟踪理想给定信号而达到同步目的。等同控制方式的同步误差仅来自于两执行器的动态响应差异，相比于主从控制方式，更适合于双锻造操作机大车行走系统的控制，但两台设备的交互耦合仍然影响双机系统的控制特性。

因此，以燕山大学在建的“5 MN快锻油压机中试平台”中的两台20 kN锻造操作机为研究对象，针对双操作机大车行走系统的控制问题展开研究，探索其同步控制方法，旨在为双锻造操作机智能化锻造提供技术支撑和理论指导。

1 双操作机大车行走系统介绍与数学建模

1.1 双操作机系统介绍

双锻造操作机系统组成如图1所示，左右两台操作机A和操作机B分别置于锻件两端，通过夹钳实现锻件的双边夹持。与生产设备不同，作为试验样机，燕山大学的两台20 kN锻造操作机在液压和机械系统方面采用了不同的配置，大车行走系统的部分参数如表1所示。

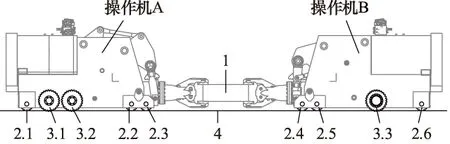
1.锻件 2.承重轮 3.驱动轮 4.轨道

从表1可以看出，操作机A大车行走系统采用了2组4个低速大扭矩马达驱动，而操作机B则采用了1组2个高速马达驱动。在液压系统压力、操作机重量、驱动轮、承重轮等方面两台设备基本相同。但由于驱动液压系统和相关元件的变化，导致两台设备的动力性能产生较大差异，经计算操作机A的大车行走理论最大加速度约1650 mm/s2，而操作机B的大车行走理论最大加速度约2500 mm/s2，动力性能的差异更增加了双机系统控制的难度，同时也更具有典型性。

表1 锻造操作机A/B的主要技术参数

1.2 双操作机大车行走系统数学模型

不考虑中间夹持锻件的弹性变形，双锻造操作机大车行走系统的受力分析如图2所示。K1，K2和B1，B2分别表示操作机吊挂机构[9]的机液耦合系统等效弹簧刚度和等效阻尼。

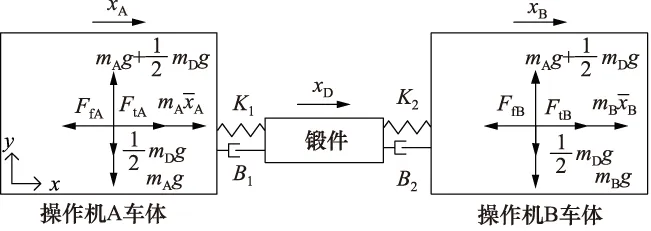
图2 双操作机大车行走系统受力分析

操作机A的力平衡方程为:

(1)

操作机B的力平衡方程为:

(2)

锻件的力平衡方程为:

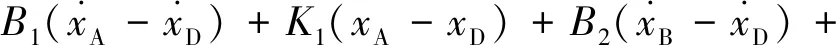
(3)

式中,FtA,FtB—— 操作机A、B行走驱动力，N

FfA，FfB—— 操作机A、B行走摩擦力，N

xA，xB—— 操作机A、B行走位移，m

mA，mB—— 操作机A、B质量，kg

xD—— 锻件行走位移，m

mD—— 锻件质量，kg

两台锻造操作机大车行走液压系统采用的是传统的阀控马达系统，数学建模过程不再赘述，详见参考文献[16]。综上，建立双操作机大车行走同步控制系统数学模型如图3所示，同时设定下文仿真所需主要参数，如表2所示。

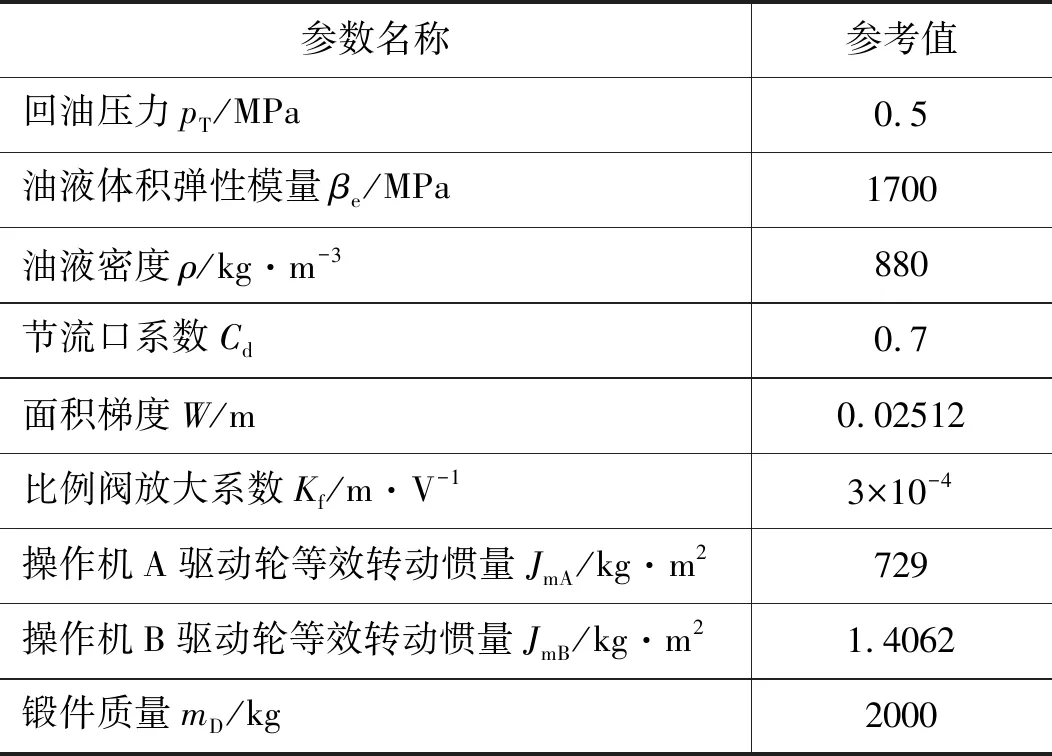
表2 仿真参数设置

图3 双锻造操作机位置同步控制系统数学模型

图4 双操作机独立反馈位置同步控制框图

2 双操作机独立反馈位置同步控制仿真分析

实际锻造系统中，锻件的位置难以直接检测，锻造操作机大车行走的位移主要通过行走马达转角控制，进而实现对锻件位置控制。采用等同控制方式，分别给定两台操作机相同的位移，建立双操作机系统独立反馈位置同步控制框图，如图4所示，大车行走的马达转角通过旋转编码器检测并反馈到系统进行闭环控制。

图4双操作机独立反馈位置同步控制框图控制器采用PID控制，优化控制器参数，最终设置控制器1中P=0.9、D=0.05，控制器2中P=3，D=0.005。仿真结果如图5所示。

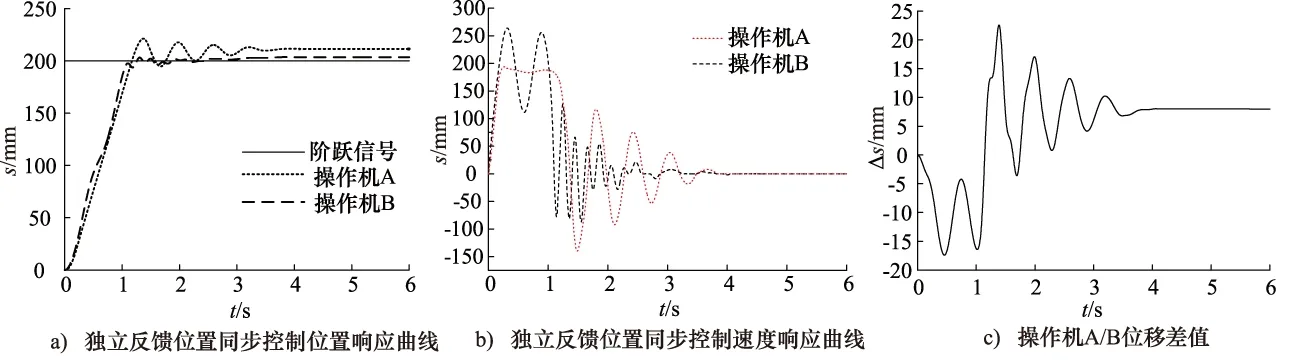
图5 独立反馈位置同步控制仿真曲线

图6 双操作机位置速度复合独立反馈同步控制框图

可以看出，阶跃给定时，操作机A和操作机B的同步效果极差。起动阶段，操作机B的快速性优于操作机A，操作机B快速起动，位移差值最大约16 mm左右。在弹簧阻尼的交互耦合作用下，两台设备中期某时刻可以获得瞬时的同步，随后的制动阶段，操作机B由于其高制动能力，位移超调量较小，但操作机A的制动能力差于操作机B且出现了严重超调现象，因此两台设备又产生较大的同步误差，最大位移差值接近22 mm。在实际锻造生产过程中，如此大的位移差极易导致系统的振荡而发生失稳，另外由同步误差引起的耦合作用力也会作用在高温锻件上，使锻件发生变形或弯曲。

3 双操作机位置速度复合独立反馈同步控制仿真分析

锻造操作机系统的惯性极大， 在运动过程中位移变化是连续性的，所以直接给定跳变的阶跃信号是不合理的，极易造成系统的冲击、振荡甚至失稳。纵然调节PID参数以减小超调振荡，但同时会牺牲系统的快速性。另外，双操作机独立反馈位置同步控制效果差的原因是两台设备的动力性能差异较大，因此限制操作机B的动力性能发挥，采用位置速度复合方式对双操作机大车行走系统进行控制，控制框图如图6所示。

图6中专门设计了位置速度轨迹规划发生器，其目的是使两台动力不同的设备产生同样的轨迹规划期望曲线。位置速度轨迹规划发生器输入的是位移和加速度值，经计算后获得平滑位移和速度曲线，如图7所示。以此作为操作机A和操作机B的输入信号。操作机A的速度与旋转编码器转角微分并转化后进行比较，差值输入控制器1。操作机A的位移与旋转编码器转角直接比较，输入控制器2。操作机B采用同样的方式进行控制。

图7 轨迹规划期望曲线

在其他参数不变情况下，采用位置速度复合独立反馈同步控制的仿真曲线如图8所示。可以看出，操作机A和操作机B的同步控制效果较独立反馈位置同步控制效果好很多。首先，系统的快速性提高，位置速度复合控制的响应时间约0.8 s，而位置独立控制的响应时间约1.2 s，快速性提高了33%。其次，两台设备的同步误差大大减小，位置速度复合控制方法在双机动态过程中最大误差为16.8 mm，基本不存在稳态误差。从两台设备的速度曲线可以看出，操作机A和操作机B的速度与规划曲线规律一致，且误差较小，从而避免了系统振荡失稳发生的可能性。

4 双操作机基于位置速度复合控制的状态差值校正同步控制仿真分析

基于独立反馈位置同步控制方法， 利用位置速度轨迹发生器实现了双操作机大车行走系统的复合控制，基本解决了两台操作机动力性能差异的问题，但是不能顾及双机耦合因素或外部干扰对系统同步控制的影响。当一台设备由于扰动因素出现位置偏差时，另一台设备继续跟随期望曲线，不能做出相应的协调反应，必然导致同步误差增大，锻件承受较大的耦合力。因此在位置速度复合独立反馈控制策略的基础上，引入状态差值校正环节，建立控制框图如图9所示。状态差值是指两台操作机行走马达同步行走过程中实时的位移误差。通过旋转编码器分别检测操作机A和B行走马达转角，作差后得到状态差值，输入控制器5得到校正信号，然后反馈输入到控制阀。

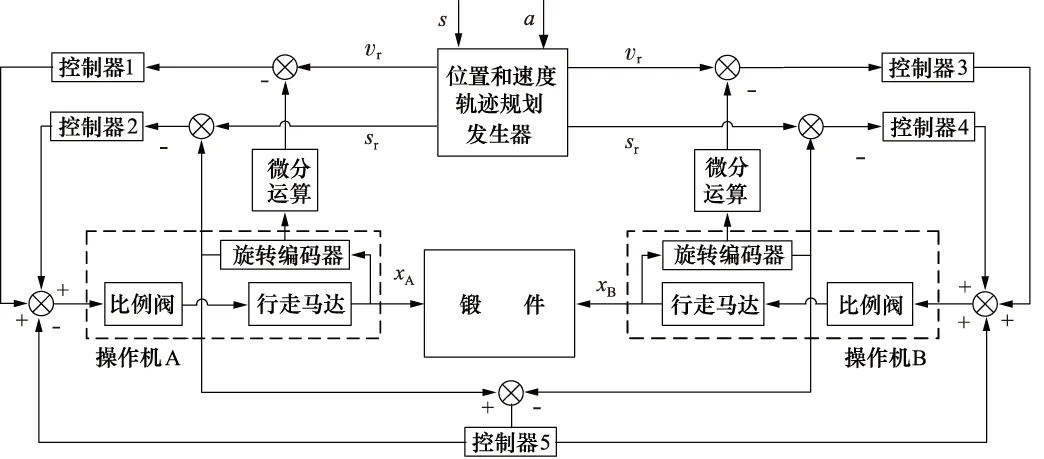
图9 双操作机基于位置速度复合控制的状态差值校正同步控制框图

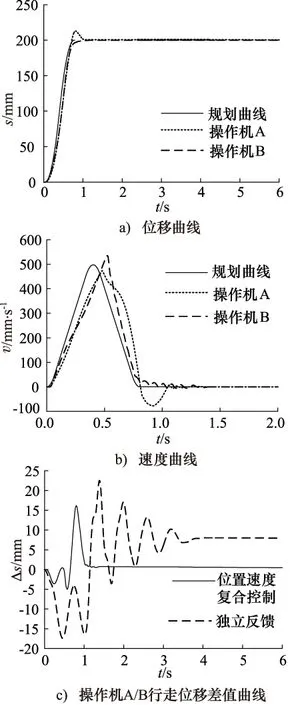
图8 位置速度复合独立反馈同步控制仿真曲线

设定状态误差校正控制器5的参数为P=10，D=0.5，在分别给定轨迹规划发生器加速度为1650, 1300, 1000 mm/s2的条件下进行仿真，仿真结果位移曲线如图10所示，速度曲线如图11所示。

图10 不同加速度下的状态差值校正同步控制位置曲线

图11 不同加速度下的状态差值校正同步控制速度曲线

可以看出，状态差值的误差补偿效果使两台操作机的行走位移曲线和速度曲线更加吻合，而且随着给定加速度的减小，双机同步效果越来越好，行走位移曲线的超调现象消失，速度曲线更加贴近于速度规划曲线，主要是因为操作机A的动力性能逐渐可以满足给定加速度的要求，可控性增强。在图10a行走位移曲线的制动阶段，操作机A与操作机B出现同时超调现象，由于操作机B具有更强的动力性能和更好的可控性，在状态差值校正的作用下使操作机B的行走曲线向具有超调响应的操作机A行走曲线贴合。由此可见，想要获得好的同步控制效果势必要减小给定加速度的值。当给定加速度值减小到1000 mm/s2时，双机的响应时间为1.05 s，无超调现象，其同步误差曲线如图12所示，误差范围在[-0.28 mm,0.02 mm]内，满足双锻造操作机的同步行走控制要求。

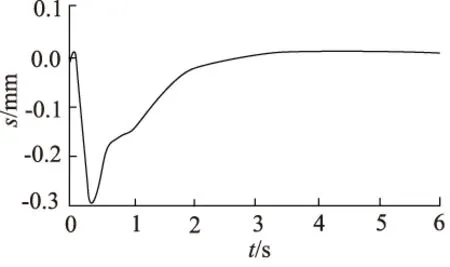
图12 操作机A/B行走位移误差曲线

5 结论

为实现双锻造操作机大车行走系统的同步位置控制，以燕山大学两台20 kN锻造操作机为对象，搭建了双锻造操作机行走系统数学模型，在此基础上仿真分析研究了3种不同控制方法对双操作机大车行走系统控制特性的影响，结论如下：

(1) 当两台设备动力性能差异较大时，独立反馈位置同步控制的双操作大车行走系统具有较大的同步误差，系统的稳定性差；

(2) 利用位置和速度轨迹规划发生器可得到光滑的期望轨迹曲线，在此基础上采用位置速度复合独立反馈控制方法提高了双操作机大车行走同步系统的快速性和稳定性；

(3) 综合考虑双操作机大车行走系统的耦合影响，采用位置速度复合的状态差值校正同步控制方法效果最好。仿真结果显示，设定两台操作机加速度均为1000 mm/s2，双操作机大车同步行走200 mm位移时，系统的响应时间为1.05 s，同步位置误差范围为[-0.28 mm,0.02 mm]，满足双锻造操作机的同步行走控制要求。