基于多时相Sentinel-1SAR地表土壤水分反演的Alpha近似模型改进*

陈婷婷 潘耀忠 孙 林

（1 山东科技大学测绘科学与工程学院，山东 青岛 266590）

（2 遥感科学国家重点实验室(北京师范大学地理科学学部)，北京 100875）

（3 环境演变与自然灾害教育部重点实验室，北京师范大学地理科学学部，北京 100875）

土壤水作为地表水存储的重要组成部分，不仅直接影响着陆地和大气间的物质和能量交换，而且是水文模型、气候模型、生态模型以及陆面过程模型的关键输入参数［1］。土壤水分监测方法从数据获取方式上分为基于站点的土壤水分观测、基于气象数据和基础地理数据的土壤水分模拟与同化，以及基于遥感数据的土壤水分反演［2］。站点测量土壤水分的测量深度和精度均比较高［3］，但是由于土壤水分的时空异质性，站点观测并不能完全表征区域内的土壤水分变化［4］。基于气象数据和基础地理数据驱动、利用模型模拟的土壤水分尽管在时空尺度上有连续性，但模拟精度极大程度上依赖于参数化方案和参数化过程的选择，参数繁多较难实用。遥感技术直接以面的形式对地表进行大面积同步观测，其监测范围不受站点分布位置的限制［5］，为土壤水分的动态监测提供了有效的方法［6］。

遥感反演土壤水分分为光学和微波遥感两种。其中可见光—近红外方法主要依赖于地物的反射光谱特性，由于受云及太阳光照射条件的限制，可见光、近红外等光学遥感方法对土壤水分的研究存在一定的局限性［7］。微波遥感通过探测土壤的介电属性变化监测土壤水分信息，而土壤介电常数与土壤水分密切相关；且微波遥感不受太阳辐射的影响，大气的影响微乎其微，具有全天候、全天时的优势，从而逐渐成为监测土壤水分的一种有效手段。

微波遥感反演土壤水分主要分为主动和被动微波遥感两种，被动微波遥感重复观测频率高，且被动微波辐射信号对介电属性较表面粗糙度更为敏感，因而对地表特征要求不高，但其监测空间分辨率低，适于大尺度调查。与之相比，合成孔径雷达（Synthetic Aperture Radar, SAR）具有更高的空间分辨率（1 m～1 km），可以获取较大范围更为精细尺度上的土壤水分信息［8］。主动微波探测土壤水分的主要难点在于，土壤表面的后向散射系数强度与土壤水分之间并非呈简单的线性关系，它除了与土壤水分含量有关外，还与土壤物理特性（结构、成分）、植被（数量、结构）以及雷达系统参数相关。因此，土壤水分的反演在本质上属于“病态”问题，雷达后向散射系数和土壤水分之间的关系必然存在着不确定性。为降低这种不确定性，可借助于多种观测模式（多极化［9-11］、多角度［9,12］、多波段［13-14］）的数据或者多源数据（被动微波［15-16］、光学遥感［14,17］）来反演土壤水分，但是多种观测模式或者多源的观测数据通常难以获取。

已有的研究表明，利用重复观测的SAR数据进行土壤水分反演具有较大的潜力。多时相土壤水分反演方法基于以下假设，在观测期内，地表粗糙度和植被相较于土壤水分变化缓慢（不考虑耕作的发生），从而可将其忽略，并假定时间序列的雷达后向散射系数的变化仅由土壤水分的变化造成，该方法适于裸土及低植被覆盖区域［18-20］。Wickel等［21］使用一个月内获取的10景Radarsat影像对收割后的小麦地进行土壤水分监测，结果表明后向散射系数σ0的变化与土壤水分的变化存在较好的相关性（R2=0.89）；Kim等［22］利用多期观测数据建立成本函数,通过最小化成本函数在预先建立的查找表中得到多期土壤水分的解，反演结果与地面实测数据有较好的相关性;Balenzano等［23］基于上述假设提出了Alpha近似模型，采用两个时相雷达后向散射系数的比值将粗糙度、植被覆盖和土壤水分对后向散射系数的影响进行解耦，并构建观测方程组反演得到每期的土壤水分值，研究表明，利用HH极化数据反演的土壤水分精度可以达到0.05 m3∙ m-3。该方法为利用时间序列SAR数据反演土壤水分提供了一种新思路，He等［24］对Alpha算法进行了扩展，在求解观测方程组的过程中，通过使用Juxtaposition方法自适应确定土壤水分的上下界，不再依赖于地面实测数据；Ouellette等［25］使用L波段机载雷达数据将Alpha模型应用于植被覆盖区域的土壤水分反演，并将观测方程组扩展到多极化（HH和VV），结果表现出较好的适用性；Zhang等［26］针对观测方程组欠定问题，通过融合多源时序SAR数据增加了有效观测方程，从而实现观测方程数大于未知数个数，提高了土壤水分反演的可靠性。

影响雷达回波强度的因素可分为雷达系统参数和地表特性，前者包括频率、极化方式、入射角等，后者包含地表的物理特性以及几何特性。在雷达系统参数确定的情况下，雷达回波强度主要与地表特性相关［7］。Alpha近似模型将两个时相雷达后向散射系数的变化归结为土壤水分的变化，这要求前后期的雷达观测系统参数一致或者变化较小。然而在实际情况中，当雷达观测系统确定后，频率、极化方式随之确定，入射角会有发生变化的情况，特别是在不同轨道过境时获取地面影像。由于自然界大多数地表并不完全是粗糙的朗伯表面，其反射并非各向同性，因此同一地物在不同入射角下得到的后向散射会表现出差异。在应用Alpha近似模型时，如果两个时期雷达观测的入射角不同，那么后向散射系数的变化也包含来自入射角变化的影响。针对上述问题，本文提出改进的Alpha模型，将时间序列SAR数据的入射角的变化考虑进来，选取了两个典型实验区：我国黑河流域的农田区域和加拿大曼尼托巴省农田区域，利用欧洲太空局 (European Space Agency, ESA) “哨兵系列”的雷达卫星Sentinel-1数据及对应区域的土壤水分观测网络数据对算法进行验证，并对结果进行分析与讨论。

1 材料与方法

1.1 实验区概况

本文所选实验区均位于农田区域，地表在作物收成之后一段时间处于裸露状态，土壤水分反演可不考虑耕作对土壤粗糙度的影响及植被覆盖的影响；地形较为平坦，因此地表起伏对雷达后向散射系数的影响也可忽略；此外均有长时间序列的站点观测数据对土壤水分的反演结果做验证支持。实验区1位于我国黑河流域(100°10′～100°30′E，38°45′～38°55′N)，属大陆性温带干旱气候；其中游属于农业经济区，也是西北地区重要的商品粮基地。实验区2位于加拿大的曼尼托巴省温尼伯市(98°30′～97°W，49°～50°30′N)，地处北红河与阿西尼泊因河交汇的广阔平原，北部紧邻温尼伯湖，气候属温带大陆性气候。

1.2 雷达数据与处理

Sentinel-1是欧洲航天局哥白尼计划（GMES）中的地球观测卫星，由A、B两颗星组成，主要服务于陆地和海洋监测，由欧空局（European Space Agency，ESA）组织研发。本文所用数据为干涉宽幅模式（Interferometric wide swath，IW）下经过多视处理和地距转换的GRD格式产品。利用SNAP软件对雷达影像进行预处理，主要包括热噪声去除、轨道文件校正、辐射定标、滤波校正、多普勒地形校正，最终获得入射角和后向散射信息。表1给出了本文所用黑河和温尼伯实验区各期时序Sentinel-1影像的具体信息。以黑河实验区为例，当卫星按相同的方向且以同一轨道过境时，雷达波束的入射角不变，如2016-11-07和2016-12-01获取的影像，站点平均入射角均为43.7°；当卫星过境方向或者轨道发生变化，则入射角随之改变，有的变化较小，如2016-11-07和2016-11-13获取的影像，有的变化较大如2016-12-07和2016-12-14的影像，相对于整个时间序列的Sentinel-1影像入射角发生了10°左右的变化，当角度变化较小时其对后向散射的影响可忽略不计，而当角度明显变化时其影响将不能忽略，Alpha近似模型的应用会受到影响。

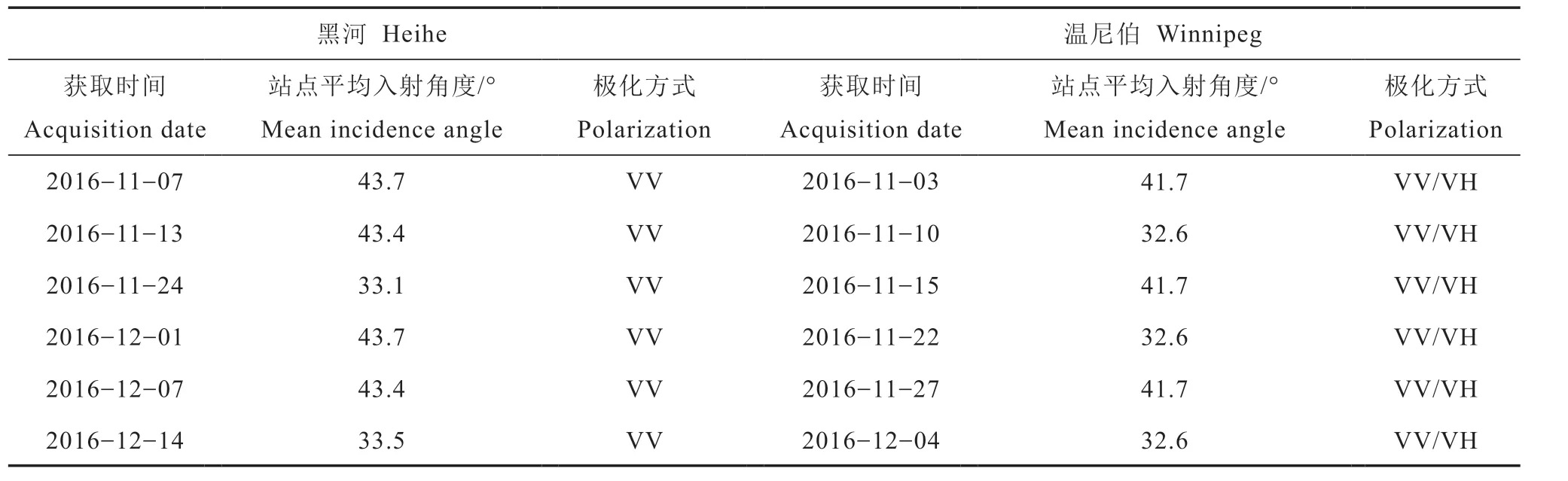
表1 实验区Sentinel-1 数据Table 1 List of Sentinel-1 SAR images of the experiment areas

1.3 地面数据

黑河流域实验区所用地面数据来自黑河生态水文遥感试验（Heihe Watershed Allied Telemetry Experimental Research，HiWATER）。本文所用数据包括黑河流域中游张掖市的三个站点的数据［27-28］，分别位于大满、党寨和花寨子，土地类型分别为农田、草地和荒漠。以上站点均提供全年逐日逐时（每10 min）不同深度（2 cm、4 cm、10 cm等）的土壤水分含量（%）、土壤温度（℃）数据，本文使用其中4 cm深度的土壤数据，根据Sentinel-1影像的获取时间选择与其最接近时刻的观测数据作为实测值；土壤质地、土壤容重数据来自2012年黑河流域土壤参数观测数据集，其中位于党寨的站点没有相应土壤质地数据，以花寨子的数据代替。

加拿大曼尼托巴省实验区的地面数据来自于RISMA(Real-time In-situ Soil Monitoring for Agriculture)土壤水分观测网络［29-31］，由加拿大农业和农业食品部（Agriculture and Agri-Food Canada’s, AAFC）于2011年组织建立。本文所用12个监测站点的数据其中有9个位于温尼伯市西南部的农田区域，3个位于温尼伯市西北部的农田区域，每个站点均提供观测期间不同深度（0～5 cm、5 cm、20 cm等）的土壤水分（%）、土壤温度（℃）数据，并且每个深度均布设了3个探头。本文使用其中5 cm深度的土壤数据，选择与卫星过境时间最为接近时刻的观测数据作为实测值，对于3个传感器的观测值本文取其平均；对于土壤质地、土壤容重，本文以世界土壤数据库HWSD（V1.2）提供的1 km网格数据作为参考。

1.4 理论与方法

微波散射理论模型是通过建立后向散射系数与地表物理和几何参数间的数学关系来研究粗糙表面的散射，以求解介电常数和土壤水分。小扰动模型SPM［32］是研究小尺度粗糙度表面的经典模型，其一阶形式描述的是面散射，二阶形式为体散射。由于大多数自然地表面散射占主要成分，因此常用其一阶形式。以垂直极化VV为例，随机粗糙表面的后向散射系数可以表示为［33］：

式中，k表示雷达波数，表达为：k=2π/λ，h为均方根高度，θ为入射角，εr、μr分别为介电常数和磁导率，W为表面粗糙度谱函数。当磁导率取值为1时，上式可简化为：

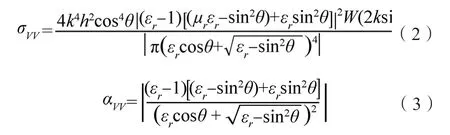
式中，αVV为极化幅度，是雷达入射角度和介电常数的函数。因此式（2）可进一步表达为：

在低植被覆盖情况下，假设植被参数对雷达后向散射的影响是乘性的，即在上式的基础上乘植被衰减因子。假定地表粗糙度和植被状况在一定时间内是不变的，只考虑土壤介电常数（主要受土壤水分影响）的变化，则将两个时间观测的后向散射系数作比值处理，不考虑入射角的变化，化简后可得到式（5），即为Alpha近似模型［23］。

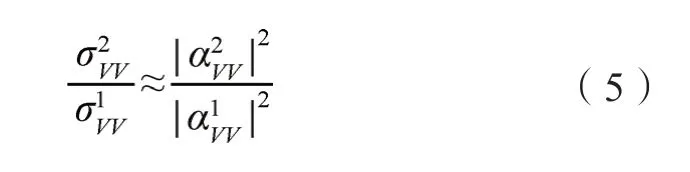
当时间序列SAR数据入射角变化较大时，跟入射角有关的各项将不能抵消，式（5）已不再成立。由于粗糙度谱函数主要是一个地表粗糙度相关的参数（表面相关长度），因此本文只考虑了与入射角直接相关的乘积项cos4θ，从而得到改进的Alpha模型如式（6）。

基于两个时相的SAR数据，根据式（6）可得到观测方程：

对于连续N期SAR影像（T1、T2、T3，…，TN），可以构建N-1 个有效观测方程，组成如下方程组：

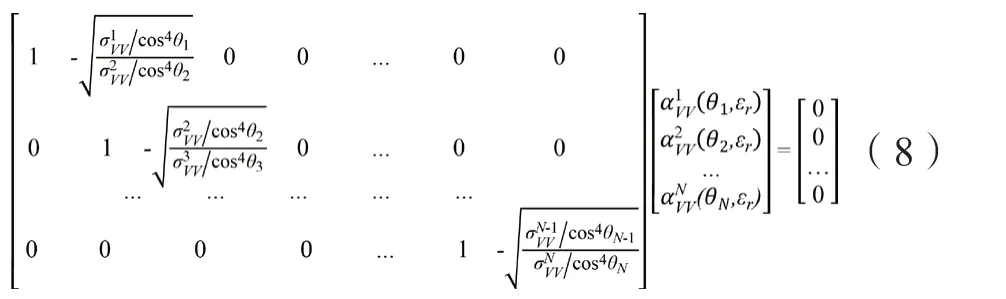
对于方程组（8），N-1方程中存在N个极化幅度未知数，是一个欠定方程组，存在无数多个解。可采用边界约束的最小二乘法进行求解，根据实际的雷达入射角度和土壤水分范围对αVV取值范围进行限定。本文黑河实验区所用站点分别位于不同的土地覆盖类型区，曼尼托巴省的站点分布于不同区域的农田之中，因此每个站点各自设定αVV边界。得到极化幅度αVV后，进而根据式（3）求得土壤的介电常数εr，最后利用介电混合模型［34］求得土壤水分mV。

2 结果与讨论

2.1 土壤水分反演模型

本文使用黑河、温尼伯实验区各自获取的6期VV极化时序Sentinel-1数据（T1、T2、T3、T4、T5、T6），分别基于原始Alpha模型及改进的Alpha模型构建观测方程组，结合实测数据严格设定α系数边界进行土壤水分反演，并利用相应时间的站点观测数据对结果进行验证。图1给出了两种方法反演的结果散点图对比（所有站点所有时相的数据），其中横轴为实测土壤水分（%），纵轴为模型反演结果（%），左边的散点图为原始模型的反演结果，右边为相应的改进后模型的反演结果，明显改进后模型的反演结果更靠近Y=X直线，即结果更接近真实值。

为定量评定基于时序Sentinel-1数据的改进Alpha模型的土壤水分反演精度，分别计算了反演结果与实测土壤水分之间的相关系数r和均方根误差RMSE。由图1可知，对于黑河实验区，整体上土壤水分偏低（2%～16%），基于原始方法得到的土壤水分结果与实测值的相关系数为0.473(P＞0.05)，相关性不明显（排除一个异常点，其反演得到的结果为复数）；而在考虑入射角的变化之后，相关系数提高至0.851(P＜0.01)，均方根误差也由0.053减小至0.023，结果更靠近Y=X线。对于温尼伯实验区，与黑河获取的相同时间范围的影像进行土壤水分反演，相对于黑河实验区该区域的土壤更加湿润，且变化范围更大（9%～44%）。通过原始Alpha模型所得的土壤水分结果与真实值之间的相关系数r=0.601(P＜0.01)，表现出一定的相关性，但明显有部分观测点的反演结果偏高，远离回归直线；而通过改进的Alpha模型反演得到的结果如上图所示，原来离散的点均被收聚至回归线附近，更靠近Y=X线，相关系数由0.601提高至0.821(P＜0.01)，RMSE则由0.152降低至0.065。综合两个实验区的所有站点数据如图2所示，模型改进后得到的土壤水分与实测数据间的相关性由0.720提高至0.893，RMSE由0.138减小至0.059，改进后Alpha模型得到的结果优于原始模型。

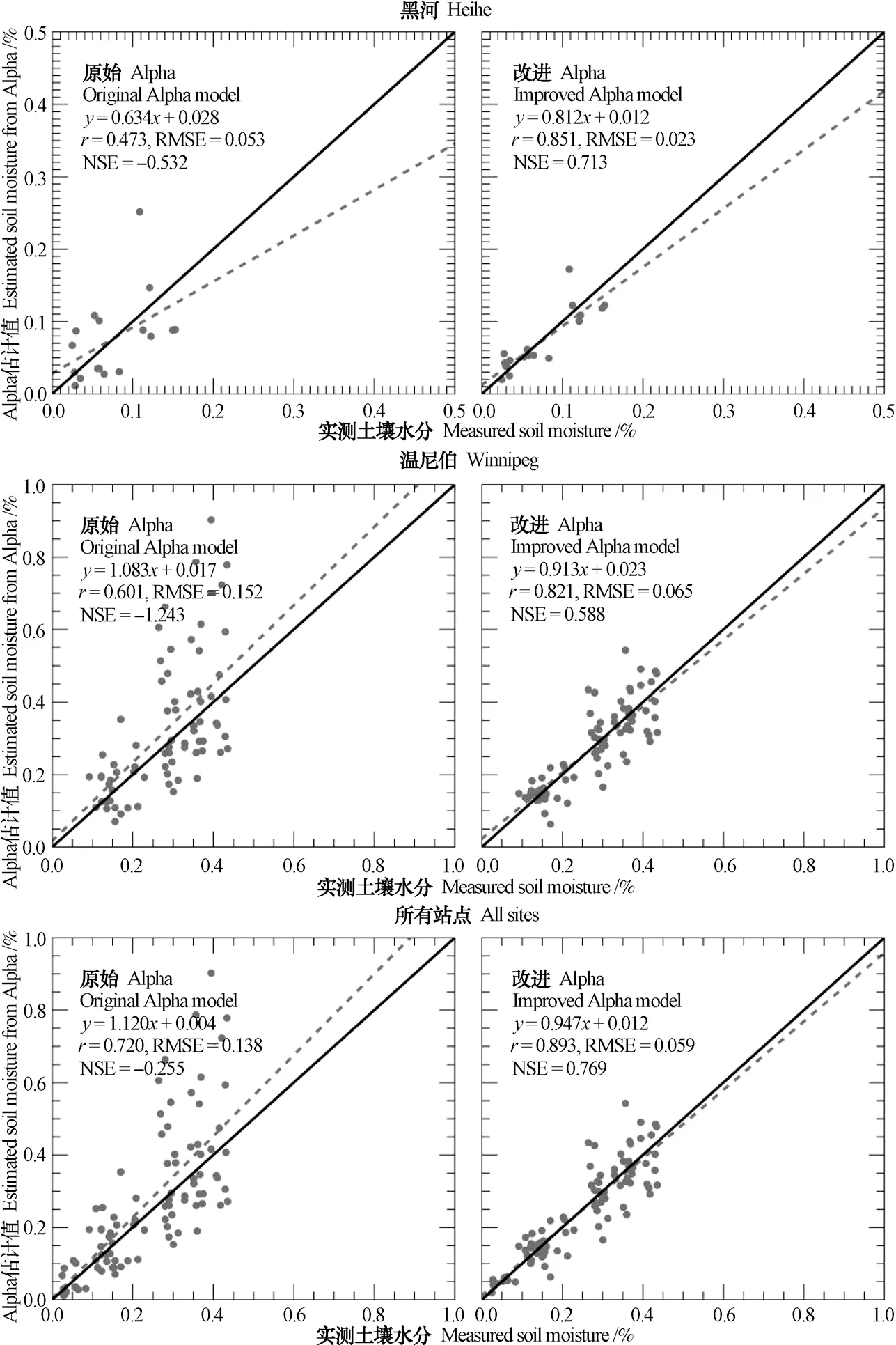
图1 实验区土壤水分反演结果散点图Fig.1 Scatter graph of the inversion of soil moisture in the experimental areas

为进一步评价模型质量本文引入了水文领域中常用的模型评价指标纳什效率系数NSE(Nash Sutcliffe efficiency coefficient)，该系数一般用以验证水文模型模拟结果的好坏，也可用于其他模型。其计算公式如下：

2.2 单站点反演精度

为进一步说明改进Alpha模型土壤水分反演结果，分别在两个实验区选择单个站点的反演结果进行对比分析。如图3所示，横轴代表观测日期，纵轴代表土壤水分，方框实线代表实测土壤水分，空心圆虚线代表原始模型的反演结果，实心圆虚线代表改进模型的反演结果。由图可知，两个站点使用改进后模型的反演结果相较于原始方法更接近于实测情况。对于黑河实验区的大满站点，其2016-11-24的土壤水分相较于前一时期是减小的，但是原始模型得到的结果呈上升趋势，由影像的入射角信息可知（表1），在该时期中大满站点的入射角约为33°，较之前一时期减少了近10°，根据Ulaby等［35］的研究，在超过某一角度临界值后，随着观测的入射角增大雷达接收的后向散射信号呈减小趋势，由此推断该时期虽然土壤水分降低使得后向散射系数减小，但由于入射角的减小使得后向散射系数显著增高。本文使用cos4θ这一乘性因子将入射角对地物散射信号的影响考虑进来，使得反演结果捕捉到这一变化趋势。对于2016-12-14的反演结果，其发生的角度变化同上述一致，该时期得到的结果并没有捕捉到土壤水分减小趋势，其可能原因是粗糙度变化造成的，但是相较于原始方法本文的方法仍在一定程度上减小了反演误差。对于温尼伯实验区，入射角是在41°和32°之间交替变化的，因此原始方法得出的结果也呈高低交替的变化趋势，应用改进后模型得到的结果相比于原始模型能较好地还原土壤水分变化的趋势,且误差也明显减小。

2.3 单时期反演精度

图3 单个站点土壤水分反演结果Fig.3 Inversion of soil moisture of a single site

以上从单个站点时间序列角度对反演结果进行了对比分析，接下来本文将从空间角度对反演的土壤水分进行分析与讨论。表2列出了温尼伯实验区使用原始和改进的Alpha模型反演得到的各时期土壤水分结果精度对比，由表可知无论是原始模型还是改进后模型其结果的相关性均很显著，相关系数r均大于0.8，改进后模型的反演结果相关性略有提高，r均在0.9以上。这是由于温尼伯实验区各个站点的南北纵向分布，使得卫星过境扫描时站土壤水分点间的入射角差异较小，最大角度差不超过3°，因此，雷达观测的后向散射系数与土壤水分之间呈较好的相关性，受入射角影响较小。但是从回归直线的斜率以及均方根误差RMSE的角度来评价反演结果，原始模型则在整体上表现出较差的适用性，而改进后Alpha模型的反演结果则有明显提高，回归直线斜率更加接近于1，即更接近实测土壤水分值；RMSE(m3∙m-3)变化范围由原来的0.043～0.290减小至0.034～0.10。综上所述，本文提出的改进Alpha近似模型可以很好地校正由于时序SAR数据入射角变化带来的土壤水分反演结果误差。

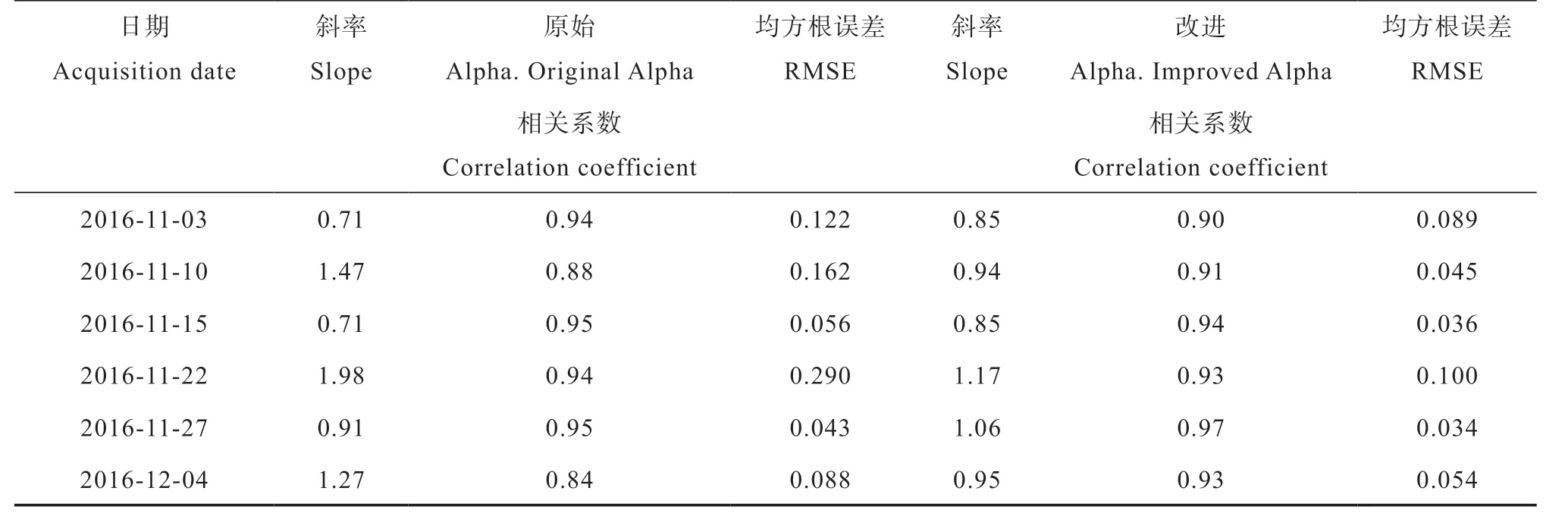
表2 温尼伯实验区各时期反演结果精度对比Table 2 Comparison of inversions of soil moisture in the Winnipeg experimental area in accuracy relative to time

值得注意的是，当入射角发生变化时不仅影响地物的后向散射，也会影响地表粗糙度的响应模式，即在不同入射角下粗糙度对后向散射信号的影响存在差异，因此利用本文的改进模型并不能完全消除入射角变化带来的影响，粗糙度的影响仍存在其中。此外通过卫星观测得到的是像元范围内的土壤水分的整体情况，而站点观测得到的是单个点的信息，土壤水分的空间异质性及测量过程的不确定性使得这种尺度转换存在误差，从而影响算法的结果验证，上述问题均需要进一步的研究和分析。

3 结 论

基于Alpha模型，使用C波段的雷达数据进行土壤水分反演，不同时相数据不同的入射角影响结果的反演精度甚至使得模型不可用，通过本文提出的方法可以很好地校正角度变化带来的影响，扩展了Alpha模型的应用。改进的Alpha模型是在小扰动模型SPM基础上推导得到的，小扰动模型只适用局限的表面粗糙度范围，通过本文实验表明该模型在农田区域具有较好的适用性。

本文研究存在一些不足，实验中使用Sentinel-1 C 波段雷达数据在农田区域进行模型验证，未考虑在其他地表类型（如草地）及其他波段（如L、X波段）雷达数据的适用性，此外需要进一步探讨改进后Alpha模型在高分三号卫星中的应用，其空间分辨率可达1 m，对于中小尺度的土壤水分反演研究具有重要意义。本研究也未考虑植被对于后向散射信号的影响，今后研究可结合相关的植被覆盖区域的微波散射模型及光学影像对Alpha模型进行改进。