吊具夹持机构的结构优化研究
2019-11-16代春香孟令宽李三雁
代春香 孟令宽 李三雁

摘要:为使吊具夹持机构满足载重工况的同时又尽可能降低自身质量及体积,对其进行接触应力、结构强度及优化设计分析,并根据最优设计参数作为制作夹持机构实物的具体数据,以实现对大直径、高质量、高温度零件的吊装。首先,该文采用Ansys Workbench建立夹持机构的参数化有限元模型,并进行接触分析,得出强度相对薄弱位置,进而提出改进和优化方案。其次,建立夹持机构的结构优化模型,采用零阶优化方法进行优化处理,从而得到模型的最优设计参数。从优化结果可得,夹持机构的比重较轻,夹持臂厚度变薄,而此时的最大综合位移和最大等效应力依然满足设计要求。最后,以优化分析结果作为夹持机构的实物制作数据支撑,制作调试后的吊具现场使用状况良好,效果比较理想,可验证分析结果的准确性。
关键词:夹持机构;有限元模型;接触分析;零阶优化方法;结构优化
中图分类号:TH21 文献标志码:A 文章编号:1674-5124(2019)10-0164-05
收稿日期:2018-12-14;收到修改稿日期:2019-02-03
作者简介:代春香(1986-),女,四川遂宁市人,讲师,硕士,研究方向为机械设计、机械电子工程。
通信作者:孟令宽(1987-),男,山东菏泽市人,硕士,研究方向为机械设计与制造。
0 引言
在国民经济建设、国防、航空航天和军工业等诸多领域内较为常见的重要机械设备,多采用多个空心结构体层层嵌套组成的嵌套式伸缩结构[1-2],在降低成本、提高生产效率、实现机械自动化等方面起着积极推动的作用。大型工程机械的结构零件因需要承担较大的载荷和抗弯能力,蔡宇子[3]通过对多种形状截面的受力分析,得出不同的截面形状可使伸缩臂在抗弯和抗扭等方面表现出不同的特点。王中要等[4]利用大型有限元分析软件Ansys对固支梁受集中载荷工况时进行有限元分析,得出工字形截面梁比矩形截面梁的强度和刚度更好的结论。为防止承重件拉伸变形而失衡,在设计机械臂各个截面时,需要考虑多种因素,以使机械手更安全、稳定的工作[5]。结合工作环境及工况,樊炳辉等[6]对管外行走机器人的进行优化分析,设计出满足夹紧力及刚度强度要求的抱紧机构。单雪[7]通过弹塑性力学理论对嵌块齿嵌入海洋基桩机理、嵌块齿间海洋基桩重力分布和嵌块齿受力应力分布情况进行理论分析。
为了实现大直径、高质量、高温度零件的吊装,本文对某吊装机械夹持机构进行了优化分析,该吊具的结构图如图1所示,主要由吊具座、吊臂、夹持臂、夹持驱动机构及纵向调整驱动机构等组成。该机构具有可夹持工件质量大,起吊平稳,可在高温环境下作业,还可提高生产效率等优点。由于要求该机构吊装平稳高效可靠工作,因此,对其进行接触分析并对结构进行优化是很有必要的,通过优化分析,可以获得更合理、更安全的机械参数。
本文根据吊具的初步设计参数,以其中的夹持机构为研究对象。借助Ansys Workbench软件的参数化语言,建立该机构的参数化有限元模型,分析该机构的接触强度;建立其优化模型,采用零阶优化方法进行求解,得到最优设计参数,并以此为依据重新设计制作夹持机构并应用于工程实践。
1 夹持机构接触有限元分析
1.1 夹持机构的有限元模型
夹持机构的等效三维模型如图2所示,其结构上分为吊臂和夹持臂,夹持臂通过电机驱动沿导向槽在吊臂上滑动以实现纵向夹持间距的调整。
本文应用弹塑性增量理论[8]的非線性有限元法来计算吊臂与夹持臂接触面区域的应力,假设弹性变形和塑性变形之间没有耦合的情况。根据增量本构关系的形式和简单加载定理,应力和应变之间可写成全量关系,由弹性应变率和塑性应变率推导出模型方程可由应变分解关系、平衡方程、几何方程和本构关系等组成。
1)分解关系
其中εijel为弹性应变,εijpl为塑性应变,εij(i,j=1,2,3)表示点在正交坐标3个方向的应变分量。
2)平衡方程
σij,i+Fi=0(2)
其中σij,i为应力率场,Fi为体力率。
3)几何方程
其中:εij为应变率场,ui,j、uj,i为运行速度场。
4)本构关系
其中sij为偏应力张量,σ/epl为应力应变曲线数据,eijpl为偏塑性应变张量,σij为应力分量,v为泊松比,E为弹性模量。
在Ansys中建立夹持机构的三维模型,并对吊臂和夹持臂接触面进行如下设置:材料弹性模量E=2.06×1011Pa,密度ρ=7.8×103kg/m3,泊松比v=0.3,以及相关的滑动摩擦系数f=0.13。设置后的模型如图3所示,水平方向深色的吊臂和竖起方向浅灰色夹持臂相接触并在工作中会相互移动,吊臂和夹持臂相对滑动的表面分别是设定为接触面和被接触面。
采用SOLID45三维实体单元对该模型划分有限元网格,共122245个单元,31560个节点,所施加的边界条件共有A~E5个。具体字母参数及其编号所在位置见图4,其中,A:夹持臂夹持工件时所受夹持反力2000N;B:重力加速度9806.6mm·s-2:C:由工件重力所施加的远程力12500N;D:吊臂接口处的对称约束;E:吊臂工字型梁处的固定约束。
1.2 模型的接触分析
很早学者们就开始重视接触问题的研究,瓦伦丁[9]在Hertz研究的弹性体接触问题和相关接触理论的基础上,深入研究了接触力学与摩擦学的相关原理及其应用。颜尚君[10]通过对大功率结构件的接触状态有限元分析并进行应力计算,赵怀璧[11]运用元模型设计方法建立关键零部件的模型,进行受力分析和有限元方法分析。
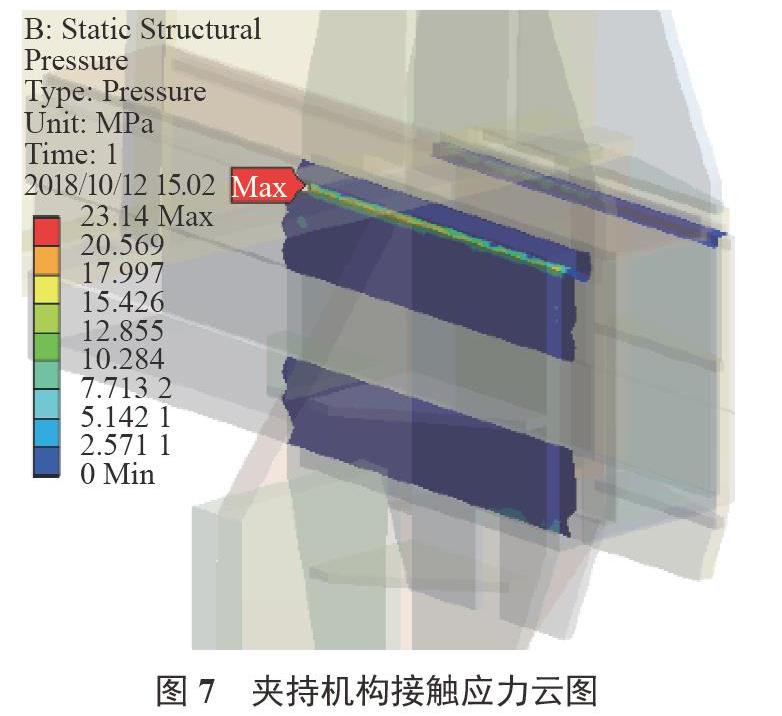
本文采用有限元法在Ansys Workbench中进行面一面非线性接触应力分析,得到计算工况下夹持机构的综合位移云图、等效应力云图和接触应力云图,分别如图5~图7所示。
根据图中结果可知,该机构的最大变形位置在夹持臂底端,值为8.425mm;最大等效应力位于吊臂和夹持臂连接处,值为117.67MPa,其强度相对比较薄弱;接触行为中伴随较高的应力集中,最大接触应力位于相对滑动槽处,值为23.14MPa。由于该机构最大应力出现在吊臂和夹持臂连接处,根据工程实践经验,可以采用添加筋板的方式进行局部加强,且可以针对夹持机构各结构参数进行进一步优化,以达到轻量化的目的。
2 夹持机构结构优化分析
2.1 结构改进措施
根据夹持机构运动范围及对应位置的相关状态,对其标准工况下的综合位移、等效应力和总质量进行优化分析。
首先,设置夹持机构关键部分的结构参数为设计变量,可知其综合位移x主要是关于设计变量如夹持臂厚度、连接座立板厚度、连接板厚度和补充筋板厚度的方程:
x=(j_h,ll_h,l_h,bj_h)(6)
设计变量的初始值及取值范围如表1所示。
其次,為保证夹持机构的刚度与强度要求,取其最大综合位移和最大等效应力为状态变量[12].
ymax(x)≤y0,σmax(x)≤σ0(7)
式中:y0——初始设计时机构的最大综合位移;
σ0——初始设计时机构的最大等效应力;
ymax(x)每次迭代的最大综合位移;
σmax(x)每次迭代的最大等效应力。
最后,取夹持机构总体积为优化目标,从而实现夹持机构总质量的优化,目标函数为
f(x)=Usum(x)(8)
其中Vsum(x)为优化过程中每次迭代的总体积。
因此,夹持机构结构优化的数学模型可表达为
y(x)≤y0
σ(x)≤σ0
minf(x)
2.2 优化前后数据对比
为了对关键部件进行参数优化设计,王奎洋等[13]运用Ansys软件对叶片进行强度分析和模态分析,杨瑞峰等[14]通过结构优化与有限元分析,运用零阶优化算法对其弹性杆进行优化设计。现根据结构优化的数学模型,建立夹持机构的优化设计模型,采用零阶优化方法对该结构进行优化分析。当求解程序迭代至第11步时收敛,图8所示为目标函数的迭代曲线,图9所示为状态变量的迭代曲线。
优化后此夹持机构的最优设计参数如表2所示。由表可知,机构的关键零件的厚度都有所降低,夹持臂厚度降低了20%,连接座立板厚度降低了17%,连接板厚度降低了10%,补充筋板厚度降低了50%。
2.3 优化结果分析
结构优化后,夹持机构的实际质量为766.6kg,相对优化前减轻了12.5%,其中夹持臂厚度由50mm优化至40mm,优化后最大综合位移和最大等效应力依然满足设计要求,可见优化效果良好。
3 优化后的夹持机构
以分析和优化结果作为吊具机构结构设计的依据,并修正夹持机构的结构设计参数,进行设备制作,制作完成后的夹持机构实物如图10所示。该吊具已在某热处理行业中投入使用,对经过高温加热或者带腐蚀的大尺寸坯料进行搬运,实现了普通吊夹具无法完成的工况,且吊装现场使用效果良好,未见机械强度刚度方面异常问题,验证了分析结果的准确性。
4 结束语
为了高效吊装大直径、高质量、高温度的圆柱形工件,对所设计的夹持机构进行接触分析及结构优化分析;在Ansys软件中建立了夹持机构参数化有限元模型,并对初始设计参数下的机构进行接触有限元分析,得出机构相对薄弱位置和进一步的改进优化方案。为实现夹持机构的轻量化目的,建立了夹持系统的优化模型,并采用零阶优化方法进行求解。结果表明,在结构强度满足设计要求的情况下,优化后机构的质量减轻了12.5%;根据优化求解得到的最优设计参数,重新设计并制作了夹持机构,并付诸使用,使用可靠且情况良好。
参考文献
[1]薛盼.汽车起重机臂架结构分析与优化设计研究[D].兰州:兰州理工大学, 2011.
[2]程鹏.汽车起重机伸缩臂有限元分析及优化设计研究[D].太原:太原科技大学,2012.
[3]蔡宇子.现代伸缩臂截面及尺寸优化研究[D].大连:大连理工大学,2012.
[4]王中要,郭秀文.基于ANSYS的梁结构有限元分析[J].公路,2009(7):159-161.
[5]高微,杨中平,赵荣飞,等.机械手臂结构优化设计[J].机械设计与制造,2006(1):13-15.
[6]樊炳辉,付秀强,高圣志,等.管外行走机器人抱紧机构的优化设计[J].机械设计与制造,2018(11):146-149.
[7]单雪.海洋基桩翻转夹具夹持机理分析与装置研究[D].哈尔滨:哈尔滨工程大学,2017.
[8]王仁,黄文彬.塑性力学引论(修订版)[M].北京:北京大学出版社,1992:130-142.
[9]瓦伦丁,L.波波夫.接触力学与摩擦学的原理及其应用[M].李强,雒建斌,译.北京:北京大学出版社,2011:41-52.
[10]颜尚君,李录平,周曙明,等.大功率汽轮机末级轮盘-叶片结构接触状态有限元分析[J].汽轮机技术,2018,60(3):185-188.
[11]赵怀璧.夹钳式钢坯吊具的优化及集成设计研究[D].北京:华北电力大学,2012.
[12]孟令宽,陈晓渝,钱烽,等.液压纠偏机构强度分析及结构优化[J].机械研究与应用,2014,134(27):113-115.
[13]王奎洋,陈炯,唐金花.车用液力缓速器关键部件设计与有限元分析[J].中国测试,2014,40(6):141-144.
[14]杨瑞峰,刘志凯,郭晨霞,等.负载模拟器弹性杆的结构优化与有限元分析[J].中国测试,2016,42(5):119-123.
(编辑:商丹丹)
