基于自适应滤波的薄层厚度超声测量方法

黄巧盛 周世圆 张翰明 姚鹏娇 程垄

摘要：针对应用超声脉冲回波法测量三层结构中的硅橡胶薄层厚度时回波混叠的问题，提出一种基于RLS（recursive least square）自适应滤波的解决方法。该方法将硅橡胶层下界面回波发生混叠的信号作为输入信号，将无硅橡层时的回波信号作为期望信号，通过RLS自适应滤波算法的处理提取出相互分离的有效下界面回波信号，实现硅橡胶薄层的测厚。研究不同滤波器阶数和遗忘因子对信号分离及测厚精度的影响，以输出信号的信噪比为指标选择最优的滤波参数。结果表明：该方法能够有效分离出发生混叠的硅橡胶薄层界下界面回波，能够测量0.15，0.17，0.19，0.21mm4种厚度的硅橡胶薄层，对回波部分混叠和完全混叠两种情况均有良好的适用性。

关键词：薄层测厚;混叠信号分离;自适应滤波;RLS算法;超声脉冲回波法

中图分类号：TB553 文献标志码：A 文章编号：1674-5124（2019）10-0034-06

收稿日期：2019-02-28;收到修改稿日期：2019-03-29

作者简介：黄巧盛（1993-），男，广西钦州市人，硕士研究生，专业方向为超声无损检测。

0 引言

超声波测量具有非接触、非介入、设备简单和精度高的优点，因而广泛用于测距和测厚[1-2]。应用超声脉冲回波法测厚时，由于超声波在薄层上界面的回波的持续时间较长，超声波在薄层中往复传播的时间较短，从而导致上下界面的回波发生混叠，无法直接读取上下界面的回波声时实现测厚。针对这一问题，国内外的学者做了大量的研究：Haines和Bell[3]研究了通过声波垂直入射到多层材料内的声压反射系数幅度谱测量薄层的厚度。李喜孟[4]通过小波变换模极大值法测量了铝表面环氧树脂薄层的厚度，该方法具有较强的噪声适应性。陈秀明[5]分析了超声干涉法的信号变化规律，总结了声压反射系数谱极值的选取原则，提高了该方法的工程应用价值。张伟等[6]基于声压发射系数幅度谱，采用相关系数法对薄层的厚度和声速进行了双参数反演，测量了雷达吸波涂层的厚度。

上述研究主要针对涂层厚度测量，薄层位于基底上，超声波经由耦合剂直接入射到薄层中。对于三层结构中间的硅橡胶薄层，由于上层材料的不均匀性和粘接界面的非理想边界条件的客观存在，检测时的回波信号十分复杂，需要采取合适的处理方法分离出界面回波信号。为此本文提出了基于RLS自适应滤波的信号分离方法，首先分析三层结构中超声波的传播过程，然后选取合适的滤波器阶数和遗忘因子后对信号进行自适应滤波处理提取界面回波，最后通过实验验证该方法合理有效。

1 RLS自适应滤波薄层测厚原理

1.1 三层结构超声波传播过程

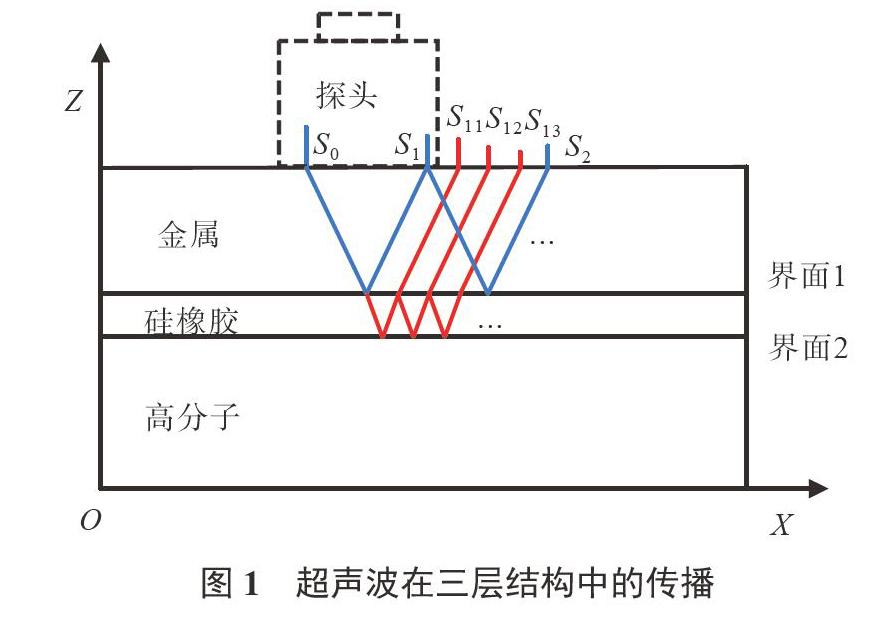
金属一硅橡胶一高分子是典型的三层结构，广泛应用于工业领域。超声波在三层结构中的传播如图1所示，通过耦合剂的耦合，探头发射的激励波S₀垂直入射到三层材料内部，在各层材料的交界面发生折射和反射，形成一个具有多个回波的复杂时域波形信号。由于金属层和硅橡胶薄层的声阻抗差异較大，入射到界面1处的超声波的反射波能量较强，只有小部分能量的透射波进入到硅橡胶层继续传播。界面1处的反射波继续在金属上表面和界面1之间来回反射，在时域上出现界面1的一次回波S₁、二次回波S₂。硅橡胶层的声衰减系数很大，但硅橡胶层一般较薄，因此超声波能在界面1、2间发生多次发射，探头有可能接受到S1回波之后界面2反射的多次回波S₁₁、S₁₂、S₁₃等。高分子材料层的声衰减系数同样很大，超声波穿过界面2传播一段距离后即衰减消失，没有回波信号。

综上所述，理想情况下三层结构的回波信号如图2所示，回波信号之间的时间间隔足够，回波幅值较大，可以直接测得S₁和S₁₁（或S₁₁、S₁₂、S₁₃中的任意两个）的时间差△t，通过公式d=△t×c₂/2（c₂为硅橡胶声速）计算硅橡胶薄层厚度。但在实际情况中，由于S₁的持续时间较长，△t很小，S₁和S₁₁将会重叠在一起，硅橡胶的声衰减系数很大，S₁₂和S₁₃幅值一般很小难以分辨，需要通过一定的方法将S₁和S₁₁分离才能实现硅橡胶薄层测厚。

1.2 RLS自适应滤波原理

自适应滤波是在维纳滤波和卡尔曼滤波等线性滤波器的基础上发展起来的一种最佳滤波器，具有更强的适应性和更优的滤波器性能。自适应滤波器不需要输入信号的先验知识，而是通过前一时刻的滤波器参数计算现时刻的滤波器参数，因而能够适应统计特性未知的噪声。

基于递推最小二乘（RLS）算法的自适应滤波器的递推准则是使加权累计误差代价函数取得最小值，给定n-1次迭代滤波器抽头权向量最小二乘估计，根据新到达的数据计算n次迭代权向量的最新估计[7]。RLS自适应滤波器的递推过程计算复杂，但收敛速度快，且其收敛性能与输入信号的频谱特性无关[8]。

待最小化的代价函数记为ε（n），于是有：其中e（i）是期望信号d（i）与i时刻的横向滤波器输出y（i）之差。即

e（i）=d（i）-y（i）（2）

λ是一个范围为0～1的正数，称为遗忘因子。显然距离当前时刻n越远的过去数据，其权重越小，这使得滤波器能够工作在非平稳环境下。

滤波器输出y（i）由下式计算：

y（i）=w^H（n）u（i）（3）其中u（i）是i时刻抽头的输入向量，

u（i）=[u（i），u（i-1），…，u（i-M+1）]^T（4）

w（n）是i时刻的抽头权向量，

w（n）=[w₀（n），w₁（n），…，w_M-1（n）]^T（5）

M为滤波器阶数。

为了使代价函数取得最小值，求代价函数对权向量的导数并使其为零可得到如下正则方程：

z（n）=r（n）w（n）（6）其中r（n）是自相关矩阵：

z（n）是互相关向量：

由式（6）可知要求得w（n）的最佳估计值，首先要求得自相关矩阵r（n）的逆。由于矩阵求逆运算量非常大，在实际应用中是通过递推法计算权矢量的值191令p（n）=r^-1（n），则RLS算法的递推过程为如下：

1）计算第n个增益矢量

2）计算先验估计误差

e（n）=d（n）-w^H（n-1）u（n）（10）

3）计算权矢量

w（n）=w（n-1）+k（n）e（n）（11）

4）计算自相关矩阵的逆

p（n）=λ^-1（p（n-1）-k（n）u^H（n）p（n-1））（12）

RLS自适应滤波中的滤波器的权矢量随误差信号e（n）的变化而变化，以适应下一时刻的输入信号u（n+ 1），使输出信号y（n+1）接近于期望信号d（n+1），其原理如图3所示。

2 硅橡胶薄层测厚实验

2.1 实验对象和实验系统

本文选取铝一硅橡胶一高分子三层结构作为实验对象，铝、硅橡胶和高分子材料的材料特性参数见表1。

实验系统采用自主搭建的超声脉冲回波检测系统，该实验系统由示波器、超声收发仪和超声波探头组成。示波器采用Tektronix公司的DPO4104示波器，采样频率为5 GS/s，带宽为1GHz。超声波探头选用普通接触式纵波探头，探头中心频率为5MHz。

2.2 硅橡胶测厚实验及分析

2.2.1 测厚信号自适应滤波

铝板和高分子材料之间没有硅橡胶薄层时，示波器采集到的信号如图4所示。从图中可以看出，使用5MHz的纵波探头进行检测时，界面1一次回波S₁的持续时间接近0.5μs，信号的衰减部分持续到1μs。

当硅橡胶层厚度较大时，示波器采集到的信号如图5所示。界面1一次回波S₁和界面2的一次回波S₁₁互相分离，直接测量声时即可实现测厚。

当硅橡胶薄层厚度很薄时，示波器采集到的信号如图6所示。时域信号中没有明显的界面2回波信号，与无硅橡胶层和硅橡胶层厚度较大时的信号相比，S₁回波的持续时间显著增加，可以判断是S₁和S₁₁发生混叠所致。

为了将混叠的回波信号分离，应用RLS自适应滤波算法处理回波信号，将图6所示的混叠信号作为输入信號，图4所示的无硅橡胶层的回波信号作为期望信号。选取滤波器的阶数M二10，遗忘因子λ=0.9，RLS算法初始化如下：w（0）=0;P（0）=δ^-1I，式中δ为正则化参数。正则化参数影响RLS算法的收敛性，应根据信噪比选取，高信噪比时选取小值，低信噪比时选择大值[10]。为保证算法的收敛性，取δ=10。RLS自适应滤波结果如图7所示，S₁回波基本被滤除，只留下少量残余信号，不影响界面2的回波信号的识别。混叠的界面2回波S₁₁和S₁₂被分离出来，测量S₁₁和S₁₂之间的时间差△t，根据公式d=△t×c₂/2计算得到硅橡胶层的厚度。从图7中可以看到，输出信号中存在一定的高频噪声，S₁₁的波峰处发生震荡，通过峰峰值测量△t时会降低测量精度，使硅橡胶层测厚的误差增大。这是由于进行RLS自适应滤波时，滤波器阶数和遗忘因子的值是凭经验选取的，若要得到最优的分离回波信号，需要以输出信号的信噪比为标准选择最优的滤波器阶数和遗忘因子。

2.2.2 滤波器阶数和遗忘因子的选择

RLS自适应滤波器的阶数M影响滤波器输出信号的误差和信噪比。若滤波器的阶数太低，则稳态均方误差明显增加，输出信号将引入由于滤波器权向量与最优权向量失配引起的噪声;若滤波器的阶数太高，则会使自适应算法的计算量变得非常大[11]。遗忘因子λ影响自适应算法的收敛速度和跟踪性能，其值越小，则对时变参数的跟踪能力越强，但同时对噪声越敏感;其值越大，则跟踪能力减弱，但对噪声不敏感，收敛时的参数估计误差也越小[12]。

对如图6所示的0.15mm硅橡胶混叠信号进行RLS自适应滤波，M=5，λ取不同值时的滤波结果如图8所示。可以看到，λ=0.8时信号自适应滤波结果最好，分离出的信号幅值大，高频噪声小。λ=0.9时输出信号的幅值变小，且存在一定的高频噪声，波峰波谷处发生震荡。λ=0.99时输出信号的幅值最小，且存在严重的高频噪声。测量各信号的S₁₁和S₁₂之间的时间差△t，根据表1中的硅橡胶声速计算得到硅橡胶的厚度，如表2所示。可以发现，M=5，λ大于0.8时，随着遗忘因子的增大，输出信号的高频噪声增大，测厚的误差也随之增大。

为了实现最优滤波，把输出信号的信噪比作为衡量指标，选取合适的滤波器阶数M和遗忘因子λ。对输出信号作傅里叶变换得到频谱图，根据频谱图计算信噪比。M=5，λ=0.9时的频谱图如图9所示，由频谱图可知回波信号的能量集中在5MHz附近，与所用探头的中心频率一致，在高频段和低频段存在一定的噪声。由于无法准确得知噪声和回波信号的能量，用式（13）的信噪比代替传统的信噪比定义[13]：式中D_S为回波信号的频段，D_N为噪声信号的频段。

滤波器阶数M和遗忘因子λ与输出信号的信噪比的关系如图10所示。可以看出，遗忘因子不变时，输出信号的信噪比随滤波器阶数的增大先变大后变小再缓慢增加。遗忘因子取小于0.9的值时，变化趋势一致，最大值在滤波器阶数取5时取得。当遗忘因子等于0.9时，滤波器的信噪比在7阶以后随滤波器阶数增大而增加，但仍小于其他遗忘因子的信噪比。滤波器的阶数一定时随遗忘因子的增大，信噪比先增大后减小，在λ=0.8时取得最大值。当滤波器的阶数等于5，遗忘因子λ=0.8时，输出信号具有最大的信噪比。

2.2.3 测厚结果及分析

通过前面的分析可知，对混叠的硅橡胶层信号进行自适应滤波时，应取滤波器的阶数M=5，遗忘因子λ=0.8。取4种不同厚度的硅橡胶层的回波信号，混叠信号及其自适应滤波结果如图11～图18所示。RLS自适应滤波后，时域上出现界面2的两个回波信号S₁₁和S₁₂。0.15mm和0.17mm厚的信號中S₁₁和S₁₂都发生混叠，0.19mm和0.21mm厚的信号中S₁₂回波实际并未发生混叠，但从混叠信号上无法确定S₁₂是界面2的第几次回波，因此这种情况下RLS自适应滤波仍有使用的必要性。硅橡胶层厚度越小，S₁₁和S₁₂之间的界限越不清晰，0.15mm厚的硅橡胶的S₁₁和S₁₂回波已经十分接近，因此小于0.15mm的硅橡胶层测厚需要调整超声检测参数以取得更短的脉冲持续时间。

在自适应滤波分离出界面2回波信号的基础上，测量S₁₁和S₁₂之间的时间差△t，根据公式d=△t×c₂/2计算得到硅橡胶层的厚度。对不同厚度的硅橡胶层进行10次重复测量，结果如表3和表4所示。从表中可知，由RLS自适应滤波算法分离出的回波信号测量得到的声时△t的标准差小于0.0066μs，测量结果具有良好的重复性，硅橡胶薄层的厚度测量误差在3.5%以内。

3 结束语

本文针对使用超声脉冲回波法测量硅橡胶薄层厚度时回波混叠的问题，提出了一种基于RLS自适应滤波的回波信号分离方法，实现了三层结构中硅橡胶薄层的混叠回波信号分离。在介绍RLS自适应滤波信号处理方法的基础上，本文对无硅橡胶、厚硅橡胶层和薄硅橡胶层的信号进行了对比分析，基于输出信号的信噪比研究了不同滤波器阶数和遗忘因子对测厚精度的影响，通过选择信噪比最优的滤波器参数成功测量了0.15mm、0.17mm、0.19mm和0.21mm4种硅橡胶层的厚度，从而验证了该方法对部分混叠和完全混叠的回波信号进行混叠回波分离测厚的可行性。

参考文献

[1]MAEV R G，SHAD H，MAEVA E Y.Thickness measurementof a curved multilayered polymer system by using anultrasonic pulseecho method[J].Materials Characterization，1998，41（2-3）：97-105.

[2]MULLER H，SC'HALLER N，EVER T.Ultrasonicdetenxiinaion of thickness of masticatory mucosa：amethodologic study[J].Oral Surgery，Oral Medicine，OralPathology，Oral Radiology and Endodontology，1999，88（2）：248-253.

[3]HAINES N F，BELL J C，MCLNLYRE P J.The application ofbroadband ultrasonic spectroscopy to the study of layeredmedia[J].The Journal of the Acoustical Society of America，1978，65（6）：1645-1651.

[4]李喜孟，林莉，聂颖.薄层结构超声信号的小波分析[J].无损探伤，2006，30（4）：53-56.

[5]陈秀明，林莉，李喜孟，等.超声干涉法薄层厚度测量声阻抗匹配判据及其应用[J].航空材料学报，2009，29（1）：87-91.

[6]张伟，马志远，赫丽华，等.基于声压反射系数幅度谱匹配分析的薄层厚度和超声纵波声速双参数反演[J].材料工程，2016，44（10）：74-79.

[7]马国栋，阎树田，贺成柱，等.基于LMS算法与RLS算法自适应滤波及仿真分析[J].电子设计工程，2014，22（6）：43-49.

[8]西蒙赫金.自适应滤波器原理[M].北京：电子工业出版社，2003：344-347.

[9]龚耀寰.自适应滤波-时域自适应滤波和智能天线[M].北京：电子工业出版社，2003：92-95.

[10]刘梅，金龙.基于自适应RLS算法的系统辨识应用[J].中山大学研究生学刊，2013，34（1）：80-89.

[11]林川，冯全源.应用于自适应格型RLS滤波器的变阶数算法[J].信号处理，2010，26（2）：298-302.

[12]陈涵，刘会金，李大路，等.可变遗忘因子递推最小二乘法对时变参数测量[J].高电压技术，2008，34（7）：1474-1477.

[13]柳建楠，刘文峰，王伯雄，等.应用于超声测距的小波变换滤波算法[J].清华大学学报（自然科学版），2012，52（7）：951-955.

（编辑：刘杨）