BP神经网络数字识别的Matlab实现

文/罗莉

1 引言

BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络，已广泛应用于模式识别、函数逼近、信号处理和自动控制等领域，是目前应用最广泛的神经网络。

在目前数学和工程计算领域较为通用的软件Matlab中，针对神经网络系统的分析与设计，提供了大量可供直接调用的工具箱函数、图形用户界面和Simulink仿真工具，是进行神经网络系统分析与设计的一个很好的工具。

在使用Matlab建模BP神经网络过程中，需要调用函数newff建立一个可训练的前馈网络，此函数存在新旧两个版本，而现在文献介绍的都是旧版本的使用，对于新版本如何使用却鲜有介绍。导致现在很多用户使用新版本训练函数newff时，遇到训练结果不理想的问题，苦于找不到原因。本文即以数字识别为例，一方面指出新老版本newff使用上的区别，另一方面对常见的训练函数进行对比实验，找到了适用于本文案例的最佳训练函数。

2 基于数字识别的BP神经网络构建

现需要设计一个三层BP神经网络对数字0至9进行分类识别，训练数据如图1所示，测试数据如图2所示，文献[5]中有描述。

该分类问题有10类，由此可设计出BP网络的输出层有10个结点，可采用如图3所示的输出目标矩阵。

图3中的第1列向量代表数字0的目标输出，第2列向量代表数字1的目标输出，第3列向量代表数字2的目标输出，以此类推……

由图1可知训练数据的每个数字可用9×7的网格表示，用白色像素代表0，灰色像素代表1，可将网格表示为0或者1的长位串。位映射由左上角开始向下直到网格的整个一列，然后重复其他列。如数字“1”的网格的数字串表示为｛0,0,0,0,0,0,0,0,0；0,0,0,0,0,0,0,1,0；0,0,1,0,0,0,0,1,0；0,1,1,1,1,1,1,1,0；0,0,0,0,0,0,0,1,0；0,0,0,0,0,0,0,1,0；0,0,0,0,0,0,0,0,0｝。由此可确定输入层有9×7=63个结点，对应上述网格的映射。

输入与输出层的结点个数已确定，分别是63和10，对于此类比较简单的分类问题，选用一个隐层即可。隐层结点数如何确定？对于BP网络结构中隐层结点数的选取没有完善的理论可以利用，目前均是进行摸索试验。一般地，确定三层BP网络的隐层结点数的经验公式有如下几个：（m为隐层结点数；n为输入层节点数；l为输出层结点数；α为1～10之间的常数）。基于上面3个经验公式，我们又经过多次摸索试验，最终决定隐层结点数设置为20比较优，于是构造出网络结构为63-20-10的BP神经网络，如图4所示。

图1：数字分类训练数据

图2：数字分类测试数据

3 Matlab实现

3.1 newff函数新旧版本区别及实现

使用Matlab创建神经网络时，需要用到newff函数建立网络对象，但若使用旧版本的newff函数，会出现警告信息，这是由于使用了旧版本的newff参数列表。解决方法很简单，就是改为新版本形式的参数列表。旧版本中第一个参数需要结合minmax()函数使用，新版本不需要了；另外新版本中不需要指定输出层的神经元个数，改为由输入参数output决定，其他参数不变。这是新旧版本创建神经网络方法的不同，但存在另外一个问题，即使相同的数据和参数下，新旧版本的计算结果总是不一样，而且二者偏差很大，通常新版本的newff方法的识别率总是偏低。造成此问题的原因是新版本的神经网络函数把训练集分成了3份，即训练集train set,验证集validation set和测试集test set，默认比例为7:1.5:1.5。

而在类似本文案例的BP网络构建中，由于训练数据少，训练集必须要完全保留进行训练，否则训练的效果会出现很大的偏差。通过仔细比较新旧两个子函数，发现新版设置了net.divideFcn属性，其值为'dividerand'，解决办法是在新版net中再添加一条语句：net.divideFcn=''。示例语句如下（其中X是输入向量集，Y是目标输出向量集，数字20是隐层结点数）：

图3：BP网络输出目标值

图4：BP神经网络（63-20-10）结构

上述代码中，X是训练数据（如图1所示），Y是目标输出值（如图3所示），T是测试数据（如图2所示），Sim_T是测试数据识别输出结果。

3.2 训练函数实验比较

确定了BP神经网络的结构以及在Matlab中的实现方法，还需要确定的是训练函数。本文选取了几种常用的训练算法进行实验，有traingd（基本梯度下降法）、traingdm（带有动量项的梯度下降法）、traingdx（带有动量项的自适应学习算法）、trainlm（L-M优化算法）、trainbr（贝叶斯正则法）。

表1：不同训练函数实验结果比较

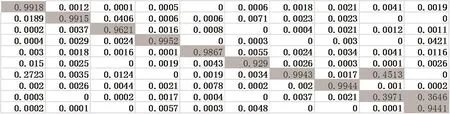
图5：trainbr测试输出结果

设定训练目标（goal）的值为1e-05，最小性能梯度（min_grad）的值为1e-025，学习步长（lr）的值为1，隐层和输出层的传递函数都设置为“tansig”，其它为默认值，可参考文献[8][9][10]。针对本文的要求进行多次实验，下面给出实验结果对照表1。

本文实验所采用的Matlab版本为R2016b，实验电脑CPU配置为Intel Pentium G2030 3.0GHz。

表1中的实验数据是对各种训练函数连续运行20次后取的平均值。

从表1中“测试数据识别成功率”一项可看出，只有trainbr的识别成功率非常高，几乎100%准确，其它几种训练函数的识别成功率都在50%左右，效果不理想。图5 给出了trainbr某一次训练后测试数据识别输出结果，图6为trainbr训练数据均方误差曲线。

由图5可见，trainbr的测试输出结果符合分类识别要求。图2所示测试数据都有一个或者多个位丢失。测试结果表明，除了8以外，所有被测数字都能够被正确地识别。图5数据所示，对于测试数字8，对应数字6的结点上的输出值为0.4513，而对应数字8的结点上的输出值为0.3971，表明第8个测试数据是模糊的，可能是数字6，也可能是数字8。实际上，人识别这个数字时也会发生这种错误；对于测试数字9，丢失的像素点较多，但人眼识别出来还是数字9的可能性最大，测试输出的结果也是符合的，在对应数字9的结点上的输出值为0.9441，而对应数字8的结点上的输出值为0.3646，说明数字8的可能性，但是没有数字9的可能性大。

经过多次试验比对，trainbr最符合本文所述识别训练算法，识别结果高度符合且准确，和其它几种算法相比，虽然多占一些运行内存，但训练收敛时间却是相对比较短的。

4 结论

在Matlab中使用newff函数创建神经网络对象时，对于如本文类似的识别问题（训练数据少），要注意将divideFcn置于空，不对训练集进行划分。通过对多种常见的训练函数进行实验和比较，最后确定了trainbr（贝叶斯规则法）作为本文的数字分类的训练方法效果最优，识别准确率高，另外通过本文实验也验证了trainbr算法的泛化能力强的特点。

图6：trainbr训练数据均方误差曲线