不同安装条件下涡街流量计流场特性的数值仿真研究

摘要：为研究不同管道条件对涡街流量计测量结果及内部流场产生的影响，该文针对2种不同直管段长度时涡街流量计的旋涡脱落频率进行仿真计算与实验测试，结果显示仿真计算与实验测试结果具有较好的一致性，验证数值仿真用于涡街流量计流场分析的可行性。在此基础上，对上下游直管段长度不足、上游有单个90°弯头、下游有单个90°弯头这3种管道条件下共13种不同长度情况对应的涡街流量计的流场特性进行了仿真计算，结果表明，前端直管段长度的减少对测量结果的影响较后直管段更为明显;信号强度与直管段长度没有直接关系;前端有弯头时，频率值大幅降低，最大误差达-60.62%，弯头离旋涡发生体越近，降幅越大;后端有弯头对测量结果影响相对较小，最大误差为-13.23%。

关键词：涡街流量计;管道条件;安装影响;旋涡脱落频率;流场特性;数值仿真

中图分类号：TB937 文献标志码：A 文章编号：1674-5124（2019）05-0110-06

收稿日期：2019-01-30;收到修改稿日期：2019-03-12

作者简介：陈文琳（1988-），女，甘肃武威市人，工程师，博士研究生，研究方向为工程流体力学。

0 引言

涡街流量计自20世纪60年代末开始研制以来，发展非常迅速，可适用于液体、气体、蒸汽，是一种比较先进、理想的流量仪表[1]。但涡街流量计尚属发展中的流量计，其理论基础及实践经验均较为缺乏，所以仍需对涡街流量计做大量的基础研究，避免在实际使用过程中产生一些预料不到的问题。

涡街流量计在使用过程中对所需直管段长度及管壁粗糙度都有一定要求，其校准结果及流量的稳定性取决于上下游直管段的长度以及节流部件的组成，只有满足相应的要求，涡街流量计才能保持相应精度[2]。上游弯头会使管道中产生不对称回旋流，旋涡的存在会影响取压口附近壁面的压力分布，进而影响流量计的计量结果[3]。英国萨里大学和英国国家工程实验室[2]、日本国家计量科学研究院[4]、天津大学的郑丹丹等[5]都分别针对不同安装条件下的涡街流量计测量性能的变化开展了实验研究。实流实验可以得到一定条件下的具体测量结果，但却无法观察到管道内部流场的变化及特性。

用数值仿真方法研究流体流场能够实时直观地观察到流场的变化，对研究流场的具体特性具有很强的指导意义。近年来，不少学者利用计算机仿真对涡街流量计特性进行了大量研究[6-8]。为了准确获取涡流发生器后面涡旋脱落的主要频率，Jian-LinChen[9]进行了一系列数值试验，以确定管道中的各种人口流动条件如何影响特定涡街流量计中涡流发生器下游的主要频率的特征。苏庆文[10]利用计算流体力学数值计算仿真方法，对涡街流量计在不同介质下（空气、蒸汽、水）的流场特性进行分析，发现由于受气体可压缩性等物理特性影响，涡街流量计的流场存在差异，导致测量结果在不同介质条件下存有偏差。彭能[10]利用CFD对大口径管道涡街发生体处的流场特性进行了分析。根据分析得出的结论结合大口径管道发生体的机械特性，提出了位于发生体处基于差压原理的旋涡频率检测方案。宋佳忆[11]则探索了三维流场中涡街流量计的最佳取压位置，得出目前最常用的三角柱旋涡发生体的最佳取压位置位于管道中轴线，距离发生体尾部1.4d处。

本文经实验验证仿真方法的可行性后，利用ANSYSFLUENT流体计算软件对不同上下游（即流量计前后端）直管段长度下涡街流量计的旋涡脱落频率进行了仿真计算，研究不同管道条件对涡街流量计测量结果及内部流场产生的影响，并对相关原因进行了分析。

1 涡街流量计测量原理

涡街流量计利用流体振动原理进行流量测量，在特定的流动条们下，流体一部分动能转化为振动，期辰动频率与流速（流体流量）有确定的比例关系。

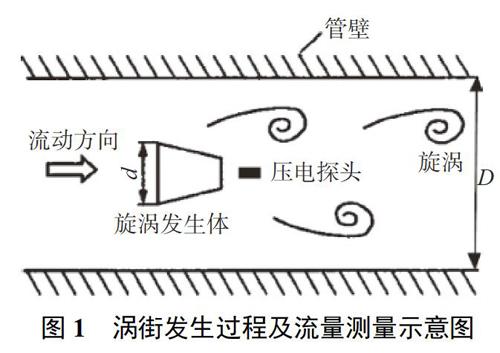
在与被测介质流向垂直的方向放置一非流线型旋涡发生体，当流体流过该旋涡发生体时，在发生体迎流面后方两侧交替分离释放出两列规则的旋涡[12]。涡街发生过程及流量测量过程如图1所示。

管道内流体平均流速v、旋涡脱落频率f关系为

ν=f·m·d/S_t式中：ν——被测流体的流速，m/s;

f——旋涡脱落频率，Hz;

m——旋涡发生体两侧弓形流通面积之和与管道的横截面之比;

d——旋涡发生体的截流面宽度，m;

S_t——斯特劳哈尔数。

在一定雷诺数范围内，S_t可视为常数[13]，涡街流量传感器通过检测旋涡频率f，利用上式来测定流体流速，进而得到流量值。

2 涡街流量计流场仿真

2.1 仿真模型建立与计算条件设定

利用ANSYSICEM建立相应管道的二维几何模型，并划分网格。模型分为前后为直管段、前端有单个90°弯头、后端有单个90°弯头3种管道条件。旋涡发生体的尺寸见图2，设计模拟管道示意图见图3，其中D为管道直径50mm，n为变量，表示不同管道长度。

将ICEM中建好的网格导入FLUENT中进行仿真计算，针对涡街流场为非定常流动，且雷诺数较高等条件，FLUENT中的求解条件设置如下，其余参数保持初始设定：

1）求解器：基于压力的二维双精度瞬态求解器，采用simplec算法;

2）湍流模型：RNG k-ε模型;

3）流体属性：①空气;②密度：1.225kg/m³;③运动粘度：1.7894×10^-5m²/s;

4）邊界条件：①入口：速度入口（根据需要设置不同的流速）;②出口：压力出口（零压）;

5）时间步长：取决于网格大小AX和流速v，T=△X/ν，根据波形再做适当的调整;

6）监测点：监测参数为旋涡发生体后0.7d处的静态压力。

2.2 仿真结果分析

以前后端均为充足直管段长度的仿真模拟结果作为基准数据。调整空气介质人口流速分别为5m/s、10m/s、20m/s、30m/s，取压监测点设在旋涡发生体后0.7d处，运行一定步数后，波形呈现周期性。对于不同的入口速度，管道内旋涡产生、速度场以及压力场的分布情况相似，区别仅在于旋涡脱落频率f及振幅不同，以管道长度为前10D后10D、空气流速为30m/s时计算结果为例来进行分析：图4展示了旋涡发生体后一定周期内的旋涡脱落情况，发生体两侧旋涡依次交替形成和脱落，方向相反，随着流体流动旋涡强度逐渐减弱。

图5展示了监测点处随着旋涡的形成和脱落所产生的静压力分布及演变情况，压力随着旋涡的发生、脱落而随之周期性变化。

图6（a）为相应条件下监测点所承受静压力的变化情况，从图中可以看到该监测点的静压力随着时间呈周期性变化。为了得到与其对应的频率值，对该结果进行傅里叶变换（FFT），从而得到旋涡的脱落频率及对应的信号强度（图6（b））。

3 实验结果与仿真结果的比较

为了与仿真结果进行比较，在新疆计量测试研究院临界流文丘里喷嘴法气体流量标准装置（负压法）上进行了实验，装置信息：U_rel=0.25%（k=2），流量范围为0.1～15000m³/h，是在用的社会公用计量标准。实验设备采用工业中常用的压电式涡街流量计，口径为DN50mm，旋涡发生体尺寸与仿真模拟的尺寸相同，涡街流量计标定精度为1.5级。实验用管道条件取前10D后10D和前5D后10D两种情况，实验条件与仿真定义的条件基本相同。

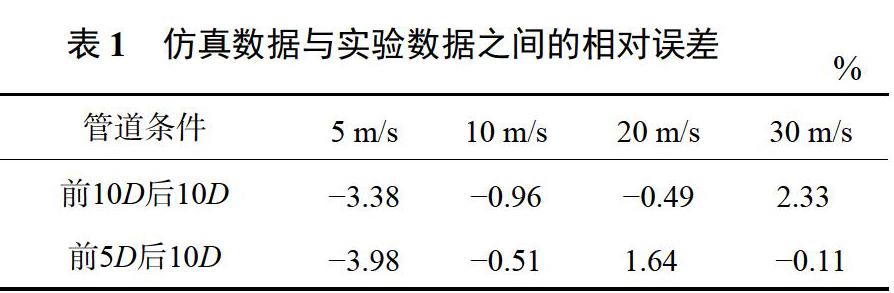
图7、图8所示为仿真结果与实验结果的比较，表1为仿真数据与实验数据间的误差。从仿真数据与实验数据比较的结果来看两者较为接近，最大误差仅为-3.98%，说明应用FLUENT进行流场仿真计算，能够比较真实地反映实际条件下旋涡脱落的频率，仿真结果是可信的，因此将FLUENT数值仿真用于不同安装条件下涡街流量计的流场特性的研究也是可行的。

4 不同管道条件下的仿真结果分析

基于以上可行性分析，对涡街流量计在前后端均为直管段、前端、后端分别有90°弯头时的流场特性进行了研究。

4.1 前后端均为直管段

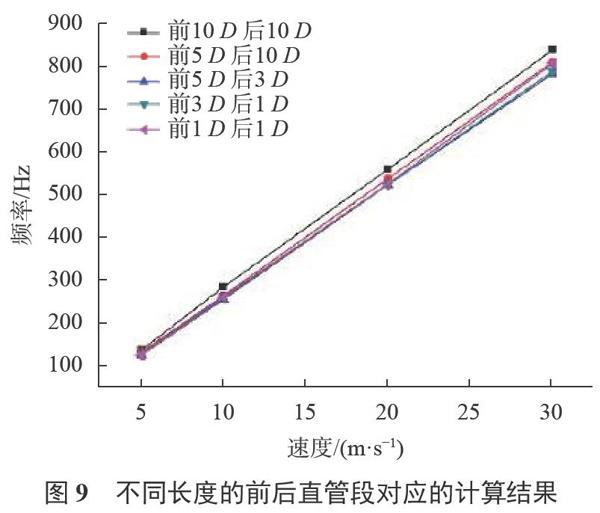
前后端均为直管段的情况分为前10D后10D、前5D后10D、前5D后3D、前3D后1D、前1D后1D共5种情况。具体计算结果见图9。从计算结果可以看出，随着直管段长度的缩短，频率值整体呈下降趋势，并且前端直管段长度的减少对结果影响更为明显。但从图10可以看出，频率信号强度即振幅值与直管段长度没有直接关系。

4.2 前端有90°弯头

前端有90°弯头的情况分别取前端1D、3D、10D、20D、30D、40D处有弯头，后端直管段长度均取5D，以前10D后10D直管段的数据为参考，各管道条件下的计算结果如图11所示。

可以看出，前端有弯头时直管段长度越短，也就是弯头离旋涡发生体越近，得出的频率值即管道内的流量值越小，随着直管段长度增加，频率值逐渐增加，当前端直管段长度增加至40D时，计算结果才与前后直管段充足时的结果接近，也就是说，在实际使用过程中，如果前端有90°弯头，那么前直管段长度不得低于40D。各管道条件下的频率误差见表2。

以前1D弯头后5D直管段的管道条件下、速度为30m/s时的流场情况为例来分析相关流场特性。从流场的压力云图（图12（a））来看，由于弯头的存在使得流体在管壁两侧的压力分布不均，外侧压力增大，内侧压力减小，流速增大时内侧甚至形成空穴;速度矢量图（图12（b））显示了管道内流体整体流动情况，压力较小的地方以及速度较快的部分速度矢量密度都比较大。

速度云图（图13）则充分体现出了管壁两侧压力不均带来的影响：管壁外侧由于压力较高，旋涡脱落的更快，而内侧由于压力较低旋涡脱落较慢，导致发生体两侧旋涡交替脱落的频率减小，即计算结果偏小。

4.3 后端有90°弯头

后端有90°弯头的情况分别取前端10D直管段后端5D有弯头、前端10D直管段后端1D有弯头、前端1D直管段后端5D有弯头、前端1D直管段后端1D有弯头4种情况，同样以前10D后10D直管段的数据为参考，各管道条件下计算结果见图14，频率误差见表3。

从计算结果可以看出，当前直管段长度为10D满足安装要求时，后端有弯头对计算结果影响较小，最大误差仅为4.01%;但当前直管段仅为1D时，后端有弯头的影响更为显著，误差最大扩大到-13.23%，因此在实际使用过程中，如果后端有90°弯头，在前直管段长度充足的条件下，应控制后端直管段长度不低于5D才能在一定程度上保证测量精度。

从速度云图（图15）可以看出，与前端有弯头时的情况恰恰相反，后端有弯头时管道内侧的旋涡脱落频率较快，外侧相对较慢，但整体上也会导致监测点的压力变化频率减慢，即计算结果也会偏低，这与实际情况吻合。

5 结束语

综上所述，本文用实验验证了前后均为直管段时的两种数值仿真计算结果，并对前后均为直管段但长度不足、前端有90°弯头、后端有90°弯头这3种管道条件下对频率值的输出影响进行了研究，得出结论具体如下：

1）仿真结果与实验结果有较好的一致性，表明用数值仿真的方法对涡街流量计流场特性进行分析是可行的;

2）前后直管段不足时，直管段长度越短，输出的频率值越小，对应计算出来的流量就会越小，并且前端直管段長度的减少对结果影响更为明显;同时，输出的频率信号强度即振幅值与直管段长度没有直接关系;

3）当管道前端有90°弯头时，频率值大幅降低，弯头离旋涡发生体越近，降幅越大;当前直管段长度增加值40D时，计算结果才与前后直管段充足时的结果接近;

4）管道后端有90°弯头时，当前直管段长度为10D满足安装要求时，后端有弯头对计算结果影响较小;但当前直管段仅为1D时，后端有弯头的影响更为显著，误差最大扩大到一1323%。

参考文献

[1]邢娟.涡街流量计工况条件适应性研究[D].天津：天津大学，2009.

[2]MOTTRAM R C.Vortex flowmeters-Installationeffects[J].Flow Measurement&Instrumentation，1991，2（1）：56-60.

[3]SINGH R K，SINGH S N，SESHADRI V.CID prediction ofthe effects of the upstream elbow fittings on the performanceof cone flowmeters[J].Flow Measurement andInstrumentation，2010，21（2）：88-97.

[4]TAKAMOTO M，UTSUMI H，WATANABE N，et al.Installation effects on vortex shedding flowmeters[J].FlowMeasurement&Instrumentation，1993，4（4）：277-285.

[5]郑丹丹，唐兴华，张涛.上游单弯头和闸阀对涡街流量计测量性能影响[J].天津大学学报（自然科学与工程技术版），2011，44（12）：1124-1130.

[6]CHEN D S，CUI B L，ZHU Z C.Numerical simulation of theeffect of upstream swirling flow on swirl meterperformance[J].热科学学报（英文版），2018，27（2）：117-124.

[7]FORDC L，WINROTH P H.Vortex-meter design：theinfluence of shedding-body geometry on sheddingcharacteristics[J].Flow Measurement&Instrumentation，2018，59：S0955598617301875.

[8]YAGMUR S，DOGAN S，AKSOY MH，et al.Comparison offlow characteristics around an equilateral triangular cylindervia PIV and Large Eddy Simulation methods[J].FlowMeasurement&Instrumentation，2017，55（6）：23-36.

[9]CHEN J L.Frequency characteristics of a vortex flowmeter invarious inlet velocity profiles[J].Advances in MechanicalEngineering，2017，9（3）：1-6.

[10]彭能，李斌，曹毅杰，等.大口径涡街流量训旋涡频率检测仿真的研究[J].工业控制计算机，2017，30（8）：74-75.

[11]宋佳忆，李斌，陈洁，等.基于CFD的涡街流量计取压位置仿真研究[J].电子测量技术，2015，38（3）：1-4.

[12]VENUGOPAL A，AGRAWAL S V.Review on vortexflowmeter-Designer perspective[J].Sensors and ActuatorsA：Physical，2011，170（1-2）：8-23.

[13]KOGAN E A，SILIN M D.Vortical flowmeter with the use ofthe karman path effect[J].Measurement Techniques，2015，58（6）：1-5.

（編辑：刘杨）