反向钻孔法应用于工件内表面残余应力测量的研究

马小明 欧清扬

摘要：針对现有应力测试难以准确获得工件内壁应力的问题，该文提出于内壁贴片测应变，由外壁钻人的反向钻孔法。应用有限元数值模拟反向钻孔过程，借助生死单元技术获得反向钻孔法测试所需要的应变释放系数a，b;对比反向钻孔法、盲孔法和X射线衍射法对不同厚度钢板的同一测点测得的残余应力结果，以验证反向钻孔法的可行性和可靠度。模拟结果发现，a，b系数与样品壁厚、孔径、剩余钻深均有关系，对此进一步归纳出适用于标准ASTME837中A、B型应变片的a，b系数赋值表。实验结果显示，不同测试方法间虽由于测试范围不同而存在差异，但大部分测试结果保持一致。综合模拟与实验结果，通孔法可以改善原先工件内壁应力测试难的问题，并提高内壁应力的测试精度。

关键词：安全技术;应力测试;盲孔法;有限元数值模拟

中图分类号：TG157 文献标志码：A 文章编号：1674-5124（2019）05-0026-07

收稿日期：2018-05-21;收到修改稿日期：2018-06-21

基金项目：国家科技重大专项（2015ZX06002007）

作者简介：马小明（1962-），男，甘肃天水市人，副教授，硕士，主要从事设备安全检测与失效分析、液化天然气技术等方面的教学、科研等工作。

0 引言

盲孔法测量残余应力由于其较高的精度并且不会对试件造成明显的破坏，在实际生产中广泛应用，以监测工件关键部位的残余应力水平。通过对薄工件（t≤0.4D）钻通孔，或是对厚工件（t≥1.2D）表面钻盲孔，可以获得测点附近的残余应力[1]。但当需要测试厚工件（最常用的1.59mm应变片对应壁厚t≥5mm）内壁的残余应力时，通常只能将试样剖开以暴露内壁，再对内表面钻小孔或采用其他物理法以获得[2]。文献[3]中提到使用机械切割极可能破坏原有应力场并减少可用的测量范围，因此尤其不适用于内壁直径较小而壁厚较大的工件。也可采用全应变释放法测残余应力[4]，但该方法难以避免切削冷却液污染应变片、切割精度低等问题[5-6]。

针对厚壁工件内壁这一测试盲区，本文参考原有对薄工件钻通孔的测试手段，提出在不破坏工件的前提下，于内表面贴应变片，由外壁对应位置钻透内壁测点的反向钻孔法。由于应变片与钻孔方向相对位置的改变，原盲孔法的应变释放系数不再适用于该测法。虽然国内外关于盲孔法的标准[7]中均列有薄板通孔的应变释放系数，但随着工件壁厚增大，该系数是否可用需要进一步确认，因为大部分待测工件都大于薄板的壁厚定义（2mm）。为获得准确的a，b系数，本文使用有限元软件Ansys通过生死单元技术模拟由外壁逐层钻至内壁的过程，并研究不同壁厚、孔径随剩余钻深变化的应变释放规律。

为了更形象地描述该通孔法，图1为通孔法应用的一个实际案例，图中胀管试样内壁内径φ3.5mm，通孔钻深包括管子、管板的壁厚共10.5mm。钻孔法测试的应力区域仅限于2mm的小孔内，尺寸相对管径较小，因此认为胀管曲率不会对应力测试造成过大影响。

1 应变释放系数的计算原理

盲孔法测残余应力的原理即在待测点钻一小孔，用应变片测量钻孔前后周围区域的应变变化，经换算便可表征小孔处的原始应力，如图2所示。弹性力学中有描述带孔平面的应力分布，即Kirsch解析解[8]：

基于忽略沿壁厚方向正应力及剪切力的假设，该平面应力分布可直接用于带孔薄板模型，但对于有一定厚度的三维模型，由于深度方向上的约束，直接应用式（1）会存在误差。式中：d——孔径，mm;

R₁——敏感栅内侧与中心距离，mm;

R₂——敏感栅外侧与中心距离，mm;

E——材料弹性模量，GPa;

μ——泊松比;

σ——孔内材料该方向应力，MPa;

ε——敏感栅测得应变;

θ——孔处平面主应力与应变片方向的夹角，（°）。

虽然无法由解析法直接获得中厚板带孔附近的应力场，但可通过有限元计算或标定试验获得。盲孔法将Kirsch解中各影响因素以应变释放系数a，b代替，再通过对试样的拉伸钻孔，以确定该材料的应变释放系数取值，令：

则式（1）描述为

ε=-1+μ/Ea[σ₁+σ₃）+1/Eb[σ₁-σ₃）cos2θ（2）

式（2）表明盲孔法的应变释放系数在弹性阶段与材料性质基本无关，而与孔径、应变片规格等形状参数有关。另外在许多研究及标准[7]中都阐述了有限元模拟与标定试验结果的一致性，并由模拟总结出应变释放系数与孔深、工件壁厚间的关系。因此，本文也通过三维弹性有限元生死单元技术，对不同壁厚、孔径的模型模拟反向钻孔过程，最终得出随剩余钻深变化的应变释放系数表。具体则在构件中施加已知单向应力场，即将σ₁=σ，σ₃=0代入式（2），由外至内壁去除孔内单元，获得应变片范围内节点沿各自方向上平均的应变变化，即有：

由方向1、3上应变片测得的释放应变ε₁、ε₃和原始施加的双向应力σ₁、σ₃，即可求出应变释放系数a，b。

2 三维弹性有限元分析

考虑钻孔模型的对称性，建立1/4模型通过Ansys进行有限元模拟，分别对孔的两个剖面施加对称约束，对其余两边界面施加全约束。为避免因外力施加于边界处会产生应力集中，使用inistate命令在模型各节点施加了等值均匀的-100MPa初始应力场，采用solid185三维8节点固体结构单元计算。应变片尺寸采用ASTME837-13a中最常用的A型5.13mm应变片，具体尺寸及模型约束如图3所示。

應用生死单元技术模拟反向钻孔过程，如图3右侧所示钻孔方向，以0.1mm每单位时间的“下钻，速度令孔内单元刚度为0。20mm厚的模型钻通孔后，孔边的应力分布如图4所示，图中原始应力为-100MPa，方向沿x轴。可见通孔结果与平面圆孔孔口应力191分布规律十分相似，数值差异原因在于Ansys模型相对平面圆孔模型在厚度上有一定的约束。

在Ansys post26后处理中可查看敏感栅中点在该方向上随钻深变化的应变变化，如图5所示，与后文中a，b应变释放系数随孔深变化的规律相似。将σ₁=σ，σ₃=0代入式（2）得：

可见在均匀应力状态下，敏感栅处随钻深的应变变化是a，b应变释放系数线性运算所得，因此应变变化规律与a，b系数随钻深变化的规律相似。由以上云图及时间历程变量可反映该有限元计算模型的准确性。

2.1 应变释放系数a，b与工件壁厚t的关系

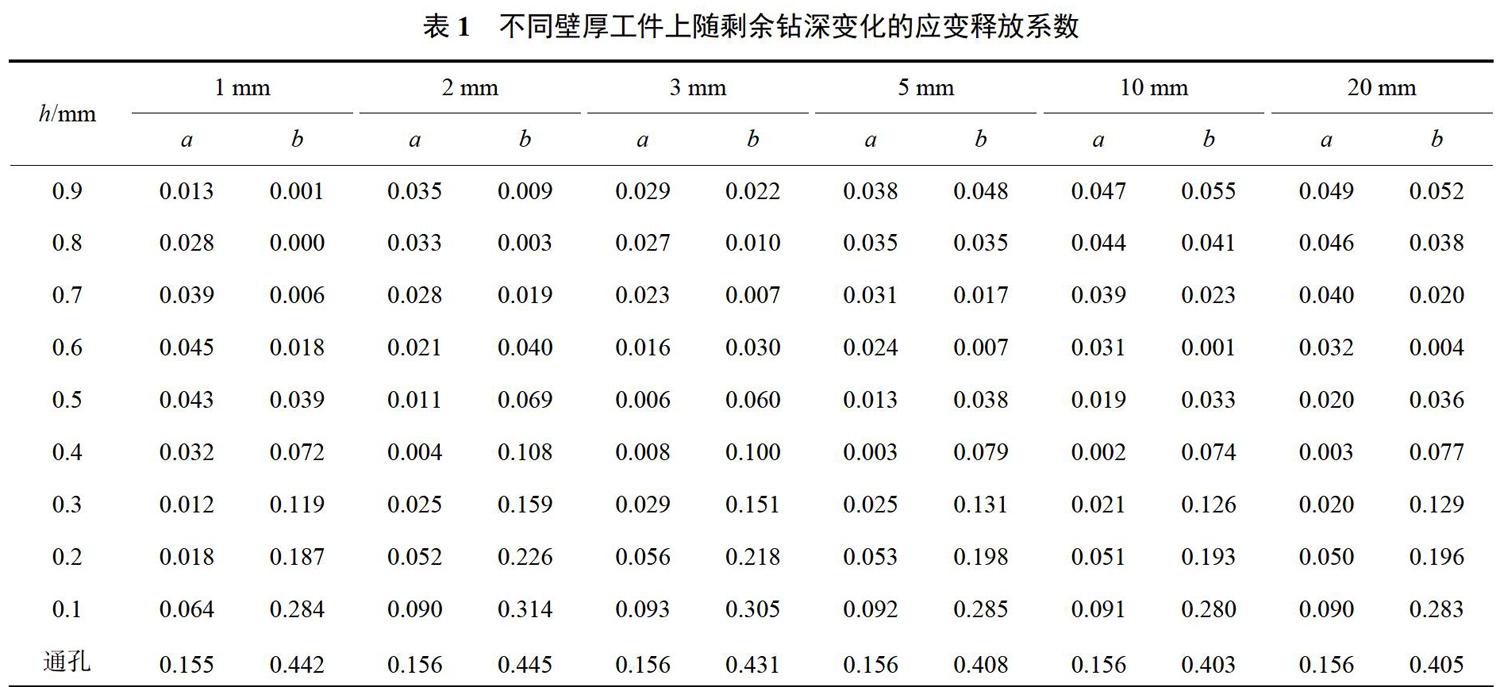
由式（1）算得当孔径为2.03mm时，a=0.157、b=0.463，这与ASTM E837中通孔的应变释放系数一致。而在中厚板上钻通孔的时候，应变释放系数是否随壁厚变化，可通过有限元计算确定。本文建立了6个壁厚范围在1～50mm的模型，覆盖了标准所定义的薄板以及厚板。计算结果见表1，图6显示不同壁厚t的工件其系数a，b随剩余钻深h变化的规律。

由有限元结果发现当载荷在材料弹性范围内时，由外壁钻向内壁直至剩余钻深约0.30.6mm，即h/d（d为孔径）约为0.15～0.3时，内壁开始发生应力释放。随着钻深的增加，内壁表面所测得的应变加速变化。壁厚越薄，内壁开始应力释放的响应越晚，即应变释放系数a，b在剩余钻深更小的时候才开始增长。不同壁厚工件钻通孔的应变释放系数基本与解析结果一致，但当壁厚大于2倍孔径时，由于材料厚度上的约束加深，钻通孔的系数b比解析解小10%。随着壁厚继续增大，应变释放系数a，b基本不再发生变化，不同壁厚工件的释放曲线也非常相似。此结果表明实际通孔法测试内壁应力时可不考虑试样的壁厚，但中厚板（壁厚>2倍孔径）的应变释放系数取值应取小10%。

2.2 应变释放系数a，b与孔径比留刀的关系

图7为载荷σ=100MPa时，随着孔径d的增大，应变释放系数随剩余钻深变化的关系。D为应变片敏感栅中心到孔心的直径，模型中取1/16 in（1 in=2.54cm）A型应变片的尺寸即D=5.13mm，h仍为钻向内壁过程的剩余钻深。

可以看出孔径即使变化，a，b系数随剩余钻深变化的趋势一致，对图7中系数曲线做分段多项式回归分析获得拐点数据如表2所示，发现a，b系数在钻至各个对应拐点后迅速发生应力释放。孔径越小，内壁越早发生应力释放，如d/D为0.3即孔径为1.539mm的模型，在剩余钻深0.6mm时就开始应力释放;而d/D为0.5即孔径2.565mm的模型在剩余钻深小于0.4mm时内壁才开始应力的释放。该结果表示在使用同种应变片钻通孔测内壁应力时，使用越小直径的钻头可获得越多可用的应力释放数据，因为孔径越大钻孔应力释放的速率越快，难以捕捉到将孔钻透前的应变释放。这在图7中也可观察到，孔径越小释放系数a，b增长得越缓慢，意味其内壁的应变释放速率较慢。mm2.3 通孔法内壁应变释放系数a，b赋值表

为了得出类似盲孔法标准中可适用于各种尺寸应变片的应变释放系数，在上文A型1/16in的基础上再建立A型1/32in、1/8in，B型1/16in于孔径比d/D为0.3～0.5的模型。对各模型模拟，系数赋值结果如表3所示。应力开始释放的钻孔深度会随应变片尺寸变化，即表中空白部分表示该钻深下，内壁表面还未产生应变变化。

由外壁钻人内壁时，可先钻至开始应力释放的深度，再以一组钻深增量（0.02D）继续下钻，并记录各钻深增量下的释放应变。并根据表中应变释放系数算出各层平面应力σ_xσ_y，绘制应变一剩余孔深图，若与图6或图7中对应曲线走势非常接近，则表明残余应力沿厚度方向的分布是均匀的。分布均匀的情况下可参考盲孔法标准中对各层应力数据的处理方法，对结果求平均以获得更准确的原始应力。

3 通孔法中应变释放系数的实验验证

由于钻头可切削深度[10]的限制，现只对5块2—13mm厚度，200mm×150mm（长x宽）的45#低碳钢钢板进行应力测试试验，以检验上述应变释放系数a，b的数值计算方法的有效性。45#钢材料参数[11]取弹性模量210GPa，泊松比0.269，钢板命名与具体厚度见表4备注。分别在每块板内表面布置4个测点，测点间距50mm，测点与边界距离超过50mm。

首先使用X-350A型号的X射线应力仪[12]测试4个测点内表面的加工残余应力，测试方法为侧倾固定φ法，2θ扫描范围120°～158°，晶面指数（211），管电压20V管电流5mA，测量平面沿钢板的长边即测得该方向的应力。再于内表面测点贴上BE120-2CA型应变片。通过0.01mm精度的高度尺于钢板的外表面定位各个测点，测点1-3由定位处以0.5mm的钻深进给钻至内表面。钻孔试验使用DH3815N-2静态应变测试系统[13-14]和HK21B型的钻孔装置。测点4使用盲孔法直接测量内表面钻深0.5mm处的残余应力，与X射线法相互验证测试结果。

代入上述数值计算所得不同厚度板材的a，b应变释放系数，算得点1～3反向钻孔法测内壁的应力结果，另外代入ASTM E837中的a，b应变释放系数，算得点4盲孔法测得的应力结果。以上算得沿长边向的应力再与X射线法的应力测试结果相互对比。一共20个测点，每块钢板分别有3组反向钻孔法测内壁和1组盲孔法与X射线法的对比数据。现将误差超过5%的对比组应力结果列表如表4所示。

反向钻孔法与X射线测得的残余应力比较接近，15组中12组的结果差异小于5%。反向钻孔法和X射线测法的影响因素均比较多，但鉴于有一组正常盲孔法与X射线的结果（C4测点）也存在17.4%的误差，笔者分析由于对象材料是轧制钢板，表面加工残余应力大。X射线测量范围为表面几十微米范围内，而盲孔法取了0_5mm深度上的测试数据，两种方法测点位置存在差异，而且材料制造工艺有可能造成钻深上的应力梯度，从而造成了两种方法上的测试误差。

4 結束语

本文针对现有钻孔法难以测得工件内壁表面应力的问题，提出于内壁贴片测应变变化，由外壁向内钻孔，逐层释放应力直至钻通的反向钻孔法。通过有限元分析中厚板孔周应力分布，建立不同型号、孔径、壁厚的应变片模型，基于生死单元技术模拟钻孔过程，获得各个模型随孔深变化的内壁应力释放规律，最终得到可用于该钻孔方式的A、B型应变片应变释放系数a，b赋值表。为了验证数值结果的可靠性，对不同厚度钢板分别使用X射线、盲孔法测试残余应力，与模拟所得应变释放系数计算的应力结果进行对比，实验结果基本与数值模拟结果一致。实际测试中壁厚超过5～的试件很多，在微型钻头不发生挠曲的加工深度范围内，可使用文中算得的厚壁通孔应变释放系数，再结合应变释放系数赋值表可利用未钻透时的应变读数以算得更准确的内壁原始应力。该测试方法可以改善原先工件内壁应力测试难的问题，并提高内壁应力的测试精度。

参考文献

[1]刘一华，贺赟晖，詹春晓，等.盲孔法中释放系数的数值计算方法[J].机械强度，2008，30（1）：33-36.

[2]闫鹏飞.高强铝合金厚板取样切割过程残余应力场演变的研究[D].长沙：中南大学，2010.

[3]C ABRAHAM，GS SCHAJER.Hole-drilling residual stressmeasurement in an intermediate thickness specimen[C]//Proceeding of the 2012 annual conference on experimental andapplied mechanics，2013.

[4]SMITH D J，FARRAHI G H，ZHU W X，et al.Experimentalmeasurement and finite element simulation of the interactionbetween residual stresses and mechanical loading[J].Int JFatigue，2001，23：293-302.

[5]BUCHMANN M，GADOW R，TABELLION J.Experimentaland numerical residual stress analysis of layer coatedcomposites[J].Mater Sci Engng，2000，288（2）：154-159.

[6]YOUNG W，BUDYNAS R，SADEGH A.Roark's Formulasfor stress and strain[M].8th ed.New York：McGraw-Hill，2011：121-158.

[7]Standard test method for determining residual stresses by thehole-drilling strain gage method：ASTM E837-08e2.[S].2013.

[8]李世芸，肖正明.弹性力学及有限元[M].北京：机械工业出版社，2016：75-102.

[9]杨立权，杨立专，吕青青，等.平板孔口应力集中的数值模拟及理论分析[J].煤矿机械，2012，33（2）：65-67.

[10]付连宇，厉学广，郭强.高厚径比微型钻头开发[J].印制电路信息，2010（s1）：440-445.

[11]任建华，付学中，付宇明，等.激光熔覆45钢复合材料力学性能实验[J].塑性工程学报，2012（4）：99-102.

[12]MIYAZAKI T，SASAKI T.A comparison of X-ray stressmeasurement methods based on the fundamental equation[J].Journal of Applied Crystallography，2016，49（2）：426-432.

[13]徐顺飞.静态应变测量的误差分析[J].直升机技术，2010（1）：47-51.

[14]陈惠南.盲孔法测量残余应力A，B系数训算公式讨论[J].机械强度，2009（2）：31-36.