单边核磁共振Halbach磁体结构设计
2019-11-15杜海龙王琦周振宇蒋川东
杜海龙 王琦 周振宇 蒋川东

摘要:传统核磁共振仪器多采用封闭式磁体结构,导致仪器开放性和便携性差,制约其应用范围。为解决上述问题,该文基于电磁场理论,利用二阶有限元方法,研究半环形Halbach磁体的结构设计方法,分析磁块几何结构和尺寸等参数对Halbach磁体产生的中心场强、横向均匀度和纵向梯度的影响。验证该磁体结构无需增加线圈,即可产生核磁共振实验所需的横向均匀纵向梯度分布的磁场。优化后的单边Halbach磁体结构为:磁块尺寸为0.5m×0.095m×0.095m、磁体结构半径为0.63m,在50cm×50cm区域得到中心场强为0.0209T,不均匀度为3.085×10-4,梯度为0.739mT/cm的磁场。
关键词:核磁共振仪器;Halbach磁体;有限元方法;参数优化
中图分类号:TM153 文献标志码:A 文章编号:1674-5124(2019)06-0096-05
收稿日期:2018-10-29;收到修改稿日期:2018-12-03
基金项目:国家自然科学基金资助项目(41604083,41704103)
作者简介:杜海龙(1983-),男,吉林长春市人,工程师,主要从事仪器与检测方法研究。
0 引言
核磁共振作为一种高精度、无损耗的测量技术,广泛应用于地质、医学、生物和化学等领域[1-3]。传统的核磁共振仪器中,多采用封闭式的磁体产生背景磁场,存在体积大、开放性差等问题[4-5]。为了增加其便携性,同时降低仪器成本,国内外学者开展了对单边主磁体结构的研究[6-8]。K.Halbach[9]设计了直线型Halbach磁体结构,但通常用于大型物体检测。Blumich等[10]提出了U型磁体结构,但是U型磁体存在磁场水平方向分布不均匀,导致纵深分辨率差的问题。Chang Weihao等[利用两个尺寸分别为50mmX50mmX50mm和24mmX24mmX5~的永磁体块设计了单边磁体结构,但是该结构产生的磁场在灵敏区域内均匀度和强度均较低。上述单边磁体结构均无法直接产生纵向梯度磁场,需要额外增加梯度线圈。
为实现仅利用磁体即可产生横向均匀、纵向梯度分布的磁场,本文借鉴环形Halbach磁体结构[12],研究了半环形Halbach磁体的原理,分析了磁体剩磁、磁体尺寸结构参数对半环Halbach磁体结构产生的中心场强、磁场均匀度和纵向梯度的影响,最终得到最优的半环Halbach磁体结构的尺寸参数。
1 Halbach磁体设计
1.1 半环型Halbach磁体原理
为了产生横向均匀分布、纵向梯度分布的磁场,本文采用半环Halbach磁体结构,如图1所示。该磁体结构由9个形状、尺寸、剩磁完全相同的磁块组成,箭头为磁化方向。
本文以等效磁荷模型为基础,采用标量磁位法计算Halbach磁体的磁场。根据Maxwell方程组中的高斯定律,可得永磁体产生的空间任意点的标量磁位φ[13-14]为式中:M——滋化强度;
R ——源点到磁场的距离;
ρms——面磁核密度;
Ω——Halbach磁体积分区域;
Γ——磁体边界区域。
为了得到高精度的结果,本文采用二阶有限元方法[15]计算得到标量磁位。首先采用二阶四面体单元对计算区域进行剖分,如图2所示,则每个单元。对应的场为φe。
单元永磁体磁场对应最小泛函问题为其中μe、ρe、σ-e分别为磁导率、体磁荷密度和面磁荷密度。
对式(2)右边求偏导,令其等于零:其中Ni和Nj分别为四面体的主节点和中间节点的插值函数。利用第一类边界条件对式(3)处理后,即得到任意场点处的标量磁位φ,将其代入H=-▽φ中,即可得到单边Halbach磁场强度。
1.2 结构设计
图1中半环型Halbach磁体结构,保持磁体排列为椭圆轨迹服从y2/a2+z2/b2=1(a、b分别为椭圆的长半径和短半径),设计Halbach磁体结构1,磁体的长半径a1=0.55m,磁块的尺寸为0.6m×0.095m×0.095m,剩磁B0=1.5T。经计算,得到灵敏区域内(ROI)为0.5m×0.5m yoz平面磁场如图3所示。可以看出,其中心场强0.04T,左右两边的场强明显大于中间区域,磁场等位线呈上凸趋势,磁场横向均匀度较差,纵向呈梯度分布。因此本文将进一步研究磁块几何结构和磁块尺寸等参数对中心磁场分布的影响。
2 影响因素和参数优化
本节通过研究磁块几何结构和尺寸等参数对Halbach磁體所产生磁场的3个主要参数(中心磁场强度、中心磁场水平方向的均匀度和中心磁场垂直方向的梯度)的影响规律,实现固定ROI区域半环Halbach磁体结构的参数优化设计。
2.1 中心磁场强度
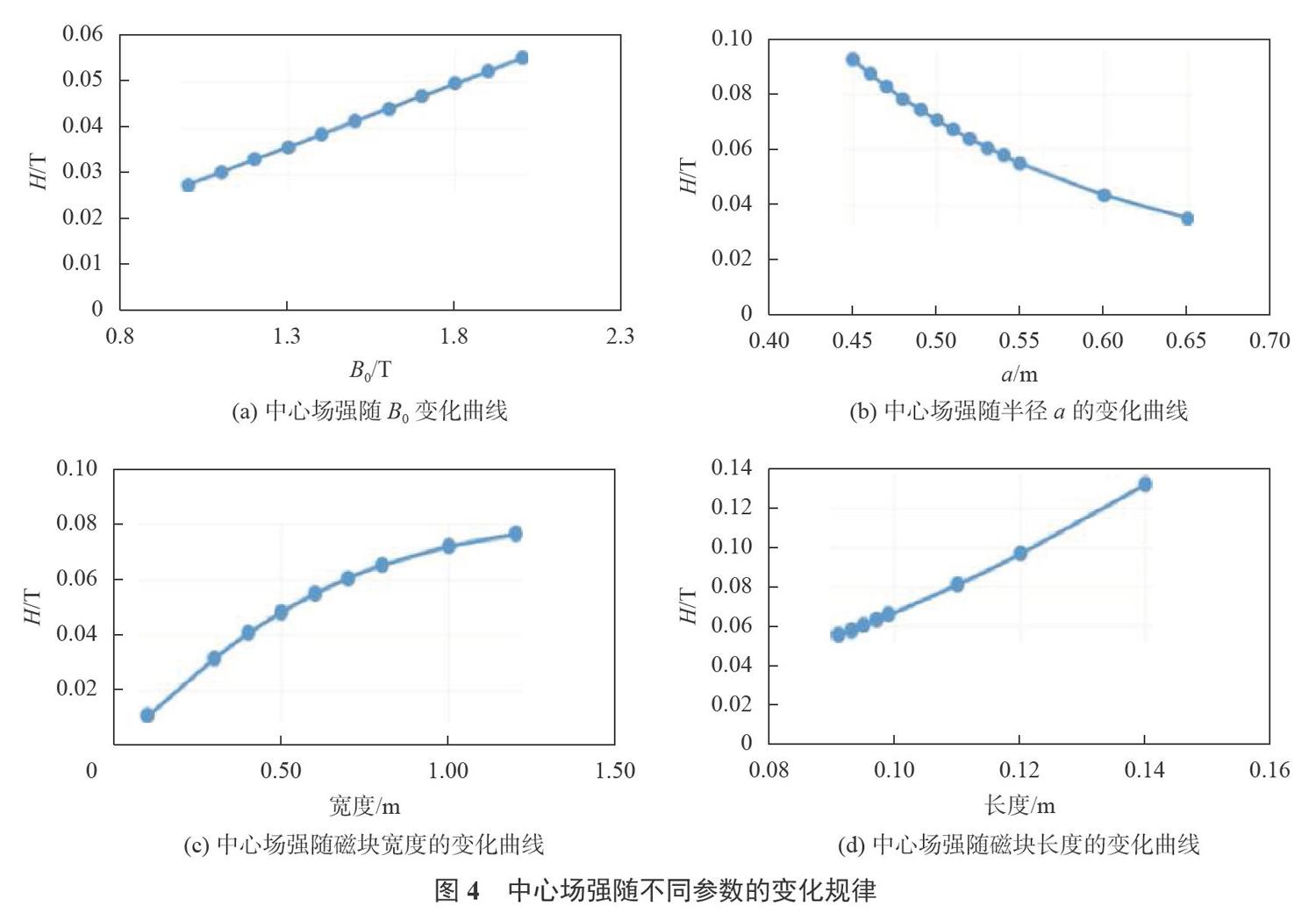
以1.2节中的结构尺寸为例,计算了磁体半径和磁块尺寸不变,不同剩磁Bo对应的中心场强如图4(a)所示。可以看出,中心场强随剩磁的增大而增大,且呈现准线性规律。当B0从1.0T变化至2.0T时,H从0.027 T增大至0.055T。图4(b)给出了中心场强随Halbach磁体结构半径的变化规律,可以看出中心场强随着半径的增大按指数趋势减小。图4(c)和图4(d)给出了剩磁和结构半径保持不变,不同磁块宽度和长度对应的中心场强。可以得出,随着磁块长度和宽度的增加,中心场强均呈现增加规律。
