基于起始触发相位调整的三角波线性度测试方法研究
2019-11-15赵自文秦源淋王阳葛惠君
赵自文 秦源淋 王阳 葛惠君

摘要:为解决信号模拟器专用测试设备三角波线性度的测试标定需求,提出一种基于起始触发相位调整的三角波线性度测试方法。以设备外触发输出作为基准,通过调整三角波的起始触发相位,将三角波的上升沿或下降沿进行梯级水平切割,采用数字示波器和数字电压表组合方式进行监视和测量不同梯级的电压,利用最小二乘法计算出三角波上升沿或下降沿的线性度,并对测量结果的不确定度进行分析评定。测量结果比对表明,设计的三角波线性度测试方法切实可行,能推广应用到函数发生器三角波线性度的测试,具有很好的实用性。
关键词:信号模拟器;三角波;起始触发相位;线性度;测量不确定度
中图分类号:TP395 文献标志码:A 文章编号:1674-5124(2019)06-0024-05
收稿日期:2018-11-15;收到修改稿日期:2018-12-20
基金项目:“十三五”国防技术基础研究项目(JSJL2015205B017)
作者简介:赵自文(1966-),男,河南洛阳市人,研究员,主要从事信号计量保障技术研究及校准设备研制工作。
0 引言
信号模拟器属于导弹产品的专用测试设备,用于测试考核产品的静态性能、动态性能[1],三角波是该类设备产生的一种特征信号,该信号技术参数指标除了频率、幅值有要求外,线性度也有明确指标要求。专用测试设备三角波输出由其内部的信号发生器输出并经二次变换后产生[2],三角波会产生一定程度的失真,因此在产品测试前需对三角波的线性度参数进行测试标定。对于该类设备三角波线性度的测试,若采用数字示波器测量法,数字示波器的电压测量分辨力及测量误差不满足测试要求[3-4]。若按照JJG 840-2015《函数发生器检定规程》[5]中规定的三角波线性度测量方法,使用时存在一定的局限性,1)無法同步观察到三角波的失真状态,不能根据三角波的失真情况及时调整沿上采集点;2)采集三角波的上下峰值点电压非常困难[6];3)对于不同设备不同频率的三角波,由于输出信号与同步信号间存在不同的延迟[7],不易准确设置数字电压表的触发延迟时间;4)该方法计算得到的是三角波上升沿/下降沿10%~90%之间的线性误差,而不是包含峰一峰点在内的线性度。上述两种测试方法均无法直接应用,本文利用设备的触发输出端口而非传统的同步输出端口,结合起始触发相位调整方式,对三角波上升沿/下降沿线性度测试方法进行分析研究。
1 测试方法设计
1.1 专用测试设备三角波参数指标要求
频率:0.1~20Hz,误差优于0.01%;幅值:1~10Vpp,误差优于1%;对称度:50%;线性度:优于0.5%(峰峰点之间)。
1.2 测试方案
鉴于三角波线性度常规测试方法的局限性,本文设计数字电压表和数字示波器组合测试方案,设计以下解决途径:1)用数字电压表和数字示波器同时监视测量,其中数字示波器主要用于观察三角波的失真情况,便于确定上升/下降沿上的相应测试点位置,用数字电压表测试三角波沿上不同测试点对应的电压;2)舍弃常规的设备同步输出模式,利用专测设备的触发输出去同步数字示波器和数字电压表,利用触发输出作基准[8],通过调整三角波的起始触发相位,精确定位三角波上升沿/下降沿上不同测试点的位置;3)利用数字电压表的触发延迟功能,将触发延迟设置在合适的固定时间即可,对于不同测试点的电压测试,无需变更触发延迟时间,简化了操作设置且能保持较高的电压测量准确度;4)精细调整三角波的起始触发相位,采取逐次逼近比较方式获得三角波的峰峰点电压。
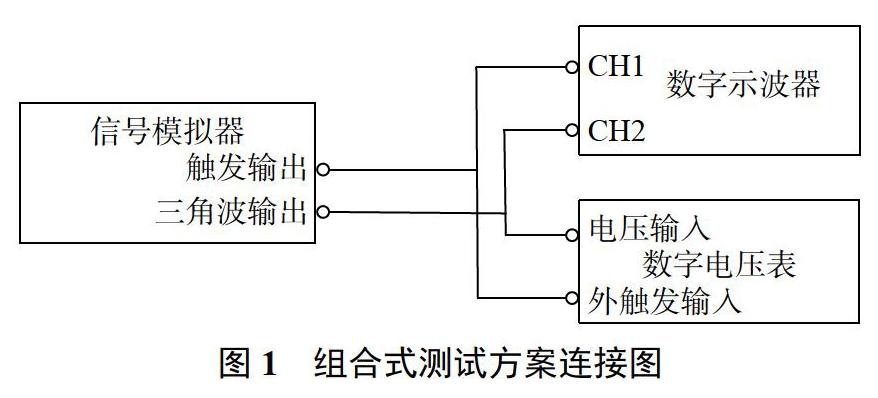
三角波线性度组合测试方案组成如图1所示,该设计方案的关键点是对三角波的起始触发相位进行精密连续调整,等同于对三角波的上升沿/下降沿实施梯级水平切割,如图2和图3所示,最终将三角波沿上位置点xi1的电压测量转换成易测量的梯级水平线上位置点xi2的电压,位置点xi2对应的水平时间范围非常宽,便于数字电压表的准确测量。
测试三角波线性度时,将信号模拟器的触发输出信号连接至数字示波器的CHI通道及数字电压表的外触发输入通道,三角波输出信号连接至数字示波器的CH2通道及数字电压表的电压测量输入通道。信号模拟器的三角波参数设置为:20Hz,1Vpp,零偏置,上升沿触发输出,触发输出单个波形,触发间隔100ms;数字示波器工作在双通道高阻输入模式,垂直带宽限制在20MHz以下,触发源选择为CHI上升沿,垂直灵敏度CHI:1V/div、CH2:0.2V/div,时基5ms/div;数字电压表工作在直流电压测量模式,1V量程,外触发,触发延迟时间适中。
当示波器观察到稳定的三角波显示时,基于波形的失真情况确定起始触发相位的步进间隔,当三角波的上升/下降沿显著失真时需适当减小相位步进间隔,增加三角波沿上测量点数量,信号模拟器最小起始触发相位调整间隔为0.1°。用初始相位-90°作为起始时间t1,记录峰一峰点内不同起始触发相位点θi(对应不同时间点ti)上数字电压表的电压测量结果hi(i=1,2,…,n)。
1.3 测试设备的选用要求
根据三角波参数指标测试需求,采用上述测试方案,选用的数字电压表和数字示波器应满足如下要求:
1)数字电压表
直流电压测量:0~10V,最高分辨力:8位半,误差优于0.02%;具有外触发和触发延迟调整功能。
2)数字示波器
频带宽度:0~100MHz;最高采样率:1GS/s;垂直灵敏度:5mV/div~5V/div,±2%;时基:5ns/div~5s/div,±12×10-5。
1.4 测量结果处理方法
根据三角波上升沿/下降沿不同起始触发相位点θi(对应时间点ti)上的电压测量结果hi,基于最小二乘法计算出最佳拟合直线[9-11]:其中斜率
利用式(1)计算出相应起始相位点θi的最佳拟合值hi',三角波上升沿/下降沿的线性误差为式中:δi——三角波上升/下压降沿线性误差;
hi——三角波上升沿/下降沿起始触发相位第i点的电压测量值,V;
hi'——最佳拟合直线上对应第i点的计算值,V:
A——三角波峰峰电压值,V。
三角波上升沿/下降沿的线性度为
L=max|δi|(3)
2 测量结果及测量不确定度分析评定
2.1 测量结果
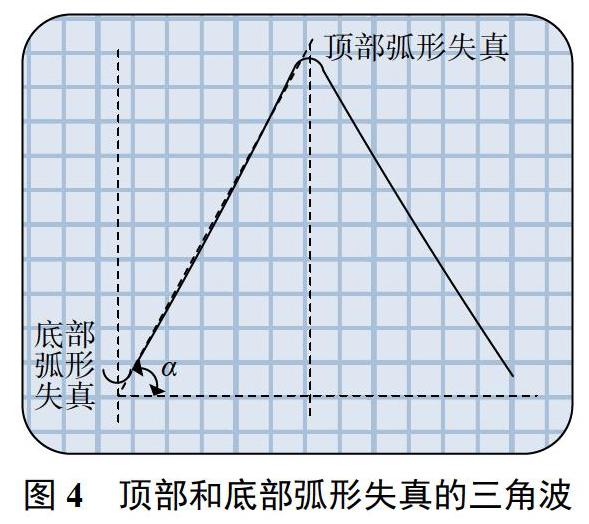
依据上述测试方法对信号模拟器的三角波线性度进行测试,三角波输出信号:20Hz 1 Vpp零偏置。测量用设备:数字电压表3458A,数字示波器MSOX6004A。本文以三角波的上升沿测试为例进行分析,首先用示波器观察三角波波形,波形的波峰和波谷处出现明显的弧形失真,非线性特征明显,为了能兼顾三角波的波峰和波谷点的电压测量,取1.0°作为起始触发相位的步进间隔,在三角波上升沿的波谷和波峰之间-90.0°~90.0°测量181个点,以初始相位-90.0°,点的电压测量结果作为起始值h1,相位90.0°点的电压测量结果作为最末值h181,表1和表2分别是起始触发相位-90.0°—1.0°和0°—90.0°的电压测量结果。
根据表1和表2的电压测量结果,应用最小二乘法求得一元线性回归的最佳拟合直线为:
h'(V)=0.00555025(V/(°))×θ(°)+0.0009144(V)
通过计算测量结果与最佳拟合线对应点之间的残差,判别出-90.0°相位点是最大残差点,其残差为e1=0.002208V。
利用波峰和波谷点电压计算出三角波的峰峰值为A=0.99464Vpp。
则三角波上升沿的线性度L=0.22%。
2.2 测量结果不确定度分析评定
在基于式(2)分析评定三角波线性误差测量不确定度时,可视作有两个自变量,其中分子为观测值hi的残差ei,分母为三角波的峰峰值A,线性误差可由下式表示:
灵敏系数:
1)残差ei引入的标准不确定度u(ei)
最佳拟合直线h'=aθ+b,其斜率a和截距b是通过计算各残差的平方和并使之最小而求得的。
为使E最小,则其对a和b的一阶偏导=0,二阶偏导>0,即:
对以上一阶偏导和二阶偏导求解后,可推导出拟合直线的斜率a和截距b,如式(1)所示。
最佳拟合直线的自由度:v=n-2(其中n为测量点数,2代表上述两个约束条件)[12],若以凡Sh表示观测值hi的方差,则:
残差ei引入的标准不确定度:u(ei)=0.42mV
2)峰峰值A引入的标准不确定度u(A)
三角波顶部和底部出现弧形失真,测量顶部和底部峰值时需要观察波形,通过精细调整三角波的起始触发相位,逐次逼近识别出顶部电压最大值和底部电压最小值。峰峰值A测量时引入的标准不确定度主要来自两个方面,1)三角波的起始触发相位调整分辨力引入的u1(A),2)数字电压表测量误差引入的u2(A),两者均服从均匀分布[13]。
三角波起始触发相位分辨力为0.1°,最佳拟合直线斜率为a=0.00555025 V/(°),如图4所示,在三角波的顶部和底部均按此斜率进行估算。
顶部测量:
同理底部测量:u12(A)=0.16mV
数字电压表在直流1V档的测量误差为:±(1.5×10-6读数+0.3×10-6量程),取测量误差的半宽度,由数字电压表测量误差引入的标准不确定度为:
顶部测量:
同理底部测量:u22(A)=0.61μV
3)合成不确定度及扩展不确定度
U=kuc=0.09%;k=2
线性度:L=0.22%±0.09%
3 测试方法的验证
选用一台Keysight 33220A函数/任意波信号发生器,该台设备由计量机构依据JJG 840-2015《函数发生器检定规程》出具有检定证书,三角波上升沿(10%~90%)最大线性误差为0.06%(1kHz,1Vpp)。
用基于起始触发相位调整的三角波线性度测试方法测试该信号,为了与检定证书的测试点相对应,同样测量10%,20%,…,90%共计9个点,计算出9个点分别对应的起始触发相位,按照本方法测试要求及数据处理方式计算出三角波上升沿(10%~90%)的最大线性误差为0.062%,若测量结果只按一位有效位保留,那么该测量结果与计量机构证书中所给结果完全相同。
4 结束语
采用本文设计的测试方法已对多台信号模拟器的三角波线性度进行了测试,应用效果良好,为型号线提供了一种新的标定测试方法,保证了产品测量结果的准确性。本测试方法设计合理、实用性强,不仅能满足信号模拟器等专用测试设备三角波线性度的标定测试需求,还能推广应用到函数对王意波形发生器三角波线性度的测试。
参考文献
[1]赵自文,徐毓雄,严宜强.空空导弹地面检测设备校准方法研究[J].中国测试,2017,43(12):63-68.
[2]孙晨朔,金祖洋,刘山松.基于Howland电流源产生更优线性度三角波设计[J].电子器件,2014(3):561-564.
[3]吕云朋,孙金伟,张墨一种提高示波器线性度的标定方法[J].现代电子技术,2011(8):204-206.
[4]梁志国,郭洪侠.三角波信号沿线性度的统计分析评价方法[J].航空计测技术,2001(2):3-5.
[5]函数发生器检定规程:JJG840-2015[S].北京:中国质检出版社,2016.
[6]孙艳峰,黄继国,李憬.三角波、锯齿波信号线性度校准技术[J].科技资讯,2015(23):14-16.
[7]钟长胜,王轶尊,高辉.基于CPI」]和DS1020的多通道延迟脉冲发生器[J].电子技术应用,2015(1):57-59.
[8]田林青,李长青.基于DDS信号源外触发功能的多机同步输出解决方案[J].今日电子,2008(4):64-65.
[9]刘庆,邵志新.回归分析的直线拟合不确定度探讨[J].中国测试,2009(3):41-44.
[10]梁志国,孙璟宇.三角波信号波形参数的测量不确定度[J].计测技术,2005(6):57-61.
[11]米娟层.一元线性回归中的不确定度分析[J].煤质技术,2014(1):21-22.
[12]劉渊,丁建华,王茂仁.直线拟合中的不确定度计算[J].物理与工程,2009(2):25-27.
[13]沈才忠,刘志敏,王力敏.不确定度评定在实验室校准方法制定中的应用[J].中国测试技术,2008,34(5):36-38.
(编辑:刘杨)
