γ射线空气比释动能空腔理论计算值准确度的蒙特卡罗研究

滕忠斌 田丽霞 宋明哲 倪宁 张曦 魏可新

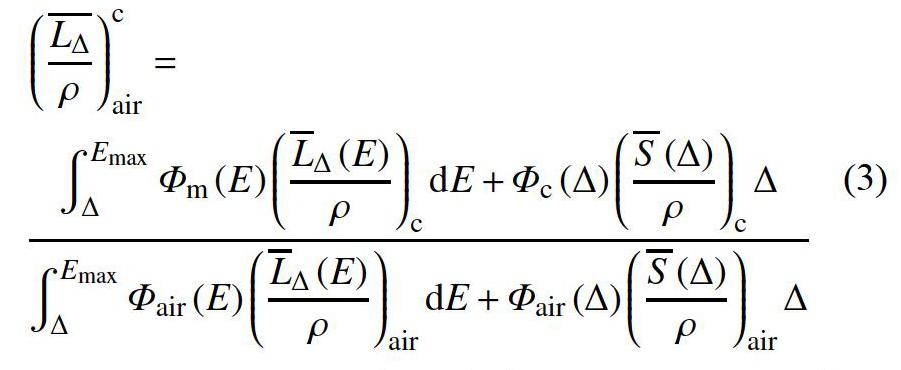
摘要：当使用基于空腔理论的石墨空腔电离室绝对测量γ射线空气比释动能时，需要考虑空腔体积的大小变化对测量结果准确度的影响。利用EGSnrc程序计算得到10～5000cm³的球型石墨空腔电离室的石墨和空气的限制的阻止本领比（L△（E）/ρ）_c，air、入射光子与空腔气体直接作用沉积能量的份额F_air和Spencer-Attix空腔理论修正因子k_SA。结果表明对于⁶⁰Co和¹³⁷Cs能量的光子，在计算（L△（E）/ρ）_c，air时选择合适的A值可以使k_SA的值保持在0.998～1.000之间。此外k_SA的大小随空腔体积的增大有逐渐减小的趋势。表明在设计和使用较大体积（≥50cm³）的石墨空腔电离室时需要考虑合适大小的k_SA值，以保证空腔理论计算值和绝对测量结果的准确。

关键词：空腔理论;限制的阻止本领比;EGSnrc;电离室

中图分类号：TL72 文献标志码：A 文章编号：1674-5124（2019）06-0013-06

收稿日期：2018-09-10;收到修改稿日期：2018-10-15

基金项目：国家自然科学基金（11505028）;核技术应用教育部工程研究中心开放基金资助项目（HJSJYB2015-12）

作者简介：滕忠斌（1993-），男，山东聊城市人，硕士研究生，专业方向为核科学与技术。

通信作者：田丽霞（1983-），女，河北石家庄市人，硕导，博士，研究方向为核技术及应用。

0 引言

为了能够使用空气比释动能标准复现γ射线参考辐射场中的低空气比释动能率，实验室中通常使用替代法进行测量[1]。虽然该方法现实可行，但每次次级标准电离室的校准都会引入测量不确定度。由于基准（或最高标准）电离室对Y射线空气比释动能的绝对测量都是基于空腔理论，如果将电离室的空腔体积增大来得到更低的绝对测量下限从而减少校准次数，那么此时需要考虑空腔体积的变化对空腔理论计算结果准确度的影响。

MA[2]在1991年提出使用光子与空腔气体作用所沉积能量占空腔气体中总沉积能量的份额F_air来判断一个空腔是否可以作为理想条件下的Bragg-Gray空腔。但该因子只是考虑不同条件时的空腔是否可以作为满足空腔理论前提条件的理想空腔，并未说明当该空腔作为实际电离室空腔时是否可以准确测量。Borg[3]和Russa[4]在2000年和2009年先后提出，⁶⁰Co和¹⁹²Ir光子能量和较小的空腔体积时使用Spencer-Attix空腔理论修正因子k_SA或注量扰动因子k_fl来判断空腔理论计算值与真实值之间的差异。引入k_SA的原因是实际空腔的存在打破了Bragg-Gray理论的前提条件[3-5]。k_SA可以用于判断基于Spencer-Attix空腔理论的石墨空腔电离室是否可以准确测量Y射线参考辐射场中某点处的空气比释动能。较小的k_SA值对该点的空气比释动能的准确测量起到了关键作用。

研究目的是探究不同入射光子能量时，空腔电离室体积的变化对空腔理论计算值准确度的影响。使用EGSnrc计算不同光子能量和不同空腔体积时石墨和空气限制的阻止本领比（考虑了不同的密度效应修正和平均激发能推荐值）、必要的修正因子、F_air和k_SA。計算结果可以用于判断较大空腔体积时空腔理论的计算结果是否准确，并且可以用于指导较大石墨空腔电离室（≥50cm³）的制作，最终用于探究γ射线空气比释动能绝对测量下限和减小替代法得到的测量结果测量不确定度。

1 空腔理论

空腔理论可以将介质中的吸收剂量与探测器介质中的吸收剂量联系起来，使得可以用剂量计的读数来评估介质中的吸收剂量。实验室中通常使用基于Bragg-Gray空腔理论的石墨空腔电离室来直接测量γ辐射场中一点的空气比释动能[6]为：式中：Q——空腔内干空气中的电离电荷量;

m_air——参考温度和压力条件下空腔中干空气的质量，m_air=ρ₀V;

ρ₀——参考条件下干空气密度;

V——空腔的体积;

（W/e）_air——在干空气中生成一个离子对，电子所需要消耗的平均能量;

（μ_en/ρ）_air，c——空气与石墨的质能吸收系数之比;

（s/ρ）_c，air石墨和空气的非限制的阻止本领之比：

g_air——次级电子在空气中由于轫致辐射所消耗的能量占初始能量的份额;

——因实际条件与参考条件的差异而对

测量值进行的修正。

由于式（1）使用的是平行光子束，空腔内介质为干空气，所以在∏k_i中排除了空气湿度修正k_h和轴向不均匀性修正k_an，只保留壁效应修正k_wall和Spencer-Attix理论修正k_SA。k_wall可以修正室壁对初级光子的衰减和散射作用，用于重现电离室没有壁情况下空腔内的吸收剂量。k_SA可以用来判断基于Spencer-Attix空腔理论的石墨空腔电离室在绝对测量时是否可以准确测量，也就是说k_SA越接近于1，使用空腔理论计算的结果越准确。k_SA的具体的表达式为：

虽然式（1）使用了非限制的阻止本领比（s/ρ）_c，air，但在国际计量局组织的γ射线空气比释动能国际比对中，各国基准使用的都是限制的阻止本领比[7-8]。那么此时使用的空腔原理亦称之为Spencer-Attix空腔理论。当空腔体积变化时，Spencer-Attix空腔理论较Bragg-Gray空腔理论更适用于空腔内沉积能量的计算。对于能量低于△的电子，认为它们不能穿越空腔，能量就地沉积[9]。在计算石墨中的吸收剂量与空腔气体中的吸收剂量时，针对能量低于△的电子使用了限制的阻止本领，二者之比为：

Spencer-Attix空腔理论与Bragg-Gray空腔理论有两个相同的前提条件：1）空腔足够小，空腔的存在不会改变介质中次级电子的注量和谱分布。2）光子在空腔中的作用可以忽略不计。但在实际γ射线辐射场中空腔内必然存在光子与空腔气体的作用，并且空腔的存在影响了次级电子的注量及其谱分布。当空腔体积逐渐增大时，实际空腔与理想空腔的差异将导致使用式（1）计算的准确度变低。因此在使用较大体积的石墨空腔电离室直接测量空气比释动能时，需要定性和定量地分析式（1）是否准确可靠。

2 方法和结果

2.1 计算模型

EGSnrc是被广泛应用于电离辐射剂量领域中的蒙特卡罗程序，其计算的电离室响应与真实值相差在0.1之内[10]。使用EGSnrc中的用户程序计算式（2）中等号右边所有的物理量和修正因子，计算时的输运选项均使用缺省值。球型石墨空腔電离室被放置在真空中，空腔中充满干空气，石墨壁的厚度为3mm，空腔体积大小在10～5000cm³之间变化。源项设置为0.662MeV和1.25MeV的单能光子以及两种参考辐射场的γ能谱（¹³⁷Cs源加铅衰减后的γ能谱和⁶⁰CO源加铅衰减后的γ能谱，分别记为Cs+Pb能谱和Co+Pb能谱），光子从电离室侧方平行入射，射束直径和室壁外径相等。计算模型如图1。

在计算式（2）物理量和修正因子前，使用EGS_GUI内的用户程序创建计算时需要的PEGS4文件。它包含了计算所需要的材料的种类、密度、截面数据、密度效应修正、平均激发能和截止能量等参数。需要设置的截止能量包括：光子的输运截止能量POUT和产生光子的阈值能量AP，电子输运截止能量ECUT和产生次级电子的阈值能量AE=△+511keV，其中△与电离室的空腔大小有关。对于体积较小的电离室，△通常取值为10keV[5]。它等于电子在干空气中射程为L=4V/A时所对应的能量。L、V和A分别是空腔的平均弦长、体积和表面积。首先需要计算不同空腔体积对应的L值，然后利用电子在干空气中的CSDA射程和电子能量的关系插值得到相应的△值[9]，结果如表I。在PEGS4文件中石墨密度为1.836g·cm^-3，使用ICRU37号报告[11]推荐的平均激发能I_g=78eV，以及石墨在1.7g·cm^-3时的密度效应修正，空气的密度为1.025kg·m^-3。

2.2 光子在空腔中的作用

F_air是初级光子在空腔中沉积的能量占空腔中总沉积能量的份额，它可以用于判断空腔是否满足空腔理论的前提条件。利用CAVSPHnrc分别计算在Cs+Pb能谱、0.662MeV、Co+Pb能潜和1.25MeV4种不同入射光子能量时，不同体积的空腔内光子直接作用沉积的能量DPgas以及相应条件时空腔中总的沉积能量D_gas^total。具体方法为：创建PEGS4文件，其中石墨的截止能量AE大于入射光子能量、ECUT=512keV、AP=POUT=1keV，空气截止能量为AE=ECUT=512keV，AP=POUT=1keV。用CAV SPHnrc计算得到只有光子在空腔中沉积的能量ugaso然后创建新的PEGS4文件，将石墨和空气的截止能量均设置为AE=ECUT=512keV，AP=PCUT=1keV，计算空腔中总的沉积能量D_gas^total，二者之比得到F_air，计算结果如图2，不同入射光子能量，随着空腔体积增加，F_air越来越大。可以得到，空腔体积的增大导致了空腔理论前提条件的失效。这种现象也说明了在式（1）中引入k5A的必要性。

2.3 电离室内吸收剂量D_gas、壁效应修正k_wall和空气比释动能k_air

在用CAV SPHnrc使用计算D_gas时，源项有4种设置，分别是Cs+Pb能谱、单能0.662MeV，Co+Pb能谱和单能1.25MeV。在PEGS4文件中，石墨和空气的截止能量均为AE=ECUT=512keV，AP=PCUT=1keV。通常AE和ECUT越小，模拟计算的结果越准确。但此时计算时间会成倍增加。计算结果如表2。计算时设置光子输运历史数为9×10⁸个，使计算结果的统计不确定度小于0.1%。在计算得到的输出文件中，可以得到相应条件时的壁效应修正因子k_wall。

同样使用CAVSPHnrc计算空腔中的空气比释动能k_air。设置室壁与空腔气体的材料都为空气，室壁的厚度为0_001cm。在计算使用的PEGS4文件中，空气的AE=ECUT=3MeV，AP=PCUT=1keV。此时计算得到的空腔中的吸收剂量就等同于该空腔内的空气比释动能k_air。

2.4 质能吸收系数比（μ_en/ρ）_air，c和g_air

石墨和空气的质能吸收系数（μ_en/ρ）c和（μ_en/ρ）_air以及电子在空气中的辐射能量损失份额gain都可以由g用户程序计算。在计算使用的PEGS4文件中，石墨和空气的截止能量均为AE=ECUT=521keV，AP=PCUT=1keV。设置计算的历史数为10°，计算结果的统计不确定度小于0.1%。

2.5 石墨和空气的限制的阻止本领比（L△（E）/ρ）_c，air

SPRRZnrc是专门用于计算Spencer-Attix限制的阻止本领比的EGSnrc用户程序。在计算时开启光子再生功能，用于消除石墨对初级光子的衰减和散射作用，使石墨内达到带电粒子平衡[12]。在Bethe[11]公式中，材料的平均激发能I和密度效应修正的大小影响了其阻止本领的计算。ICRU37号报告中给出了I_g的推荐值为78eV，而在更新的ICUR90[13]号报告中I_g的推荐值为81eV。因此需要考虑不同I_g值对石墨和空气的限制的阻止本领比的影响。在计算（L△（E）/ρ）_c，air之前，需要创建两个PEGS4文件，一个使用石墨平均激发能I_g=78eV，石墨密度效应修正ρ=1.7g·cm^-3，另一个使用I_g=81eV，密度效应修正ρ=2.265g·cm^-3。此外，△的选择会对阻止本领比的计算值产生影响[14]。利用表1中的△值，设置PEGS4文件中石墨和空气的截止能量均为AE=511keV+△，ECUT=512keV，AP=POUT=512keV，用于（L△（E）/ρ）_c，air的计算，计算结果在表1中。

2.6 Spencer-Attix理论修正因子k_SA

根据上述方法，计算得到式（2）右侧的所有物理量和修正因子，利用式（2）便可以计算出在不同光子入射能量时，各空腔体积大小所对应的kA大小。如图3和图4所示，对于Co+Pb能潜和1.25MeV能量以及Cs+Pb能谱和0.662MeV能量的光子，随着空腔体积的增大，使用AE=511keV+△（△的取值与空腔体积有关，AE用于计算（L△（E）/ρ）_c，air）得到的kA值的比使用AE=521keV（其中A=10keV）得到的ksA值更接近于la这说明对于不同大小的空腔，在計算（L△（E）lρ）_c，air时需要考虑使用合适的△值，而不是仅将△设置为10keV。并且从图3和图4中可以看出，随着空腔体积的增大，k_SA值有逐渐减小的趋势。这说明随着空腔的增大，空腔理论的计算值与真实值的偏差也逐渐增大。因此需要根据合适的kA值以及石墨空腔电离室的实际加工难易程度来确定可以使用的最大空腔体积。

2.7 密度效应修正和平均激发能对k_SA的影响

不同的石墨的密度效应修正和石墨的平均激发能都会影响空腔气体沉积能量的计算结果，从而影响了k_SA的大小。本次研究对比了使用石墨的平均激发能I_g=78eV和石墨体密度效应修正计算的k_SA与石墨的平均激发能I_g=81eV和使用石墨颗粒密度效应修正计算的k_SA。对比结果从表3中可以得到，不同的密度效应修正和平均激发能的选择对k_SA的大小影响很小，相差小于0.1%。

3 结束语

通过上述方法，探究了不同光子能量和不同空腔体积时的球型石墨电离室是否满足空腔理论的前提条件，计算对比了不同条件下γ射线空气比释动能的空腔理论计算值和真实值的差异，即Spencer-Attlx空腔理论修正因子k_SA的大小。且在相同空腔体积和入射光子能量时，本次计算的结果与Borg和Seltzer的计算结果相差小于0.2%。从图2中可以得到：当体积增加时F凡逐渐增大，此时的电离室空腔不能视为理想的Bragg-Gray空腔。但当使用合适的△值来计算（L△（E）/ρ）_c，air时，k_SA的大小可以保持在0.998～1.000之间。从图3和图4中可以得到，对于用于y射线空气比释动能绝对测量的石墨空腔电离室，△取值应该与空腔体积大小有关。并且在设计和使用较大体积的石墨空腔电离室时需要考虑合适的k_SA值大小。从表3中可以得到：不同石墨的密度效应修正和平均激发能对最终k_SA的影响很小，两次计算结果的相对偏差小于0.1%。因此在之后（L△（E）/ρ）_c，air的计算中可以考虑使用ICUR90号报告的I_g和密度效应修正的推荐值。本次研究方法与结果可以为较大体积的石墨空腔电离室在γ射线空气比释动能绝对测量中的设计和使用提供参考。

参考文献

[1]γ射线空气比释动能计量器：JJG 2044-2010[S].北京：中国标准出版社，2011.

[2]MA C M，NAHUM A E.Bragg-Gray theory and ion chamberdosimetry for photon beams[J].Physics in Medicine&Biology，1991，36（4）：413-428.

[3]BORG J，KAWRAKOW I，ROGERS D W，et al.Monte Carlostudy of correction factors for Spencer-Attix cavity theory atphoton energies at or above 100keV[J].Medical Physics，2000，27（8）：1804-1813.

[4]RUSSA D J L，ROGERS D W O.Accuracy of Spencer-Attixcavity theory and calculations of fluence correction factors forthe air kerma formalism[J].Medical Physics，2009，36（9）：4173-4183.

[5]COMMITTEE R T.A protocol for the determination ofabsorbed dose from high-energy photon and electronbeams[J].Medical Physics，1983，10（6）：741-771.

[6]BiJERMANN L，BURNS D T.Air-kerma cavity standards[J].Metrologia，2009，46（2）：24.

[7]ALLISYROBERTS P J，BURNS D T，KESSLER C.Summary of the BIPM.RI（I）-K1 comparison for air kerma in60Co gamma radiation[J].Metrologia，2007，44（1A）：06006.

[8]ALLISYROBERTS P J，KESSLER C，BURNS D T.Summary of the BIPM.RI（I）-K5 comparison for air kerma in137Cs gamma radiation[J].Metrologia，2013，50（1A）：06001.

[9]ATTDt F H.Introduction to Radiological Physics andRadiation Dosimetry[M].New Jersey：John Wiley and Sons，1986.

[10]ROGERS D W O，TREURNIET J.Monte Carlo calculatedwall and axial non-uniformity corrections for primarystandards of air kerma[R].Nrcc Report Pirs，1999.

[11]ICRI.Stopping powers for electrons and positrons[R].ICRUReport No.37.WashingtonDC：ICRI，1984：15-34.

[12]RUSSA L，DANIEL J.The effect of low-energy electrons onthe response of ion chambers to ionizing photon beams[J].ProQuest Dissertations And Theses，2009，71（5）：3119.

[13]ICRU.Key date for ionizing -radiation dosimetry：measurement stands and applications[R].ICRU Report No.90.England：Oxford University Press，2016：15-34.

[14]ROGERS D W，KAWRAKOW I.Monte Carlo calculatedcorrection factors for primary standards of air kerma[J].Medical Physics，2003，30（4）：521-532.

[15]SELTZER S M，JR B P M.Changes in the U.S.primarystandards for the air kerma from gamma-ray beams[J].Journal of Research of the National Institute of Standards&Technology，2003，108（5）：359-381.

（編辑：刘杨）