采用2 b深度像素的弹性运动估计算法

宋传鸣 闵 新 谢维冬 尹宝才 王相海

1(辽宁师范大学计算机与信息技术学院 辽宁大连 116029) 2(大连理工大学计算机科学与技术学院 辽宁大连 116024) 3(东北大学计算机科学与工程学院 沈阳 110169) 4(计算机软件新技术国家重点实验室(南京大学) 南京 210023)

运动估计是一项去除视频冗余的时间域预测技术，为H.264和高效率视频编码(high efficiency video coding, HEVC)等编码标准贡献了大部分的性能提升[1-2].提高运动估计的效率，使其搜索过程更加健壮和高效不仅是视频编码领域的热点问题，也是进一步改善视频编码效率的重要途径之一.

多年来，视频编码标准始终采用了仅能刻画水平、竖直等平移运动的块匹配算法，可是块平移模型既无法有效预测由物体旋转、缩放、变形和摄像机运动产生的非刚性复合运动，又不能准确表示具有复杂形状的运动区域，导致在运动物体边缘产生大幅值的预测残差.并且，随着块尺寸的减小和运动向量精度的提高，用于编码运动向量、块划分方式的码流开销以及各种软硬件资源开销的增加幅度甚至超过了率失真性能的提升幅度[2].故此，研究能有效表示复杂运动场的运动模型及相应的帧间运动估计方法，对下一代视频编码效率的提升具有重要意义[3-6].

鉴于平移运动模型的不足，研究人员将高阶运动模型引入运动估计，利用高阶函数产生1个或多个扭曲的参考帧实现了更高质量的运动补偿.依据模型显式表现形式的不同，本文将这些运动估计补偿算法划分为4类：1)基于网格模型的运动估计[7-9]；2)基于多项式模型的运动估计[10-12]；3)基于缩放模型的运动估计[13-15]；4)基于弹性模型的运动估计[16-20].其中，算法1对编码率失真的优化较为困难[21]；算法2的参数偏多，搜索复杂度高，且对局部运动的刻画能力不足；算法3无法有效描述物体的旋转、错切和局部变形运动；算法4可刻画物体的平移、错切和扭曲运动，既能表示全局和局部运动，又可通过调整模型参数个数来控制运动估计的计算复杂度.因此，对比各类高阶运动模型并综合现有研究结论，弹性运动模型是一种表示复杂运动场的高效模型.

本文首先简要介绍弹性运动估计的相关工作，然后针对其存在的计算量高的问题，引进一种视频帧的2 b深度像素表示方法，进而提出低位深度的弹性运动模型，并从模型的快速计算和自适应步长选取策略2个方面展开论述，提出一种采用2 b深度像素加速的弹性运动估计算法.本文的主要贡献有3个方面：

1) 利用Prewitt梯度算子和梯度模长的均值、标准差提取视频帧的纹理信息，设计了一种将像素从8 b深度向2 b深度进行变换的方法，可避免视频帧在像素深度降采样后出现大面积的光滑区域；

2) 引进基于位操作的矩阵乘法和基于比较操作的偏导运算，提出了一种基于2 b深度像素的弹性运动估计模型，并根据8 b乘法运算的符号表，进一步给出求解该模型的简化高斯-牛顿法，其优点在于用异或操作替代乘法运算，且无需反复计算黑塞矩阵及其逆矩阵，计算复杂度明显降低；

3) 根据运动补偿误差的分布特性，利用1阶线性逼近策略，推导出高斯-牛顿法的自适应步长与弹性运动向量增量、运动补偿误差之间的函数关系，进而得出其近似计算方法，保证了算法具有较稳定的收敛性.

1 相关工作

弹性运动模型采用离散余弦函数、小波函数和样条函数等调和函数来描述物体的非刚性运动，最初主要应用于医学影像配准、物体跟踪等领域.文献[16-17]将弹性模型引进视频编码中，提出了基于弹性模型的运动估计，在相同码率下获得了比块平移运动估计高出0.70 dB的运动补偿峰值信噪比(peak signal-to-noise ratio, PSNR)；文献[18]的结论显示，弹性运动模型可将H.265的输出码率降低3%～12%；文献[19-20,22]则通过优化弹性模型的求解方法取得了更加理想的预测效率，将传统弹性运动估计的平均PSNR又提高了1.42～1.77 dB，比基于块平移模型的全搜索算法高出1.73～2.54 dB.然而，上述文献均采用高斯-牛顿法来迭代地求解弹性运动模型，在每次迭代过程中需计算偏导数、黑塞矩阵、逆矩阵和矩阵乘法，其计算复杂度甚至高于块平移模型的全搜索(full search, FS).尽管经过文献[19-20,22]改进后的弹性运动估计仅需2～3次迭代即可达到块匹配全搜索的补偿质量，可是仍然无法避免黑塞矩阵及其逆矩阵等的反复求解，计算量约为FS的25.62%，高于菱形搜索(diamond search, DS)和测试域搜索(test zone search, TZSearch)等快速块匹配运动估计.

为了增强高阶运动模型求解的实时性，文献[23]提出一种1 b深度像素的高斯-牛顿迭代法，并将其应用到基于6-参数仿射变换的图像配准中.然而，由于1 b匹配误差曲面的梯度较小，该算法至少需迭代50次才能缓慢趋于收敛，计算复杂度并未显著降低.文献[24-25]进一步将文献[23]的思路推广到2 b深度像素，实现了一种基于仿射模型的2 b全局运动估计.可是，为节省逆矩阵的计算量，该方法要求保持迭代步长固定不变，无法实现自适应，且只能朝着单一方向进行迭代.而文献[19-20,22]的研究结论却表明，高斯-牛顿法对初始迭代步长和迭代方向均较为敏感，这就不可避免地导致文献[24-25]在大多数情况下都无法求解出全局最优解.同时，文献[23-25]均利用8 b深度表示的图像计算1阶偏导，再结合经过位截断后的低位深度图像得到匹配误差和最速下降方向.由于低位深像素的梯度往往不同于8 b深度像素，两者混合作用很难保证下降方向的准确性；另一方面，文献[26-27]指出，匹配误差往往产生在较低的位，直接截断低位无法有效保留图像的边缘特征，还将使位于最佳匹配块周围的一定区域内的所有像素被量化成相同值，以致失去对最优向量的判断能力.综合来看，无论是运动估计的精度，抑或收敛速度，文献[23-25]的方法尚不够令人满意，且只能求解仿射模型下的运动向量.因此，研究更加有效的、基于低位深度像素的高斯-牛顿法和弹性运动估计，有助于以弹性模型为代表的高阶运动估计走向实用，对新一代视频编码的发展具有一定意义.从本文作者所掌握的文献来看，目前尚鲜见相关研究.

本文提出的2 b深度像素的弹性运动估计，利用梯度均值和标准差提取图像的边缘和纹理特征，将像素从8 b深度向2 b深度进行转换，并实现了基于位操作的快速高斯-牛顿优化求解.不仅解决了初始迭代步长的自适应选取和迭代方向的多样性，也使得1阶偏导与最速下降方向均在2 b深度像素域进行统一计算，从而保证基于低位深像素的弹性运动估计精度和收敛速度.

2 弹性运动模型及其高斯-牛顿求解方法

为便于下文工作的论述，本节首先介绍弹性运动模型的定义，再给出求解弹性运动向量的高斯-牛顿方法.

2.1 弹性运动模型的基本定义

视频运动估计的目标是在参考帧的某个搜索窗口内，为当前待预测块I(尺寸为B×B像素)搜索到1个运动向量，使得I与其最佳匹配块R之间的误差平方和(sum of squared difference, SSD )最小，即：

(1)

其中，xij和yij分别表示当前待预测块中i行j列像素的x坐标和y坐标，m表示某种运动模型w下的运动向量.对于弹性运动模型，采用弹性基函数φk建立待预测块中每个像素的坐标及其匹配像素的坐标映射，其定义为

(2)

(3)

其中，p表示运动矢量的分量数目，mk表示m的第k个分量，且φk为离散余弦函数：

φk(i,j)=φk+p2(i,j)=

(4)

2.2 弹性运动模型的高斯-牛顿解法

为了获得弹性运动向量m，文献[16-20]均采用了高斯-牛顿法进行求解，主要思想是对匹配误差函数进行线性逼近，再通过反复迭代求出极小值.具体地，假设当前迭代点为m，并令(xij,yij)处的预测误差为eij(m)=R(w(xij,m),w(yij,m))-I(xij,yij)，则eij(m)可用其在m处的1阶泰勒展开式近似表示，即：

(5)

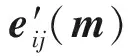
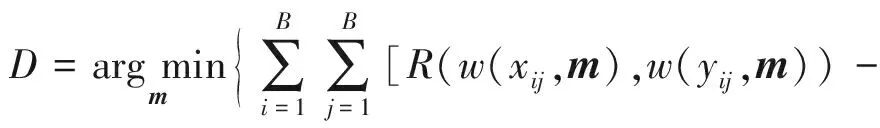
(6)

为取得式(6)的最小值，将其对Δm取导并令导数为0，整理后得到：

(7)

(8)

(9)

显然，H是1个p×p阶的黑塞矩阵，并且根据求导的链式法则和eij(m)、式(2)、式(3)的定义，有：

(10)

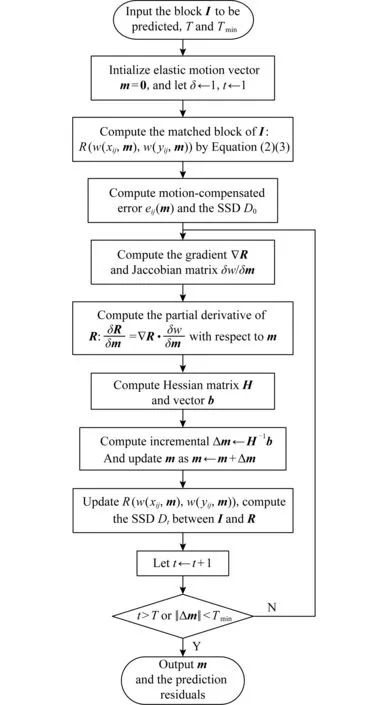
Fig. 1 Flowchart of elastic motion estimation usingthe Gauss-Newton Method图1 基于高斯-牛顿法的弹性运动估计流程图

3 基于Prewitt梯度算子的2 b变换

由2.2节可见，弹性运动模型的高斯-牛顿解法需反复计算偏导数、黑塞矩阵、逆矩阵和矩阵乘法，计算量明显高于块平移模型的全搜索.为此，我们引进基于低位深度像素的策略，将像素从8 b深度降采样为2 b深度，以达到降低计算开销的目的.

3.1 本文的2 b变换算法

将像素从8 b深度转换至2 b深度，势必会丢失视频帧的部分信息，尤其是细腻的纹理细节，产生大面积的平滑区域，这是导致基于低位截断的低位深度像素运动估计出现性能下降的重要原因[26-27].故此，在像素深度变换过程中尽可能保持视频的纹理特征，对于衡量像素深度降采样的有效性、保证运动估计精度具有重要意义.为了达到这一目的，我们首先通过Prewitt算子计算待预测帧的梯度；其次，假定像素梯度的模长服从正态分布，若用均值μC和标准差σC将概率密度划分为4个区间，则知梯度模长位于区间(-∞,μC-0.68σC)，[μC-0.68σC,μC)，[μC,μC+0.68σC)，[μC+0.68σC,+∞)的概率均近似等于0.25，根据这一规律，本文以像素块为单位，将每个像素处的边缘和纹理强度平均分为弱、较弱、较强、强4个等级，从而实现将像素(x,y)的深度从8 b变换为2 b：

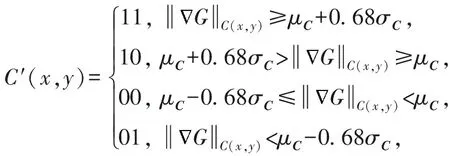
(11)

本文提出的基于梯度均值和标准差的2 b变换过程如图2所示：

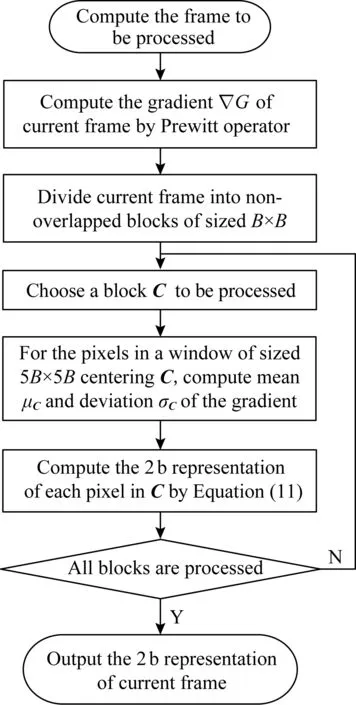
Fig. 2 Flowchart of the proposed 2 b transform图2 本文提出的2 b变换流程图

图3给出了分别采用低位截断方法[28]、基于亮度均值和方差的2 b变换方法[29]，以及本文方法处理Football序列和Foreman序列第2帧的结果.从图3不难发现，基于低位截断的变换方法损失了Football序列包含的复杂背景纹理(图3(b))；虽然基于亮度均值和方差的2 b变换方法[29]在一定程度上避免了位截断方法的不足，可是未充分考虑正态分布的特点，选用亮度均值μ、标准差σ及其线性组合μ-σ和μ+σ作为变换阈值，这将导致约有68%的像素会从8 b深度被降采样为00和01，产生较大面积的平滑区，如Football的运动员身体和Foreman的脸部区域中大量像素被转换为相同值，易使运动估计陷入局部最优，甚至失去对最优向量的判断能力；而本文方法无论在复杂的背景纹理区，还是在平滑的渐变区(如Foreman的脸部)，均能保持适当的图像细节，进而形成能有效区分错误运动向量的特征.

Fig. 3 Comparison among different 2 b transform results图3 不同的2 b变换方法的效果对比

3.2 2 b深度像素的匹配误差曲面的特点

由于位深度变换过程难免丢失少量纹理细节，会出现2种情况：1)当一定区域内的像素均被变换为相同值时，像素值的变化率降低、自相关系数增大.这样，当待预测块在该区域内搜寻最佳匹配块时，匹配误差的变化趋于平缓.我们称这样的区域为“曲面平滑区域”.2)在2个曲面平滑区的交界线两侧，像素值被变换为不同值，像素值的变化率提高，而自相关系数减小.对2 b深度的像素而言，由于匹配误差的值域显著小于8 b深度像素，即使匹配误差增加1，也意味着25%的增幅，这相当于8 b误差增幅的32倍.因此，在交界区域中不同候选向量的运动补偿误差易产生较大变化.2 b匹配误差曲面的这种“区域内平滑、区域间锐化”的分布特点，会使其呈现更加明显的单调性和梯度变化.

图4给出了Stefan序列第2帧内左上角坐标为(144,112)的块和Football序列第2帧内左上角坐标为(176,176)的块，分别进行基于8 b深度像素和基于本文2 b深度像素的整数精度全搜索后得到的匹配误差曲面，搜索窗口为33×33.对比可见：首先，8 b深度像素的匹配误差曲面(图4(a)(c))较之2 b深度像素的匹配误差曲面(图4(b)(d))具有更强的波动性，局部极值点也更多，易导致典型的快速搜索陷入局部最优.其次，在曲面平滑区域，8 b深度像素的匹配误差的变化幅度和频率均大于2 b深度像素的匹配误差；而在极值点的一定邻域以及2个局部极值区域的交界，8 b深度像素匹配误差的变化趋势却较平滑，其数值梯度和衰减速度明显小于2 b深度像素的匹配误差曲面.这不仅印证了上一段的理论分析，也充分说明2 b深度像素的运动估计陷入局部最优的概率更小，且能通过梯度下降策略以更快的速度向全局最优点收敛，尤其是当搜索初始点较为准确、位于全局极值点的单调区间时，从而有利于提高运动补偿精度和运动估计效率.

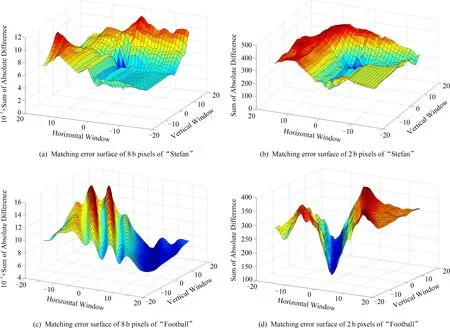
Fig. 4 Comparison between matching error surfaces of 8 b pixel and 2 b pixel under full search图4 8 b全搜索与2 b全搜索的匹配误差曲面比较

4 低位深度的弹性运动模型

传统高斯-牛顿法的每次迭代都需要计算待预测块的偏导数、黑塞矩阵、逆矩阵、矩阵乘法和运动补偿误差等，其计算复杂度达到了max{O(p3),O(p2B2)}.若能降低反复执行上述操作的运算量，则可进一步改善弹性运动估计补偿的效率.同时，经过第3节的处理，视频帧的全部像素已由8 b深度降采样到2 b深度，若继续延用传统高斯-牛顿法中基于8 b整数的偏导、矩阵乘法等运算，则达不到通过精度下采样来提高计算效率的目的.故此，本文对匹配误差eij(m)及其1阶偏导数也进行了位深度变换，利用异或运算取代乘法运算，提出了面向低位深度像素的弹性运动模型，从而加快弹性运动估计的速度.

(12)

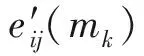
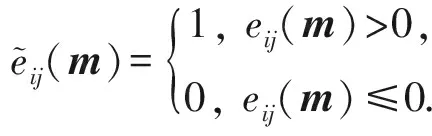
(13)

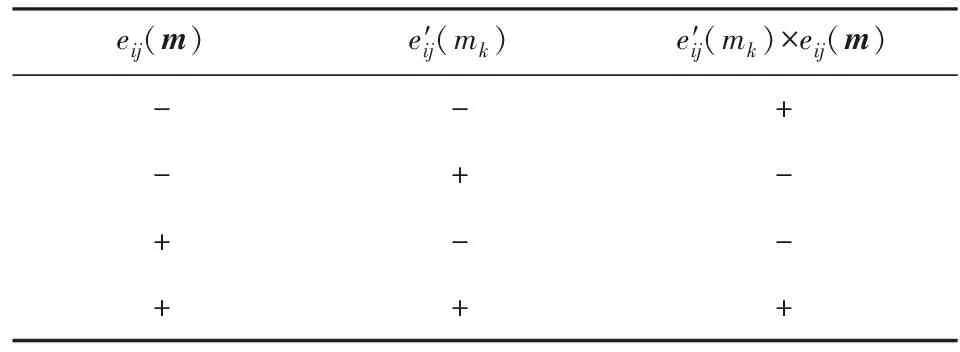
Table 1 Sign of 8 b Multiplication Operation表1 8 b乘法运算的符号表

Table 2 Truth Table of 1 Bit-Wise XOR Operation表2 1 b异或运算的真值表

为了解决这个问题，本文通过将匹配误差进行2次互为相反数的2值化转换，提出了基于2 b深度的弹性运动模型，即：

(14)

(15)

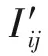
(16)

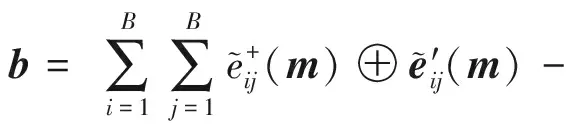
(17)

Table 3 Truth Table of Improved XOR Operation表3 改进的异或运算真值表

5 迭代步长的自适应计算

Δm=-s×sgn(b),

(18)

其中，sgn(·)表示符号函数.但是，这种做法无异于放弃了黑塞矩阵对高斯-牛顿迭代过程的控制.而文献[19-20,22]的研究结论却表明，高斯-牛顿法对初始迭代步长较为敏感，文献[25]的这种固定初始步长的方式显然不利于迭代过程收敛到全局最优解.为了验证这一推论，我们选取Akiyo，Tempete，Football这3个运动特性和纹理复杂度各异的视频序列的前10帧，应用固定步长的2 b深度弹性模型进行了运动估计补偿实验.图5给出了在不同的初始步长s下，3个序列经过15次迭代后所获得的平均运动补偿PSNR曲线.从图5可见，Akiyo序列的运动幅度很小、画面纹理细节简单，随着初始步长的缩小，该序列的运动补偿PSNR明显升高(图5(a))，但是即使初始步长缩小至1×10-6，仍未取得最高的PSNR；Tempete序列的运动幅度中等，可是纹理细节复杂，且包含摄像机的拉摄运动，其运动补偿的平均PSNR在初始步长为4×10-6时取得极值，然后随着初始步长的增大迅速下降(图5(b))；Football序列既包含快速的前景运动和中等复杂度的纹理，又存在物体的局部形变，它在初始步长等于3×10-5时取得了运动补偿PSNR的极值(图5(c))，而此时，Akiyo的平均PSNR已比其最高值下降了4.74 dB.

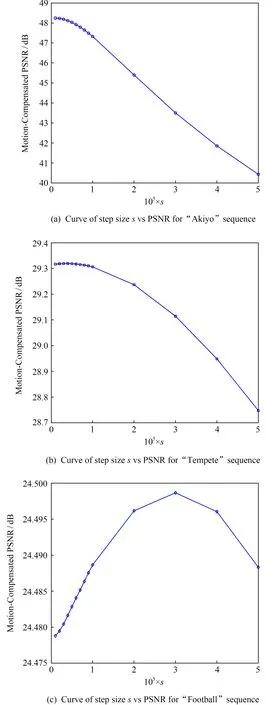
Fig. 5 The motion-compensated PSNR comparison among with different initial step size s图5 不同初始步长s下的运动补偿PSNR对比

对比这3个视频序列的实验结果可知，不同序列的最优初始步长相差几十倍.对于运动幅度较小、画面细节较多的视频，应为其选取一个较小的迭代步长；反之，对于运动速度较快、局部形变较多的视频，为其设定一个较大的迭代步长则更加合适.可见，文献[25]固定初始步长的方式不仅无法保证运动补偿的质量，而且在现实中亦很难做到折中选择.为此，本节采用一种自适应步长s来近似H-1，下面讨论其计算方法.

由式(6)可知，高斯-牛顿法的基本思路是在每次迭代中利用2次函数来逼近匹配误差D(m)，并求解近似函数的极小点作为下一个迭代点，则第k+1次迭代的弹性运动向量mk+1有：

mk+1=mk+H-1b,

(19)

(20)

(21)

(22)

而由微分的1阶近似性质Δf(x)≈f′(x)·Δx，可知：

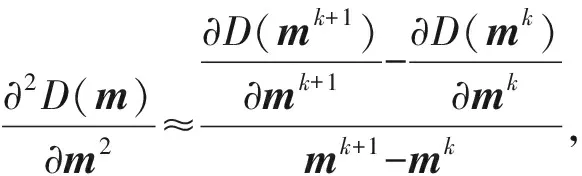
(23)

进一步，将式(20)代入式(23)，得到：

(24)

再由式(22)易知H≈-ΔbΔm，整理后即可得到自适应步长s：

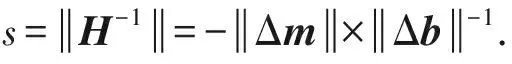
(25)

式(25)表明：自适应步长s与运动向量的变化量Δm成正比，而与匹配误差的变化量及其关于m的导数呈反比.对比图5的实验结果，Akiyo序列的运动幅度很小，其Δm几乎为0，而由于播音员的头部和嘴部存在局部运动，第1次迭代后产生的匹配误差必然大于0，这就使得该序列的最优初始步长趋近于0；尽管Tempete序列存在中等幅度的运动(即Δm>0)，可是复杂纹理细节势必产生较大的匹配误差，故此，由式(25)可推知Tempete序列的最优初始步长也相对较小；考虑到Football序列包含快速运动，其Δm将明显超过Akiyo和Tempete，且纹理细节的复杂度一般，匹配误差变化量在预期上不会显著大于Tempete序列，于是Football序列的最优初始步长较大.综合上述分析，式(25)的结论与图5的实验结果一致.

为了进一步降低式(25)所需要的计算量，本文采用取绝对值运算代替乘法和开平方运算来近似取模长运算：

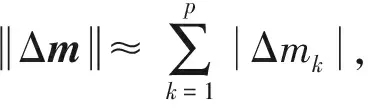
(26)

(27)

其中，Δmk，Δbk分别表示Δm和Δb的第k个分量.同时，本文仅利用式(25)～(27)确定初始迭代步长，而对于后续的迭代，为保证算法具有较稳定的收敛性，本文在步长值满足以下条件时将其减半[25]：b的符号在连续3次迭代中改变3次，即在某个解的局部邻域内发生往返式的迭代.如第4节所述，本文的低位深度的弹性运动模型能朝着2个不同方向进行迭代，若发生折返式迭代，则表明算法很可能处于某个全局局部最优解的单调区间内，且当前步长较大，导致每次迭代均越过该最优解，故应选取更小的步长向这个解进行逼近.

6 2 b深度像素的弹性运动估计步骤

在第5节算法的基础上，本节给出一种基于2 b深度像素的弹性运动估计方法，具体步骤如图6所示，其中，xi，yi表示I中某个像素的横、纵坐标，0≤xi,yi≤B-1；m0表示只包含平移分量的初始运动向量，且m0=(m1,0,…,mp2+1,0,…)；Th表示预设的迭代次数阈值；R′(·)表示参考帧中位于坐标“·”处的2 b深度的像素值；8 b深度像素的菱形搜索和弹性运动估计的搜索窗口尺寸为W×W像素.

Fig. 6 Flowchart of the proposed 2 b elastic motion estimation图6 本文提出的2 b弹性运动估计流程图

7 实验结果与分析

为了验证本文算法的有效性，以通用中间格式(common intermediate format, CIF)、4CIF和高清格式的34个标准视频序列(见表4)的1～90f为例进行实验，并将结果与基于8 b深度像素的菱形运动估计[31](简称8 b-DS)、基于8 b深度像素的块平移全搜索(简称8 b-FS)、基于8 b深度像素的弹性运动估计[16](简称8 b-Elastic)、基于传统2 b深度像素的块平移全搜索算法[29](简称2 b-FS)以及未引进自适应初始步长的本文算法(简称2 b-Elastic-NAStep)进行比较.

实验参数选取为：搜索窗口为33×33像素，宏块尺寸为B=16像素，这与文献[16,29,31]的参数取值相同，也是视频编码器的典型设置.为了在预测精度和收敛速度之间实现折中，令迭代次数阈值Th=5，7.2节还将对此进行深入讨论.同时，为公平起见，将传统8 b-Elastic的迭代次数也设置为5次.运动补偿质量采用PSNR进行评价.

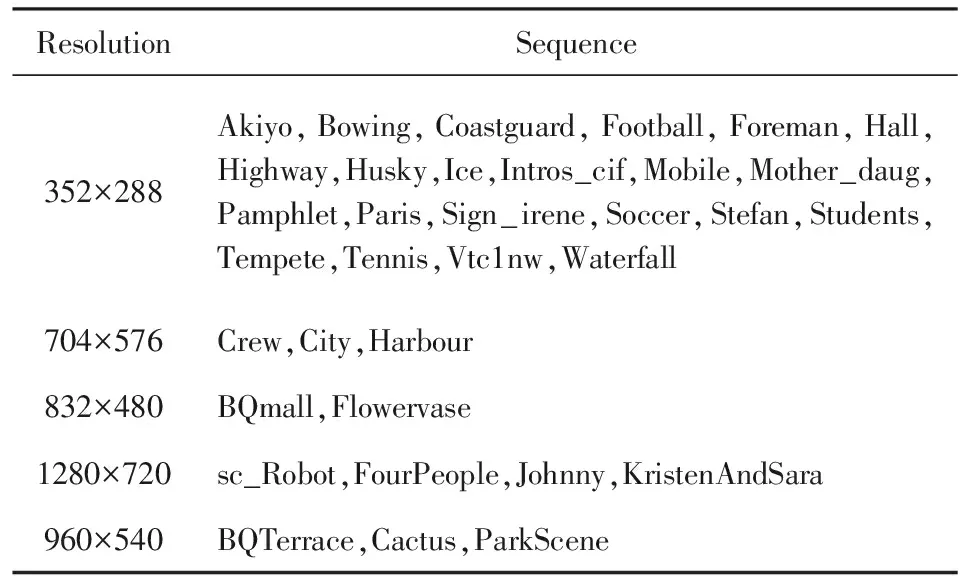
Table 4 Test Video Sequences’ Names and Their Formats表4 测试视频序列名称及其格式

7.1 运动估计补偿质量的比较

表5罗列了各个测试序列的亮度分量采用不同运动估计算法所得到的平均PSNR.从表5可见，相对于传统的2 b深度像素的全搜索算法2 b-FS[29]，未引进自适应初始步长的本文算法2 b-Elastic-NAStep将PSNR平均提高了1.15 dB，表明基于Prewitt算子的2 b变换和2 b深度像素的弹性运动模型能够进行更有效的运动估计补偿.2 b-Elastic-NAStep算法的平均PSNR比传统的8 b深度弹性运动估计8 b-Elastic[16]提高了0.46 dB，其根本原因在于8 b像素的匹配误差曲面富含局部极值点，在缺少初始搜索的情况下易陷入局部最优，并且8 b匹配误差曲面的下降梯度为高斯-牛顿法提供的迭代驱动力不足，收敛速度较慢；而2 b-Elastic-NAStep算法则利用8 b-DS计算弹性运动向量的水平和竖直分量，将起始搜索点置入全局最优点的单调区间，再沿着梯度下降方向进行迭代，这表明起始搜索点对于提高弹性运动估计的精度有重要作用，该结论与文献[19-20,22]的研究结果一致.同时，2 b-Elastic-NAStep算法的平均PSNR较之8 b深度像素的菱形运动估计8 b-DS高出0.90 dB，并且比8 b深度像素的块平移全搜索8 b-FS提高0.23 dB，说明本文提出的低位深度弹性运动模型在初始搜索的基础上取得了进一步的性能增益.在引进了自适应初始步长之后，本文算法的运动补偿PSNR比2 b-Elastic-NAStep又提高了0.92 dB，这表明通过自适应步长实现黑塞矩阵对迭代过程的控制，有助于弹性运动估计收敛到全局最优解，进而表现出与8 b深度像素的阻尼高斯-牛顿法相近的准确程度.

图7给出了Akiyo，Husky，City，Flowervase序列的PSNR逐帧比较情况.其中，Akiyo序列仅含有局部慢速运动，且细节简单；Husky序列则与之相反，前景具有较大幅度的平移运动且纹理复杂性高；City序列含有摄像机的中速摇摄运动和丰富的细节信息；而Flowervase序列则包含摄像机的慢速拉摄运动和中等复杂性的纹理.如图7所示，尽管4个序列的运动类型、速度和纹理复杂度各有不同，本文算法的运动补偿质量均较为稳定，在绝大部分情况下都取得了最高的PSNR，而其他算法的运动估计精度却会随着视频特点的不同出现一定波动.

Table 5 Motion-Compensated PSNR Comparison表5 运动补偿的PSNR 比较

Fig. 7 PSNR comparison among different algorithms on the first 90 frames of Akiyo, Husky, City, and Flowervase图7 Akiyo,Husky,City，Flowervase的前90帧采用不同运动估计算法所得到的PSNR比较

需要指出，作为逆黑塞矩阵的1阶近似，本文的自适应步长对于前景运动慢、纹理细节简单或者含有慢速摇摄、拉摄运动的视频(如Akiyo,Johnny,Flowervase)尤为有效，而对于含有快速运动和复杂纹理的视频(如Husky和City)，其性能增益则不够明显.究其原因在于，后者的匹配误差曲面非常复杂，导致每次迭代的最优步长之间存在较大差异，尤其当迭代过程从搜索起始点所在的单调区间进入其他单调区间时，初始步长的普适性难免会受到影响.这也是除了像素深度降采样这个原因以外，本文算法在Mobile，Waterfall，Harbour等序列上的运动补偿PSNR低于传统8 b-Elastic运动估计的根本缘故.当然，作为一种基于低位深度像素的快速运动估计算法，本文工作的基本目的是在计算量和运动估计精度之间尽量实现折中，而不是通过精确估计阻尼步长来取得最理想的补偿质量.从这个意义上讲，本文提出的低位深度的弹性模型及其初始步长的自适应计算能够满足较低计算负载下的弹性运动估计需要.

7.2 收敛速度与迭代次数的讨论

收敛速度是衡量弹性运动估计效率的指标之一.图8所示为Akiyo，Husky，City序列第2帧采用本文算法的前15次迭代结果.从图8中能够发现，对于运动幅度小、细节简单的Akiyo序列，本文算法在第1次迭代后就趋于收敛；对于运动幅度较大、纹理复杂的Husky序列，运动补偿的PSNR随着迭代次数的增加而不断升高，但是经过5次迭代就已达到最高PSNR值的99.97%；而对于含有摇摄运动且纹理丰富的City序列，本文算法在第8次迭代时取得了最高的运动补偿质量，之后出现PSNR的下降，不过在第5次迭代后已达到PSNR峰值的99.99%；由于Flowervase序列的情况与City类似，这里不再赘述.图8结果表明，一方面，本文算法在视频具有不同运动模式和空间分布特点的情况下，均能取得较快的收敛速度.另一方面，视频的运动幅度和模式，以及空间纹理复杂性对本文算法的收敛速度存在一定影响：当匹配误差曲面在全局局部最优解附近呈现单峰分布时(如Akiyo)，本文算法将快速收敛，这与3.2节所讨论的2 b匹配误差曲面具有“区域内平滑、区域间锐化”的分布特点一致，下降梯度能提供足够的迭代驱动力；反之，当迭代过程需越过不同的单峰区间时，可能引起运动补偿质量的波动甚至小幅下降.这种情况与7.1节末尾的讨论一致，源于本文为了节省计算量，仅求解1次自适应步长并且未对相邻2次迭代的均方误差进行比较(若设1个视频帧包含N个像素，则计算均方误差的时间复杂度为O(Th×N)).

Fig. 8 Result of the second frame of Akiyo, Husky, and City during the first 15 iterations图8 Akiyo,Husky,City的第2帧的前15次迭代结果

7.3 计算复杂度分析

设宏块尺寸为B×B像素，搜索窗口为W×W像素，则不同运动估计算法处理1个宏块的计算量为：

1) 8 b-FS和2 b-FS的时间复杂度均为O(B2W2).另外，2 b-FS在像素深度变换阶段还需O(B2)的复杂度.

2) 由文献[31-32]可知，8 b-DS的计算复杂度约为8 b-FS的7%，即O(0.07B2W2).

3) 用高斯-牛顿法求解8 b深度弹性运动模型的每次迭代需计算偏导数、黑塞矩阵、逆矩阵、矩阵乘法、双线性插值和当前的运动补偿误差，其渐近时间复杂度分别为O(pB2)，O(p2B2)，O(p3)，O(pB2)，O(B2)，O(B2).

4) 由于省去了黑塞矩阵及其逆矩阵的计算，本文算法的每次迭代过程只需求解偏导数、向量乘法、双线性插值和运动补偿误差，其渐近时间复杂度分别为O(pB2)，O(pB2)，O(B2)，O(B2)，基于菱形搜索的初始点预测还需约为O(0.07B2W2)的计算复杂度.

当搜索窗口W=33、块尺寸B=16、迭代次数阈值Th=5时，本文算法的时间复杂度约为8 b-FS算法和2 b-FS算法的15.26%、8 b-Elastic算法的39.58%，但是高于8 b-DS.若进一步将迭代次数Th减少到2～3次，本文算法则可在8 b-FS算法的10.31%～11.60%的时间复杂度内，获得与之相当的运动估计精度.

具体地，表6给出了各种算法求解1个块的运动向量所需的平均操作次数，其中运动估计阶段的“Addition”操作包括8 b定点加法和浮点加法.从表6可见，本文方法的操作次数显著少于8 b-FS，2 b-FS和8 b-Elastic.尽管8 b加法、2 b加法、乘法、取绝对值、比较、位运算等各类操作所需的CPU周期数和计算代价存在明显差异，可是这些指标依赖于具体的硬件设计和指令集，已超出本文的讨论范围，所以在此不予进一步的定量比较，详细了解可参见文献[28].不过，考虑到本文算法采用位操作和比较操作来求解偏导数、向量乘法和运动补偿误差，其计算开销将低于8 b像素的加法和乘法，且有利于实现多个像素的并行计算，其实际开销比渐近时间复杂度更低.

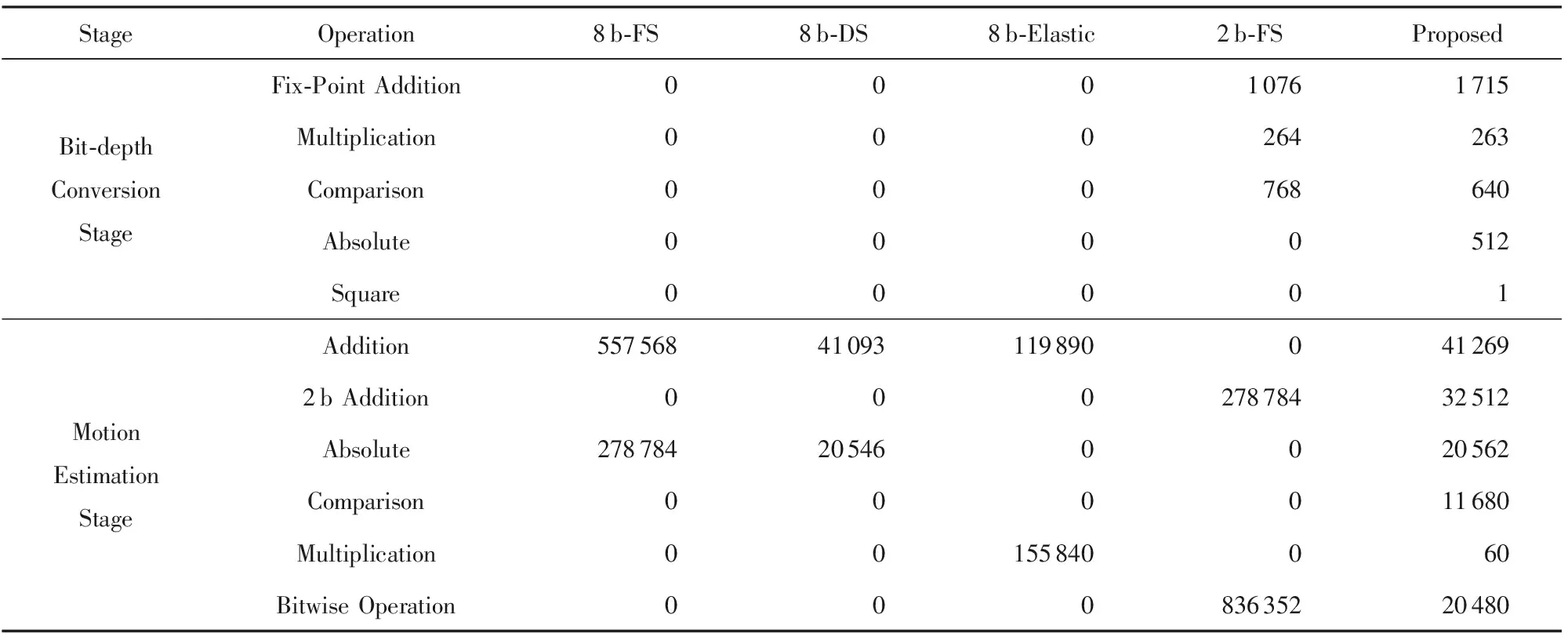
Table 6 Average Operation Number Comparison Among Various Motion Estimation Algorithms on Each Block表6 不同运动估计算法对每个块的平均操作次数比较

8 结 论

为进一步改善弹性运动估计的实时性，本文引进了基于Prewitt梯度算子和正态分布的像素深度变换，以及基于位操作和比较操作的矩阵乘法和偏导运算，推导出高斯-牛顿法的自适应初始步长的1阶逼近方法，从而提出了一种基于2 b深度像素的弹性运动估计.其优点在于尽可能地简化求解弹性运动模型的高斯-牛顿法，用异或运算替代乘法运算，且无需反复计算黑塞矩阵及其逆矩阵.实验结果表明，该算法的运动补偿质量和计算效率优于8 b深度像素的块平移全搜索算法、菱形搜索算法、传统弹性搜索算法，以及传统2 b深度像素的块平移全搜索算法.

另外，本文算法仍存在若干问题可臻完善，如快速预测起始搜索点、根据匹配误差曲面的曲率变化来自适应地更新初始步长，以及设计能够高效执行本文算法的硬件电路等，我们将在今后的工作中进一步深入研究这些问题的解决思路.