“探索直线平行的条件”教学设计与评析

谭军振

一、教学目标

1.对同位角进行正确识别;2.掌握直线平行的原理：两条直线被第三条直线所截，同位角相等，则两条直线平行;3.探索直线平衡过程，并建立空间观念，具有一定的表达能力。

二、教学重、难点

重点内容：1.对同位角进行识别;2.将同位角应用于两条直线平行判断中。

难点：直线平行的探索，空间观念及表达能力的培养。

三、教学过程

（一）情境引入

活动一：利用三角尺和直尺画平行线。

学生活动：1.回忆旧知。2.学生上台演示画图;设计思路：以“三角尺和直尺画平行线”为问题情境，探索直线平行的条件：同位角相等，两直线平行。先复习平行线的画法，然后进一步探究直线a，b平行的原因。引导学生观察画出的图形，分析用三角尺和直尺画平行线的过程，得出结论：由于直尺不动，三角尺在平移过程中，其对应角的大小不变（∠1=∠2），因此画平行线实际上就是画相等的角。

（二）新课导入

想一想：通过观察、比较，认识“同位角”，归纳直线平行的条件。

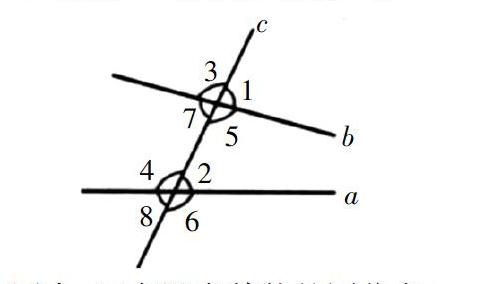
同位角：如下图，在两条直线被第三条直线所截而成的8个角中，像∠1与∠2这样的一对角称为同位角。

议一议：在上图中，还有没有其他的同位角？

观察：∠1，∠2分别在直线a，b的上方，并且都在直线c的同旁。并归纳出同位角特点（两同）：（1）在第三条直线的同旁;（2）在被截两直线的同一方向。设计意图：引导学生归纳，判别同位角时，要注意位置上的两个“同”字，在第三条直线的同旁，被截两直线的同一方向。

活动二：借助问题情境展开教学，三根木条分别用a、b、c表示，a和b交c形成∠1和∠2，转动木条a。设置问题：（1）木条a转动过程中，a和b的位置关系发生怎样的变化？木条a和b与c相交的角度发生怎样的变化？（2）对∠1大小进行改变，当∠1和∠2满足什么关系时，a和b平行？

学生活动：观察、思考，并归纳、小结得出“同位角相等，两直线平行”，并在图形变式中，体会“同位角不相等，两直线不平行”。

设计意图：设置“转动木条”的活动，目的是使学生在操作活动中直观地认识直线平行的条件。结合教学实践来看，两条直线被第三条直线所截，同位角相等，则两条直线平行。即：同位角相等，两直线平行，用符号表示为：∠1=∠2→a∥b.

通过归纳：a和b相交于c，∠1和∠2是同位角，所以得出结论：同位角相等，两条直线平行。本次设计意图如下：让学生对同位角的特征进行了解，理解同位角相等，两条直线平行这一数学原理。通过课堂活动，带领学生进行实践探究。通过动手操作和观察，使学生理解“同位角相等，两条直线平行”这一数学原理。

（三）典型例题：

例1：如图所示，当∠1=∠C，∠2=∠C的时候，请找出图内存在相互平行的直线，并说明为什么？

学生结合问题开展探究活动，并对观点进行表达。

参考答案：∠1和∠C为直线AB、CD被AC所截形成的同位角，并且存在着∠1=∠C的关系，根据定理可知，AB∥CD。又因为∠2=∠C，并且∠2和∠C是直线AC、BD被CD截取形成的同位角，所以AC∥BD。

设计意图：师生互动，锻炼学生的口头表达能力，培养学生勇于发表自己看法的能力，会进行简单的说理。

（四）思维拓展：运用本节课所学数学知识解决生活中的实际问题

（1）木工师傅用角尺在工件上画出工件边缘的两条垂线（如图），这两条垂线平行吗？为什么？（2）由（1）你能得到什么结论？

学生活动：积极思考解决办法——运用本节课所学数学知識解决问题，关键是看同位角是否相等。

设计意图：问题深入，既检测了学生对本节课知识的掌握程度，考查了学生解决问题的综合能力，又让学生在实践中体验“学以致用”的道理。第（1）小题复习巩固学生所学基础知识及基本方法，并进一步提高学生“执果索因”的能力;第（2）小题重在培养学生简单推理的能力。

四、教学设计说明

1.教材分析：直线平行是苏教版七年级数学下册第七章的重点内容，也是本册书的重点内容。平行线在现实生活中比较常见，其对两条直线的位置关系问题进行研究。因此，在开展这一节课教学的时候，直观认识是本节课的教学基础。在教学中，要将学生的观察和推理进行结合，将平行结论应用于实际问题解决当中，增强学生的实践探究能力。

2.学情分析：学生对平行线的知识已经有了一定的了解和认知，能够对两条直线是否平行进行判断，但对理论知识的掌握有所欠缺。针对这一情况，本节课教学的重点在于培养学生推理能力，使学生通过动手操作，对问题进行深入分析，把握平行的基本原理，并能够进行语言表达。

3.设计思想：课堂教学设计突出教师为主导、学生为主体的原则，将直线平行知识进行有效传授，突出学生思维能力的培养。在具体研究中，对学生分类、探究、合作、归纳的能力进行培养，使学生在操作中对平行知识进行理解和认知，以提升学生自主学习能力。

五、课堂小结

本节课围绕直线平行的条件展开了研究和分析，得出结论：同位角相等，两条直线平行。结合本节课及以前所学知识，判断直线平行的方法总计有三种：（1）定义判别;（2）如果两直线都平行于第三条直线，则两直线平行;（3）同位角相等，两直线平行。