具Intraguild捕食的非自治三种群Lotka-Volterra模型的正周期解
2019-11-14陈柳娟
陈柳娟
(福建教育学院,福建 福州 350025)
文[1]研究了一类关于资源竞争的Intraguild捕食的非自治三种群Lotka-Volterra模型(1.1)的持久生存,文章进一步研究模型(1.1)的正周期解。
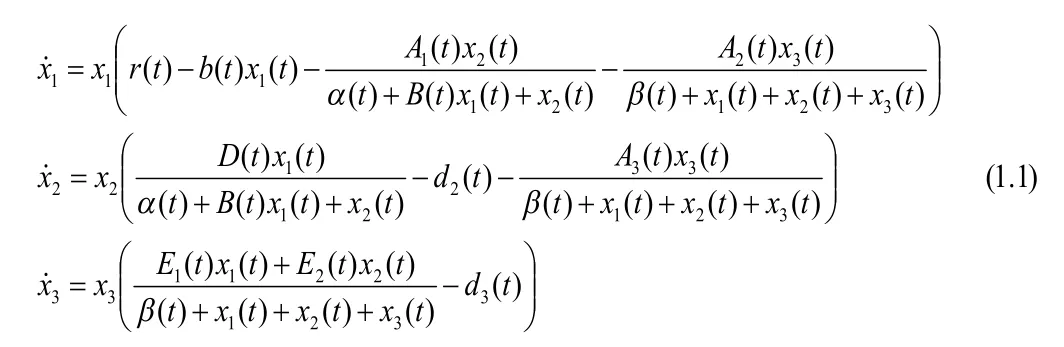
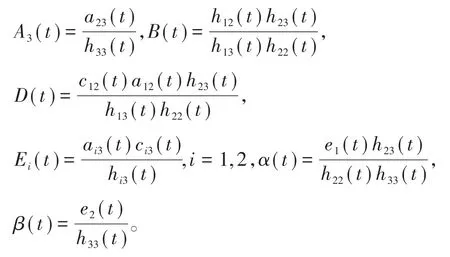
1.引理
设X,Z是赋范向量空间,L:DomL⊂X→Z是一个线性映射,N:X→Z是一个连续映射。如果dimKerL=codim ImL<+∞且ImL是Z中的闭子集,则称映射L是指标为零Fredholm映射。如果L是指标为零的Fredholm映射且存在连续投影P:X→X和Q:Z→Z使得ImP=KerL,ImL=KerQ=Im(I-Q),则L|DomL∩KerP:(I-P)X→ImL可逆,记其逆映射为KP。设Ω为X中的有界开集,若有界且是紧的,则称映射N在上是L-紧的。由于ImQ与KerL同构,因而存在同构映射J:ImQ→KerL。
引理1[2](重合度延拓定理)令L是指标为零的Fredholm映射且N在上是L-紧的。假设
为了方便,记 ,这里g是ω-周期连续函数。
2.主要结果
本节证明模型(1.1)正周期解的存在性,其中所有的参数关于时间t都是连续且是ω-周期的。
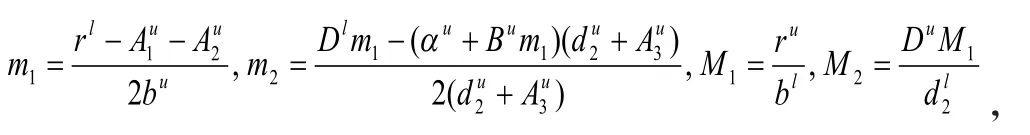
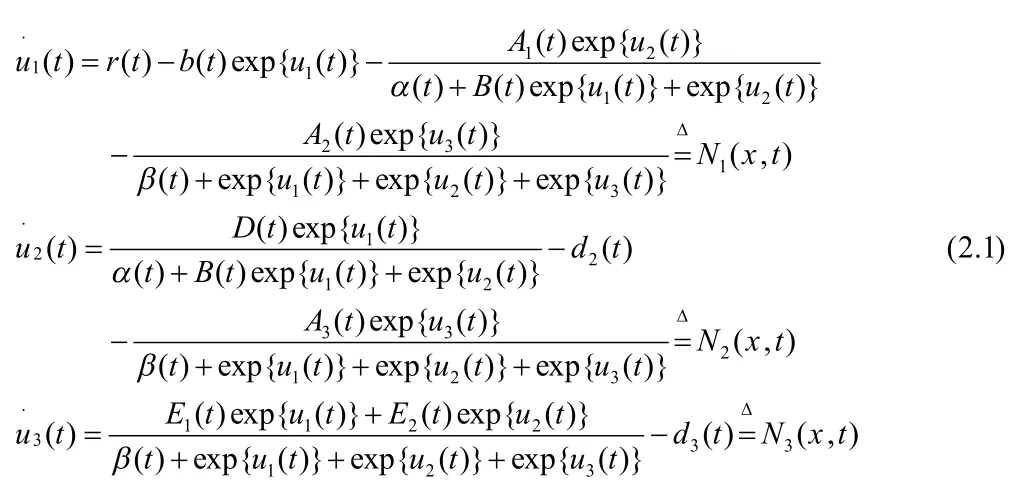
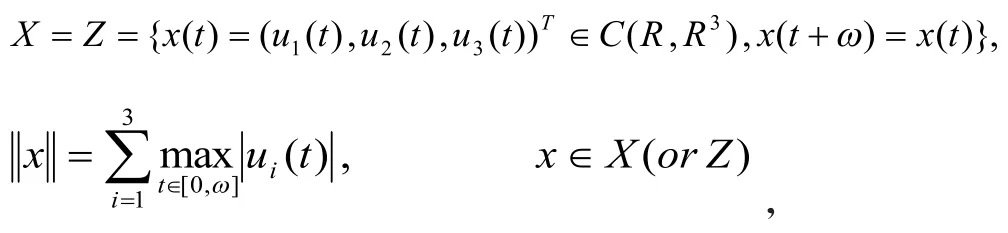

则
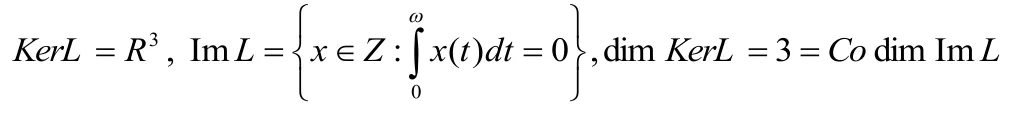
且ImL是Z中的闭集,因而L是指标为零的Fredholm映射。此外,P,Q是连续投影使得ImP=KerL,KerQ=ImL=Im(I-Q),所以L的逆映射KP:ImL→DomL∩KerP存在且
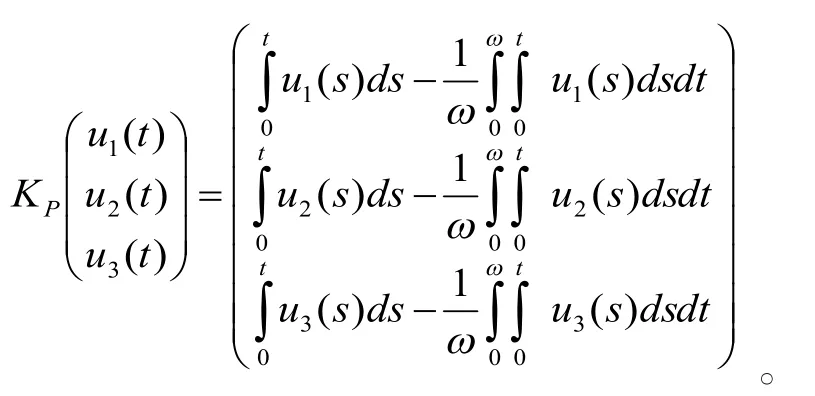
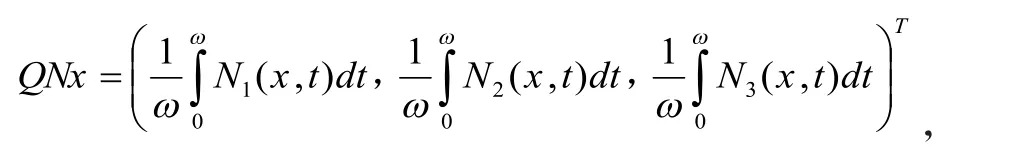
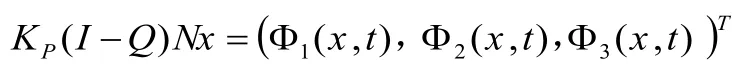
显然,QN和KP(I-Q)N连续且对任一有界开集,有界。由Arzela-Ascoli定理易知是紧的。从而,对任一有界开集,L在上是L-紧的。相应的算子方程,有
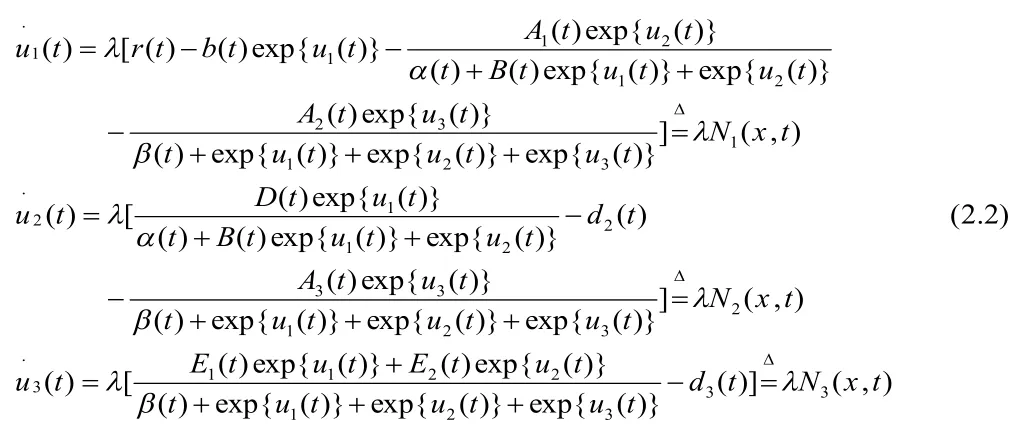

从而有
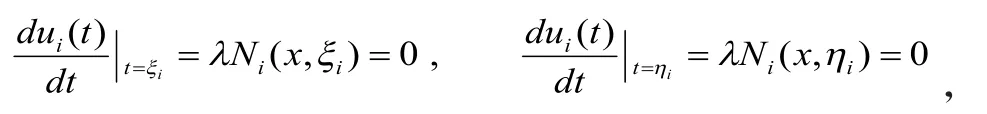
即
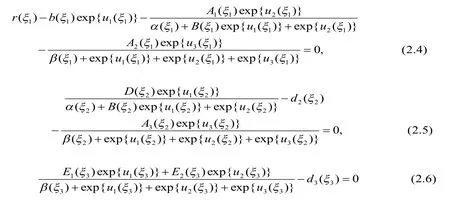
和
由(2.4)和(2.7)可得

由(H2)易知
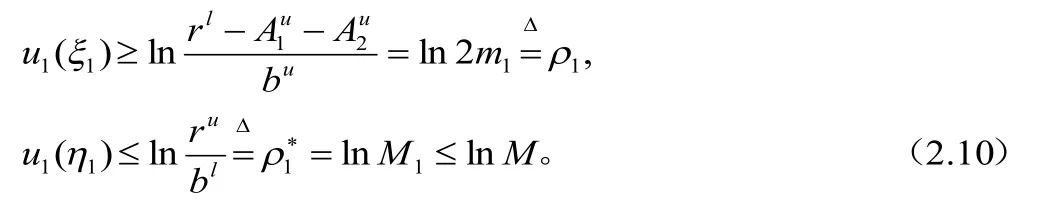
由(2.5)、(2.8)和 (2.10)可得

由(H3)易知
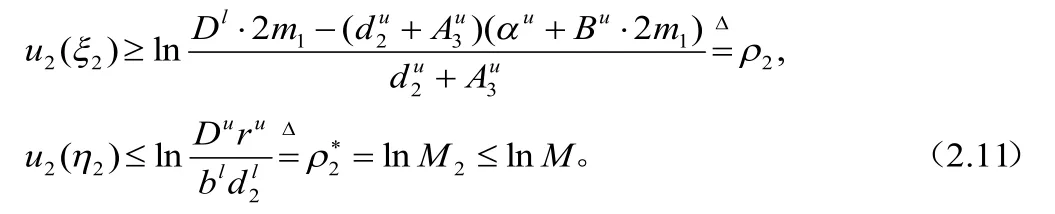
类似地,由(2.6)、(2.9)、(2.10)和 (2.11)可得
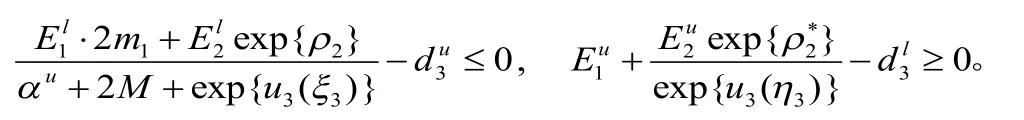
若(H4)成立,显然有,从而,由(H1)和(H4)可得

再由(2.10)、(2.11)和(2.12)可得
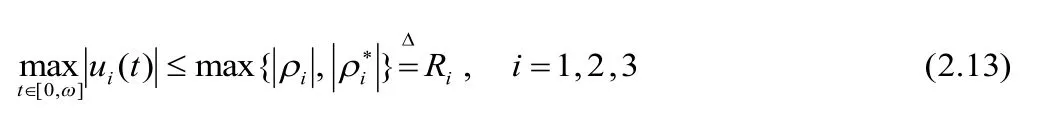
显然,Ri(i=1,2,3)与λ无关。考虑下列的代数方程:

这里μ∈(0,1)是一个参数,(μ1,μ2,μ3)∈R3。如前面类似的讨论可得当μ∈(0,1)时,系统(2.14)的任意一个解满足。
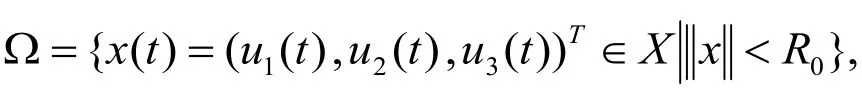
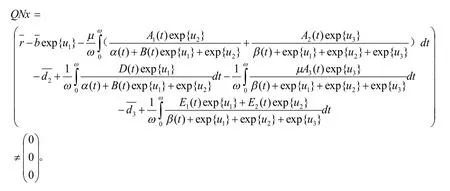
另一方面,考虑同伦
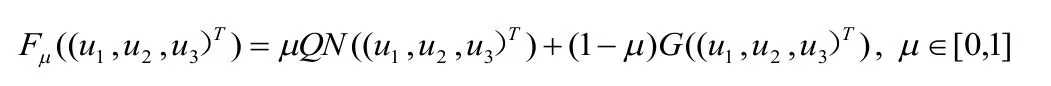
这里

