出租车司机的理性行为决策

赵蕾 西北政法大学

我国的绝大多数机场都是采用出发通道与到达通道相分离的布局，因此，送机的出租车司机在将乘客送达之后便会面临两个选择：直接返回市区或前往到达区载客后再返回市区。若直接返回，司机要付出空载成本，并且可能损失潜在的收益；而载客后返回，则需要付出相应的时间成本。

针对该问题，文中对影响司机做出决策的各种因素进行分析，并在此基础上建立一个能够使司机在不同条件做出决策的数学模型，并通过此模型来实现司机的理性决策的目标。

在众多的决策方法中，层次分析法是将半定性、半定量问题转化为定量问题的有效途径，它将各种因素层次化，并逐渐比较多种相关联的因素，为分析和预测事物发展提供可比较的定量依据。在生活中，影响司机做出决策的因素包括确定信息和经验信息两大类。其中，不同时间段到达的航班数量是司机能够确定的主观因素，通过对一天中的时间段，蓄车池中车辆数目进行划分，建立司机的决策表格，利用层次分析法来计算出通过一致性检验后的权重矩阵，从而建立司机在一天中的决策模型。

通过数据搜集发现一天中0:00～9：00机场的飞机航班数量较少，在30架以下；9:00～17:00和20:00～24:00这两个时间段的航班数量较多，都处于30～53架之间；而17:00～20:00是航班数量最多的时刻，数量达到53架以上。此数据是对2019年7月1日广州白云机场的航班数据统计得知。下面将通过模型的建立来求得该表中Ai的具体数值，以此作为司机进行决策的依据。

首先，我们需要建立司机决策的层次结构模型。出租车司机作为一名理性经济人，其决策目标就是最大限度地实现收益最大化，处于模型中的最高层。为了目标，其在进行决策时就会有两种备选方案-留在蓄车池中等候或者返回市区重新载客，因此这两种方案是该模型的最低层。在司机进行决策时会受到各种因素的影响，我从中选取了四个因素作为影响司机做出决策的关键条件，如图1所示，是我建立的出租车司机决策的层次结构模型。

图1 出租车司机决策的层次结构模型

其次，需要构造判断矩阵。在确定各层次各因素之间的权重时采用一致矩阵法，即：

（1）不把所有因素放在一起比较，而是两两相互比较。

（2）采用相对尺度，以尽可能减少性质不同的诸因素相互比较的困难，以提高准确度。

接着，需要对层次单排序及其一致性进行检验。层次单排序是给出准则层因素对目标层而言相对的重要性(权重)，及其一致性检验，在成对比较过程中允许不一致情况的出现，但需要对不一致的允许范围进行确定。

最后，则是对层次总排序及其一致性进行检验。层次总排序是给出方案层的方案关于准则层的各因素而言相对的重要性，及其一致性检验。

基于以上原理我们对假设条件下的一天中，基于不同的时间段和蓄车池车辆数，对司机的行为决策进行AHP分析，步骤如下：

a.计算归一化权重系数

根据计算公式

计算初始权重系数wi'。

再根据公式

最终计算得到归一化权重系数wi。

b.对权重系数是否符合逻辑进行检验

在确定权系数过程中，依靠主观判断给出的判断矩阵，还需要通过一致性检验，以便尽可能消除人的主观判断所导致的不一致性结果的产生。一致性检验通常采取一致性指标CI 检验该项目的相对优先顺序有无逻辑混乱，一般认为，当CI ＜0.01时，可能逻辑混乱，此时计算所得的各项权重可以接受。

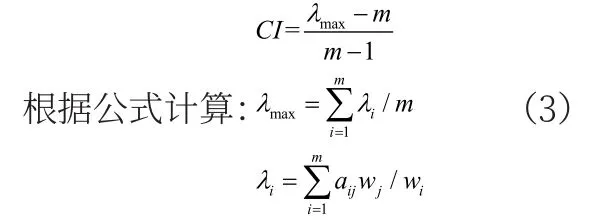
其中式中m为接受检验层次的子目标数，λmax为最大特征根，λi为该层子目标成对比较判断优选矩阵的特征根。

为了进一步度量不同阶段矩阵是否具有满意的一致性，我们仍需要引入判断矩阵的平均随机一致性指标RI。不过，对于1-2阶判断矩阵，RI 只是形式上的，因为1-2阶判断矩阵具有完全一致性。当阶数大于2时，判断矩阵一致性指标CI 与同阶平均随机一致性指标RI之比称为随机一致性比率，记为CR，其中

当CR ＜0.1时，即可以认为判断矩阵具有满意的一致性，否则就需要调整判断矩阵，并使之具有满意的一致性。

基于以上原理，我们计算出不同时间段的12个总排序一致性比率，如表1所示。

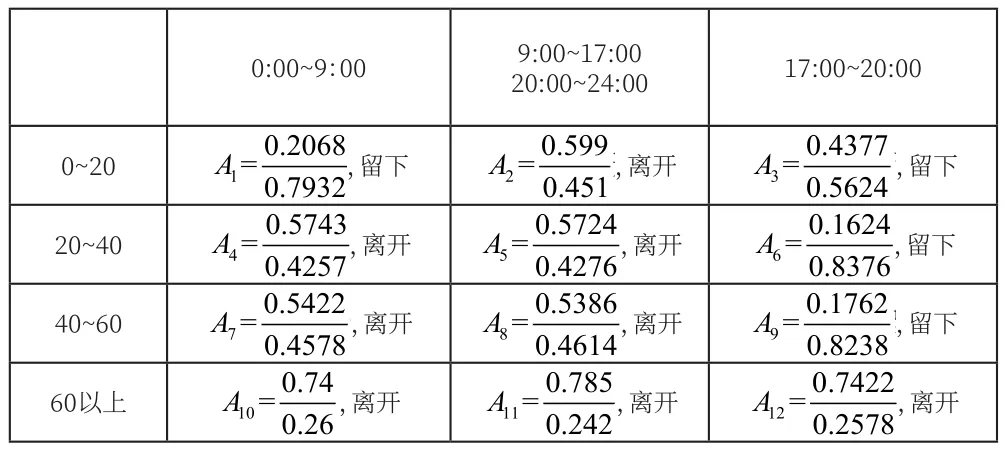
表1 假设条件下的一天中不同情况下司机的决策表格

从此表中可以看出，当天气为阴雨天且处于旅游旺季时，0:00～9：00是航班数最少的时间段，此时司机更多的会选择离开机场返回市区，但如果蓄车池中车辆较少，司机可能就会选择留在机场等待乘客；17:00～20:00是一天中飞机场航班数最多旅客的时间段，此时司机更倾向于留在蓄车池等待乘客，但当蓄车池的车辆较多时，司机则可能会离开机场前往市区。该表中的计算结果基本与我们日常生活中遇到类似情况时司机所做的决策基本相符，因此用该模型来进行不同条件下司机决策的预测是具有一定效果的。但是文中决策表格的列举是有一定的假设前提的，在不同的天气、季节、时间段的因素干扰下，决策表格也会有相应的变动。