一类四阶非线性系统的全局渐近稳定性

原新生

(安阳师范学院 数学与统计学院，河南 安阳 455000)

1 研究背景

S．Kasprzyk[1]在1972年曾致力于下列三个三阶非线性系统

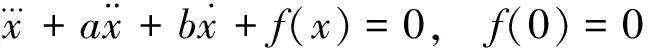
(1.1)

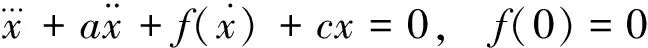
(1.2)

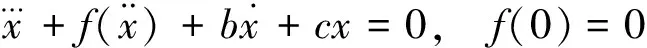
(1.3)

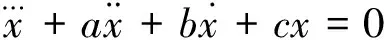
(1.4)

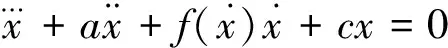
(1.5)

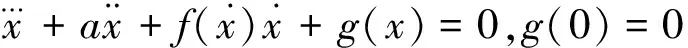
(1.6)

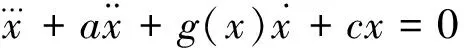
(1.7)

(1.8)

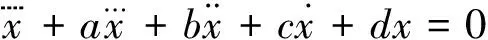
Wall的能量度量算法可归纳为下面六步[9-13]：

第一步，将所描述的系统写成一阶联立的微分方程组

(1.9)

其中x=(x1,x2,…,xn)

第二步，将微分方程组(1.9)写成如下形式

(1.10)

第三步，将微分方程组(1.10)写成

Fj(x)dxi=Fi(x)dxj,j>i

(1.11)

第四步，用适当的代换和加法，将微分方程组(1.11)化为

ω1(x)dx1+ω2(x)dx2+…+ωn(x)dxn=0

(1.12)

第五步，求出V(x1,x2,…,xn),

(1.13)

第六步，求出V(x1,x2,…,xn)的全导数，

(1.14)

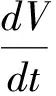
2 主要结果

考虑四阶非线性系统

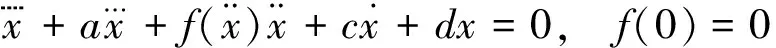
(2.1)

将其化为等价系统

(2.2)

两两分别相除得

(2.3)

即

由(2.4)×2(adf(z)-cd)+(2.5)×2a2d+(2.6)×2ad+(2.7)×2(a2c-ad)+(2.8)×2ac+(2.9)×2c得

(2ad2x+2acdy+2cdz)dx+(2adf(z)y-2cdy+2adu+2acdx+2ac2y+2acf(z)z)dy+(2a2dy+2a2cz-2adz+2cdx+2c2y+2cf(z)z+2acu)dz+(2ady+2acz+2cu)du=0

(2.10)

所以

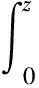
(2.11)

=-2(acf(z)-c2-a2d)z2+adf′(z)uy2

(2.12)

于是，我们得到下述定理：

定理[8]，如果

(1)a>0,c>0,d>0;

(2)acf(z)-c2-a2d≥δ>0;

(3)f′(z)u<0(u≠0)

则系统(2.2)的零解是全局渐近稳定的。