基于数据挖掘的数据聚类分析研究

李 雪

(安徽工贸职业技术学院，安徽 淮南 232001)

数据挖掘的过程就是在大型的数据库中挖掘有用的数据，到目前为止，研究人员已经发现了几种基于被处理数据对象类型的聚类算法，并通过聚类分析来确定聚类分析的目的和实际应用。由于数据对象在计算的过程中具有重叠性，所以不能对聚类算法进行分类，易产生更多类型特征的算法。聚类分析是一种传统的分析方法，它根据具体的需求和规则对事物进行聚类，属于一种具有二元属性的硬聚类。然而，在实际的问题中，属性的划分并不完全严格。Zadeh提出的模糊集理论为这种软分类提供了解决方案。

1 聚类分析的步骤与算法

1.1 聚类的一般步骤

在实际的算法中，聚类分析可以分为三个部分，每个部分规定了具体的任务，这样能够保证整个聚类分析的过程更加清晰。

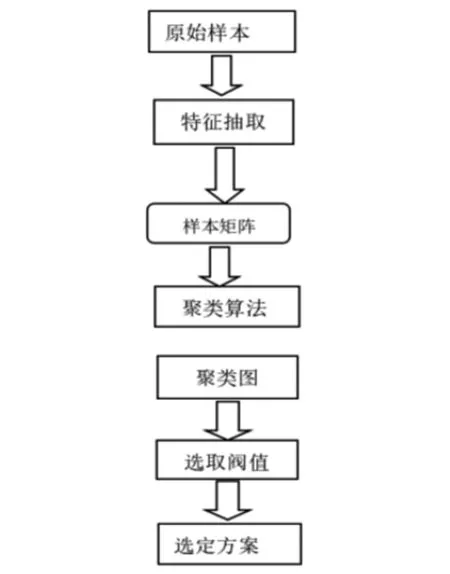
图1 聚类分析步骤

第一步，根据特征进行选择。在初期输入的是原始样本，有相关的算法和人为来决定使用那些具有特征结构的数据，通过输出样本来分析结构和性质。一般数据输出结果是一个矩阵，矩阵中的一行为一个样本，每一列为一个指标，并且指标属于变量，指标特征的选取会直接影响到计算结果。

第二步是执行聚类算法，获得聚类图谱。输入矩阵样本，样本仅仅是矩阵空间中的一个数据点，通过聚类算法来获取样本点与空间之间的簇成性质。

1.2 聚类的数据类型

数据挖掘的一个重要步骤则是数据准备，包括对已选定数据的规范与处理，这是数据挖掘工作的基本前提，也是聚类算法计算的必要条件。对数据对象进行聚类分析，需要计算出每一个对象之间聚类，针对不同的数据类型，有不同的异度计算方法。聚类算法中比较常用的有两种数据结构，数据矩阵和相异度矩阵。

1.数据矩阵。矩阵中的每一个数据代表一个数据结构，矩阵是由n个数据组成的，以人为例，人是由n多个属性组成：年龄、性别、身高、体重等等。而数据矩阵采用的关系类别也是对应关系，如图2所示。

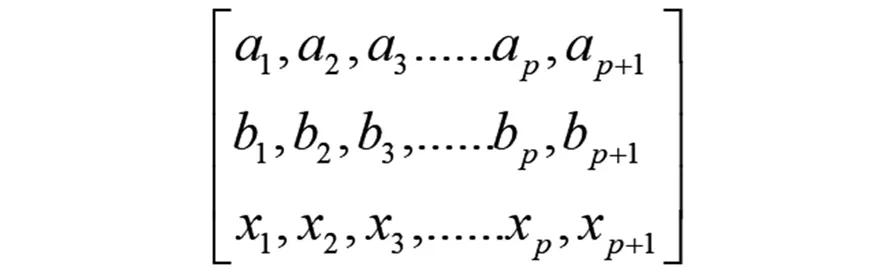
图2 矩形数据

2.相异度矩阵。相异度矩阵是一个对象一个结构，在矩阵中有n个对象两两之间所形成的差异，一般采用n*n的矩阵关系来表示。

其中f(p,q)代表着对象p和对象q之间的差异，通常f(p,q)代表着一个非负数，当p,q无限接近的时候，数据接近于0，数值越大，代表p,q两个数据不接近，如图3所示。

图3 相异度矩阵

一般来讲，数据矩阵通常又被称为双模式矩阵，相异度矩阵被称为单模式矩阵。前者与后者的实体不同，但是后者与列表示的则是统一实体。许多聚类算法是基于相异度矩阵计算出来的，然后再利用聚类算法进行处理。

1.3 最近邻优先聚类算法分析

1.NNAF算法。NNAF算法是短距离聚类算法，其基本思想是把两个类的距离定义为最近元素之间的距离，并且逐渐选择比较靠近的类聚集，不断进行选择，直到满足终止条件。NNFA算法的基本思路是临近点的属性相同。如果在计算中最近的两点距离小于阈值，就将它们归结为一类。当某一个聚类所包含的元素大于数量的阈值，该数据类型被定义为真正的聚类。

NNAF聚类算法中把一个点作为一类，然后把这一点的所有邻点和新加入的邻点全部归结为已归类点，然后在对未归类点进行聚类，具体算法如下：

输入点集W={c1,c2,c3,c4,……,cn,cn+1},规定距离阈值为d，数量阈值为q。

输出每一个点的属性值。

For(i=1;n;i++)

使用sun算法找到Ei最近邻点之间的距离，并在其中邻点的属性集合中加入Ei。

建立点Ei的属性集

j=1;

Point=null

While(w,null)do

找到W中的任何一个点h，将h指向point，并将h从W集合中删除，重复操作。

如果point赋值的相邻点存在属性值为空的点，将加入堆栈的点的属性值归为j，并且将j点从W中删除。栈顶点的最邻近点和以之为最邻点的点为类近邻点。

当数据密度和类的间距分布不均匀的时候就会出现阈值设定不准确的问题，同时也会丢失最邻近点的选择，从而不太适用于所在类的进一步扩展。阈值选定的错误，很有可能将距离较近且密度较大的几个类划分为同一类，因此基于上述的问题，进一步提出了数据分区的临近类算法，PNNAF算法。

2. PNNAF算法分析。

1)数据分区。在整个数据空间中，采用数据统计分布特性来进行数据区分，首先需要对数据库取样，对数据分布的特性进行统计，然后分析其统计结果，确保每一个划分区域的数据密度能够均匀分布。

2)局部聚类。NNFA的算法是局部聚类，在计算的过程中需要记录在合并阶段用到的信息，保证划分的距离不能大于阈值d。

3)PNNAF的算法。输入集合W={c1,c2,c3,c4,……,cn}，分区的个数为s

输出每一个点及邻点的属性值。

For(i=1;nc；i++)

利用NNAF的算法计算出每一个属性值，并记录可能在合并阶段用到的类的代表点及边界点

For(j=1;s;j++)

将classA B分为两个相邻的区域PA、PB，PA、PB满足条件，进行A、B类的合并，形成一个新类C。通过计算可以发现，PNNAF的算法能够有效解决NNAF中的弊端，实现分布均匀等问题，并且可以以任意形态进行数据聚类分析。

1.4 k-means聚类算法的改进分析

k-means聚类算法属于聚类分析中一种比较常见和广泛的划分算法。k-means是基于原型的聚类算法，制定类别数为K，对样本数据进行集合聚类。聚类的结果会通过各聚类中心来表达。算法采用迭代更新的方法，每一次迭代的过程函数值都在减小，去函数最小值，达到最优的聚类结果。

1.改进k-means算法。 改进k-means算法的基本思路可以分为两部分。第一部分从聚类的样本中选取种群，然后执行传统算法，第二部分在完成传统算法后产生新的数据种群进行k-means操作。这两部分是相互循环进行计算，通过计算选择聚类问题的最优解。具体的改进从以下四个方面进行：

第一，利用浮点编码进行聚类数据编码，这样可以简化编码的整个过程，运算速度也会有效提升；

第二，保证每一个数据个体不被算法破坏，改进算法采用了轮盘和最优保存的方式相结合；

第三，通过交叉算法减少无关联数据产生，需要根据上文提到的算法进行近邻匹配，提高k-means算法局部搜索的能力；

第四，提高k-means算法局部的搜索速度，在传统算法结束后，进行下一个数据群的k-means优化。

2.改进k-means算法流程。改进k-means算法也是随机产生的一个群体进行最优数据搜索的整个过程，与传统算法的区别是，在遗传操作之后，需要对每一个数据进行k-means优化，然后将优化结果作为下一个数据集。反复迭代操作，寻求最佳结果。具体的改进k-means流程如下：

1)对计算参数进行设置，样本数据集M，聚类数值为H，迭代次数最大为Z，概率计算为P；

2)种群初始化，在样本中选取N个点作为聚类中心，并且进行编码，迭代次数为Fsize；

3.对数据群的个体进行计算，计算出相对应的适应度；

4.对数据个体进行交叉计算；

5.交叉计算后得出的个体进行变异计算，产生新的数据集；

6.新种群中每一个数据个体进行k-means操作，不断迭代计算，计算出最优值，判断结果条件，若是满足输出结果，若是不满足，重新按照步骤操作。

3.编码方法。 按照k-means算法运行的整个流程，首先要对数据集群进行编码和运算。编码有两种方式，一种是染色体编码，另一种是浮点编码。本文以浮点编码为主要编码方式。所谓的浮点编码，就是把染色点看成一个由M个数据集组成的数据串。对C维样本数据的M类聚类算法，在聚类算法中染色结构可以分为：

Y={p15,p16,p17,……p1d,p30,p31,p32……pkd}每一条染色体的长度为K*D的浮点码。

4. k-means的优化算法。 k-means具备非常强的搜索能力，k-means是在传统算法结束后引入k-means算法，对每一个数据集进行k-means操作与优化，为新的数据集做准备，这样可以很大程度上提高局部的搜索能力。

1)根据k-means计算产生的新的数据种群进行聚类编码，对样本进行划分，然后计算出分类矩阵W；

2)对W矩阵新的聚类中心进行编码；

3)为新的聚类中心重新计算适应度，找出最不合适的值，进行替换，开始新的计算操作。

2 聚类算法的应用与仿真

为了验证k-means聚类算法的有效性，本文在一定环境下进行了仿真实验。

2.1 评分确定

以某高校学院经费绩效评价为例，抽取高校中的40位各科研室的教授，向他们发放问卷，请他们给出经费评价体系中1-3层的评价，首先得出的是财务指标，成果指标及合适指标，用U1、U2、 U3来表示，分别是0.44、0.11、0.67。根据同样理论得出第二层和第三层的指标权重。在实验中采用百分比来计算总分，根据测算出的每层权重比例，将100分赋值到各个指标中，邀请15位高校专家对高校经费按照评价指标体系分解的指标值进行打分汇总至一级指标，如表1所示。

表1

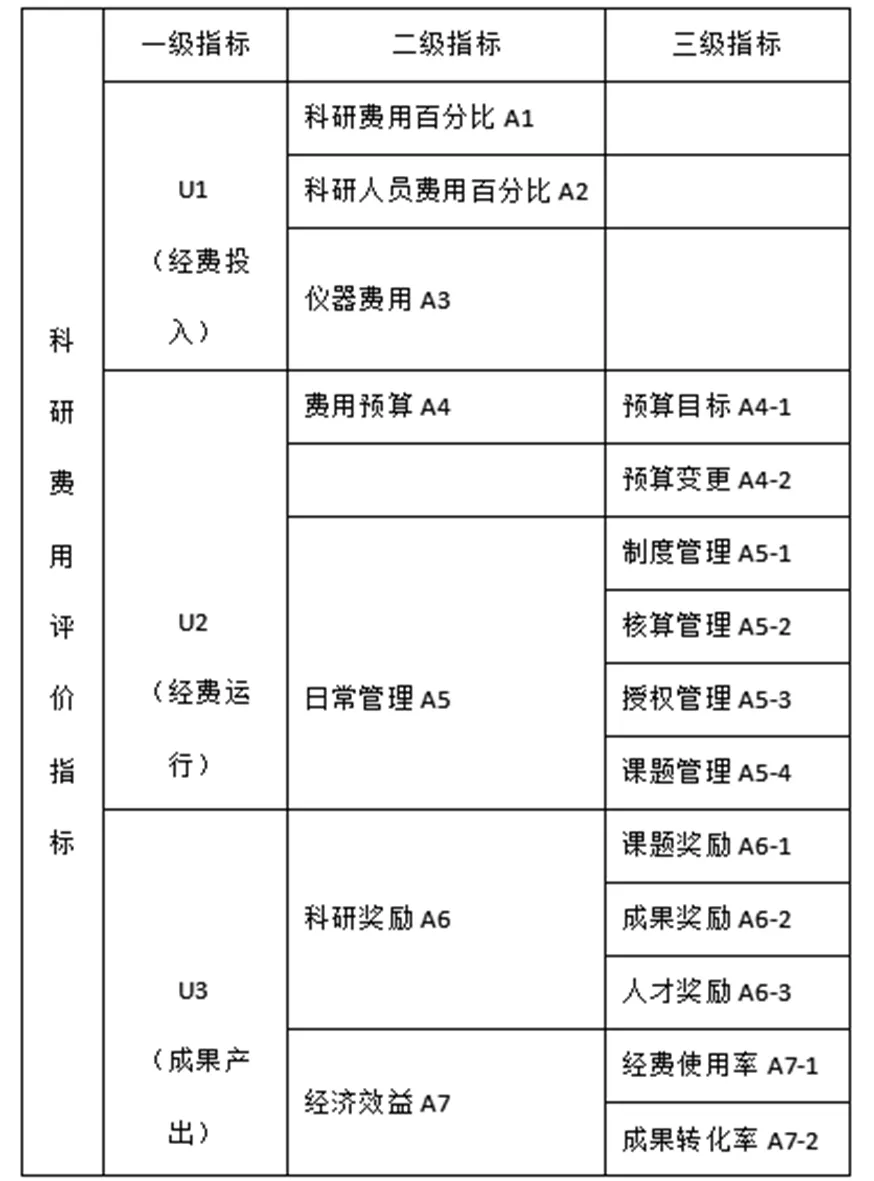
2.2 聚类分析

根据学科情况考虑该高校实际经费的使用情况，将聚类分析分成3类，本文使用Matlab系统聚类方法对经费使用问题进行处理。处理结果中，15个学院全部进入到聚类中，当变量系统聚类分析成3类时，处理情况如表2所示。通过聚类算法分析转化成可视化图谱展现给用户，显示出个学院的科研部门的经费投入与成果产出等情况。

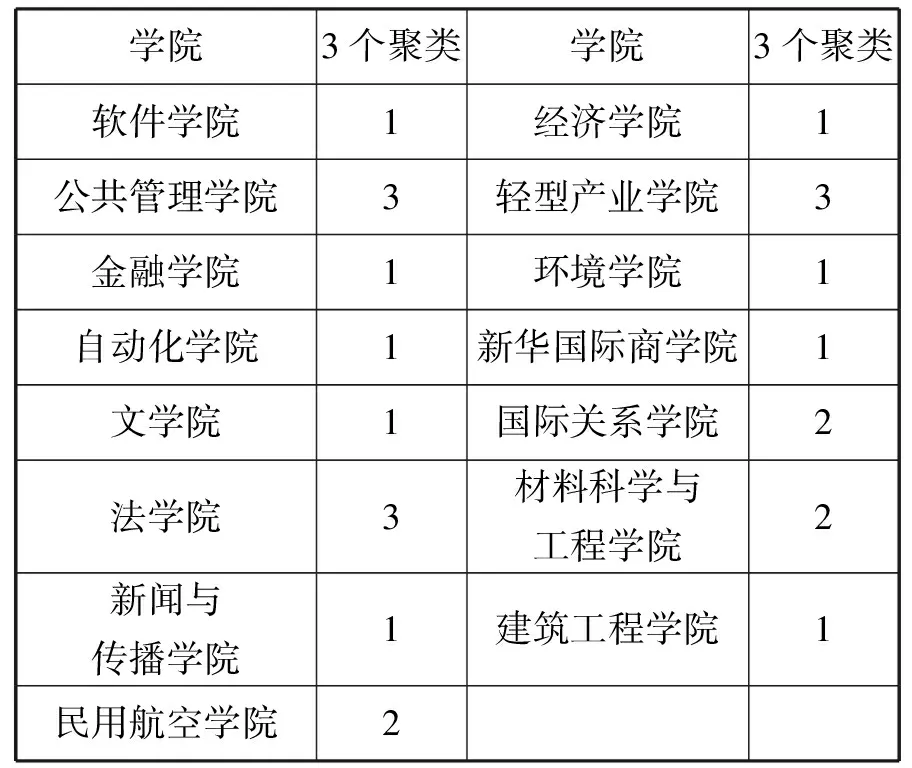
表2 聚类成员

通过对表2和图4的分析可知，学院经费评价中，科研成果的得分比较高，如金融学院、自动化学院、经济学院、环境学院，此类学院的学术论文、课题研发、专利成果收获颇丰。无论是成果还是队伍建设比较完整，在成果与应用的转化过程中效果显著。经费支出中购买仪器设备、业务费用及人员费用的所占比例科学，但需要加强对预算的管理，经费转拨的管理；2类学院如国际关系学院、材料科学工程学院的科研经费评价中，科研成果得分居中，但队伍建设良好，科研成果转换与成果奖励比较弱，这样的情况也受到学科性质的影响；3类学院中公共管理学院、轻型产业学院、法学院的科研绩效评分中，科研产出比较低，成果较低，论文级别与课题研究比较低，队伍建设不够完善，需要加强团队建设，鼓励教师之间互相交流与合作。

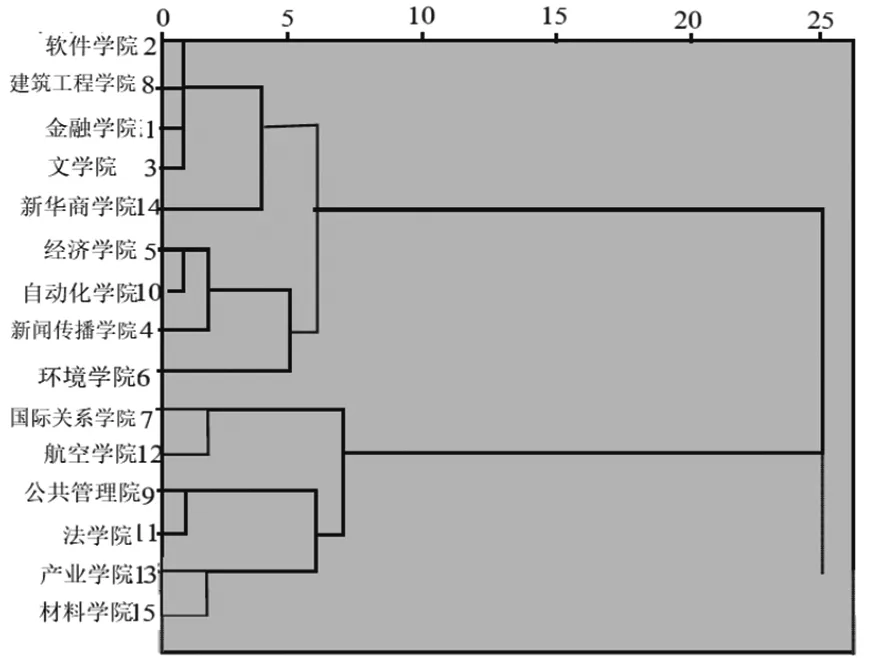
图4 聚类算法谱系图

3 结束语

聚类分析在数据挖掘中是一个应用非常广泛的活跃领域，并且在整个算法中包括很多方法，包括层次法、密度法或基于网格等方法，每一种算法都有其自身的特点。本文就数据挖掘聚类算法中的NNAF和PNNAF算法，对使用中的优势和劣势进行详细的分析。并对数据挖掘系统的聚类分析进行仿真实验，在实际的应用可以根据聚类的对象与属性选择合适的聚类方法，并适当加以改进，保证最佳的聚类质量，跟上时代发展的步伐，聚类算法将会在数据挖掘领域获得重大的发展。