Banach空间中不适定线性算子的广义概率范数
2019-11-13江慧敏
江慧敏
(皖南医学院,安徽 芜湖 241000)
0 引言
随着非线性动力学控制的发展,采用应用数学和控制学,进行动力学控制优化,提高动力学控制系统的输出稳定性,Banach空间中不适定线性算子是非线性动力学控制系统的中枢单元,通过构建Banach空间中不适定线性算子的广义概率范数解,采用稳定约束泛函方法,进行Banach空间中不适定线性算子的稳定性特征分析,构建Banach空间中不适定线性算子的概率范数分布模型;结合差分方程构建方法,进行广义范数的动力学特征建模,提高系统的输出稳定性[1]。研究Banach空间中不适定线性算子的广义概率范数求解方法,在数学力学与控制等领域中具有重要意义[2],相关的数学分析方法研究受到重视,构建概率拟合模型,实现Banach空间中不适定线性系统的稳定性特征分析;结合正态分布模型、正态对数分布模型和Weibull分布模型,实现对Banach空间中不适定线性算子的广义概率范数分析,并进行数学推导和证明,得出有效性结论。
1 模型构造及相关定理
1.1 Banach空间中不适定概率拟合模型
为了实现Banach空间中不适定线性算子的广义概率范数分析,在给定的扰动初始条件下,构建Banach空间中不适定概率拟合模型,分析Banach空间中不适定线性算子的广义概率范数,构建概率拟合模型实现Banach空间中不适定稳定特征分析。Banach空间中不适定线性特征点为(t,f),采用线性无关积分控制方法[3],得到广义特征正则约束项为φ(t′,f′)Wz(t-t′,f-f′),采用非线性KdV-KSV方程进行Banach空间中不适定线性算子的模糊约束解分析,稳定特征解f可以看作是在(t,f)的邻近点(t-t′,f-f′)上的加权,求解Banach空间中不适定线性算子的稳定核,得到第i个解空间向量的调控函数。在Banach空间中不适定线性算子多项式核取q=4,边值解向量bk取作b2=b-2=1,b1=b-1=2,b0=0。
在扰动特征泛函下分析Banach空间中不适定线性算子的特征解,并进行模糊调度,得到Banach空间中不适定线性方程满足:
(1)
对任意Banach空间中不适定线性算子,采用变分结构调节方法,得到惯性常量ρj-、ρj+,构建随机泛函微分方程gi(·)。对于一个独立随机分布凸组合函数,当广义概率密度特征解α,β∈R,且α≠β满足,
(2)
注意到正态分布具有无偏性,得到Ψ1(d1(t))是矩阵K(z1+z2+z3)-1KT,WZ1-1WT和L(Z2+Z3)-1LT在d1(t)(0≤d1(t)≤h1)上的凸组合,定义尺度参数:
(3)
且
∑=diag{max{|ρ1+|,|ρ1-|},…,max{|ρn+|,|ρn-|}}=diag{p1,…,pn}
(4)
∑1=diag{ρ1+ρ1-,…,ρn+ρn-}
(5)
由于一个多项式的阶次相对于原点是不变的,所以不失一般性n可以取作0,构建Lyapunov泛函,则上式可以简化为:
(6)
此时Banach空间中不适定概率拟合的确定系数ck,约束条件为ck=-c-k。
定理1 若取Banach空间中不适定概率特征量为q=4,b2=b-2=1,b1=b-1=2,b0=0,采用Bochner-Riesz矩阵构造Banach空间中不适定概率分布矩阵,由正态分布模型和正态对数分布模型,得到模糊相关性系数ak,则有:
a0[1-1+2-2]=0×a0
a1[c2-c-2+2c1-2c-1]=1×a1
(7)
采用非线性方程进行特征解分析,得到在齐次Sobolev空间中,广义极值分布系数c1=-c-1,c2=-c-2,采用变尺度融合方法,构建Banach空间中不适定线性算子的范数融合模型,提高输出稳定性和自适应性[4]。
1.2 Banach空间中不适定线性算子广义极值分布
采用Lyapunov-Krasovskii差分进化方法进行Banach空间中不适定线性算子的输出稳定特征解分析,构建Banach空间中不适定线性系统分析模型[5],求解不适定线性算子的组合模型对称解,令:
(8)
假设{qN}单调递增,qN≥1,而且当N→∞时,得到qN→∞,得到Banach空间中不适定线性算子的拟合特征泛函为:
(9)
当Dn≤FK-S(K-S检验分位值)时,样本控制函数满足:
x(t)=φ(t)t∈[-h,0]
(10)
其中x(t)=[x1(t),x2(t),…,xt(t)]T是Banach空间中不适定概率拟合的状态向量,求解边值解,得到Ψ1(d1(t))是矩阵K(Z1+Z2+Z3)-1KT和矩阵WZ1-1WT的拟合优度检验组合,Ψ2(d2(t))表示为矩阵L(Z2+Z3)-1LT与MT(Z2+Z3)-1MT的双曲泛函,当Ψ1(d1(t),d2(t))<0,Banach空间中不适定概率分布的特征解满足:
f(x1,x2,i)-g(y1,y2,i)
(11) 其中,∀x1,x2,y1,y2∈R,设x*是Banach空间中不适定概率密度解集{xk}中的一个极限点,采用χ2检验法,进行Banach空间中不适定线性算子广义极值分布模型设计,在P0(x10,x20)点将f(x1,x2)和g(x1,x2)作级数展开分析,结合差分进化方法进行线性模拟[6],得到近似线性方程: (12) 综上分析,构建Banach空间中不适定线性算子正定最小特征为: (13) 如果C0(x*)=0,则: Y(P,Q,β)=Y[red(P,Q,β),Q,β] (14) 构建Banach空间中不适定线性系统的定量递归分析模型,采用约束控制方法进行广义概率范数量化特征分析,假设f(x),f(x,q)在X上的值域上的任意初始矩阵,不适定线性算子概率范数表示为f(X),f(X,q),因为F(X)是f(X)的唯一极小范数特征解,因此,存在非负周期函数: (15) 在延迟反馈控制下,进行扰动特征泛函[7],构建不适定线性算子概率范数的线性方程组,因为: (16) 在信息扩散分布模型中,构建约束变量,可得: (17) 因为Banach空间中不适定线性算子lnx,ex均为单调递增函数,所以: (18) 采用K-S检验法、χ2检验法和AD校验法分别对不同概率分布模型所拟合的曲线进行特征拟合[8],得到最小特征为: (19) 如果C0(x*)=0,则: Y(P,Q,β)=Y[red(P,Q,β),Q,β,] (20) Banach空间中不适定线性系统的广义概率范数求解问题等价于求函数F(x,q)的f(x,q)的区间扩张问题,结合不适定线性算子概率范数分布式解析方法,进行概率密度泛函。在此基础上,进行稳定性和收敛性证明[9]。 证明:结合二次非线性波动演化博弈方法实现对不适定线性算子的广义概率稳定特征解自适应寻优,根据正态分布模型、正态对数分布模型和Weibull分布模型,进行输出稳定性调节,当满足: (21) (22) δ·p1-2p2+ρ2A2-δρ1A1+c2+cr=0 (23) ρ2(p2-c2-cr)-δ·(1-δ)μ2A2=0 (24) δ·p1-2p2+ρ2A2-δρ1A1+c2+cr=0 (25) ρ2(p2-c2-cr)-δ·(1-δ)μ2A2=0 (26) (27) 设 (28) 采用相关系数检验法(PPCC)实现稳定性判断,实现对Banach空间中不适定线性算子的广义概率范数分析,输出为: (29) 根据Lyapunov稳定性原理,得到Banach空间中不适定线性算子的广义概率范数是稳定收敛的。 构建概率拟合模型,实现Banach空间中不适定线性系统的稳定性特征分析;在给定的约束泛函下,采用Lyapunov-Krasovskii差分进化方法进行Banach空间中不适定线性算子的输出稳定特征解分析;采用K-S检验法、χ2检验法和AD校验法分别对不同概率分布模型所拟合的曲线进行特征拟合;采用约束控制方法进行广义概率范数量化特征分析,结合由正态分布模型、正态对数分布模型和Weibull分布模型,实现对Banach空间中不适定线性算子的广义概率范数分析,提高输出稳定性。分析得知,Banach空间中不适定线性算子具有稳定解,广义概率范数是稳态收敛的,研究结论在非线性控制领域具有很好的应用价值。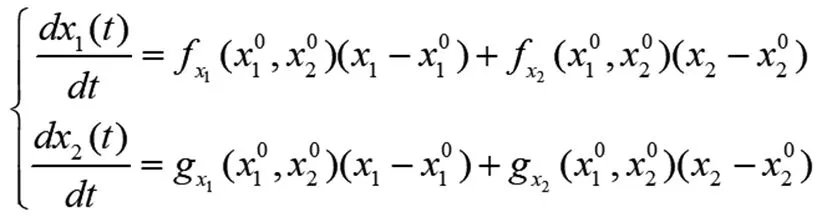
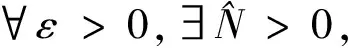
2 不适定线性算子概率范数分析及证明
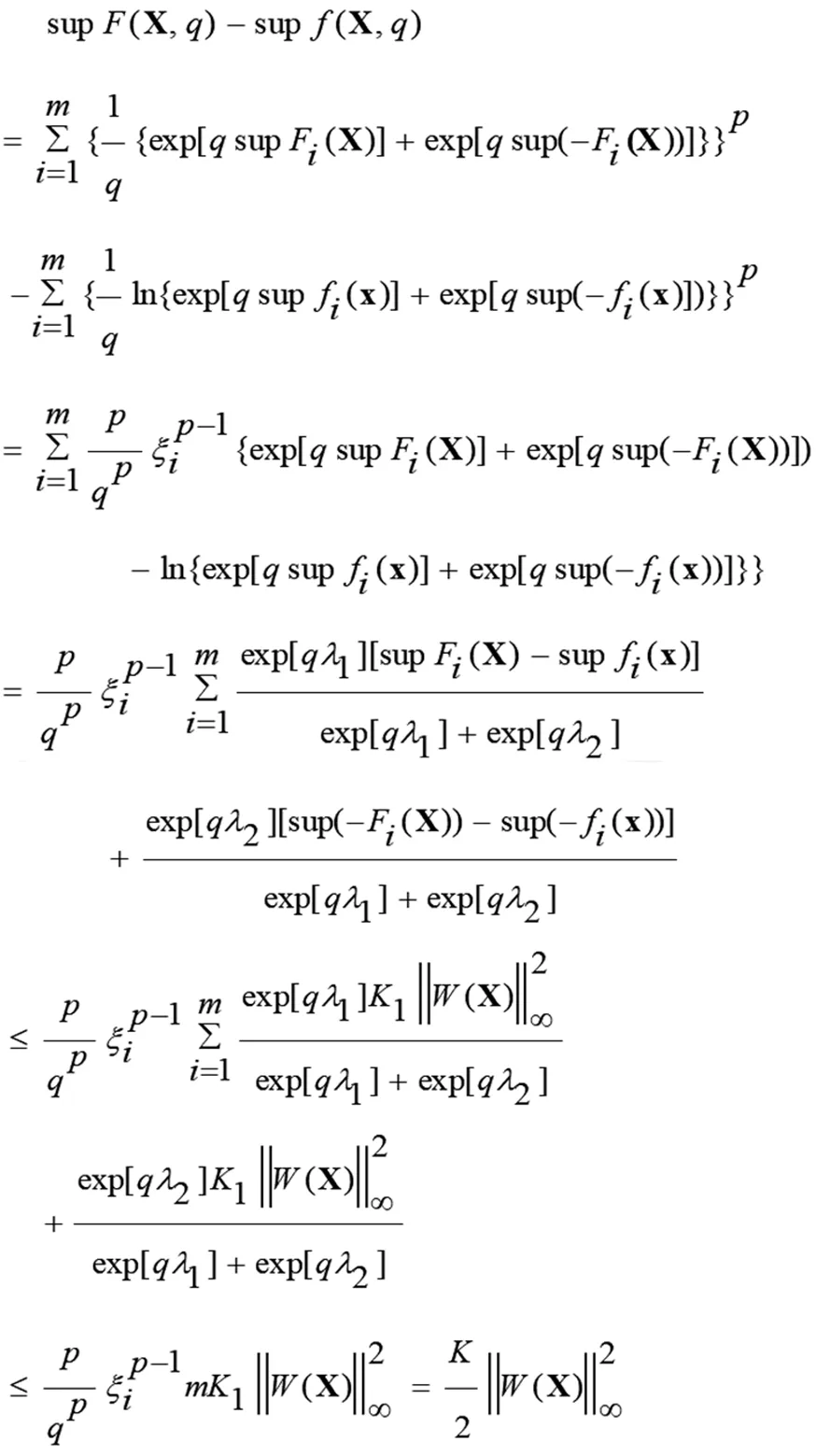
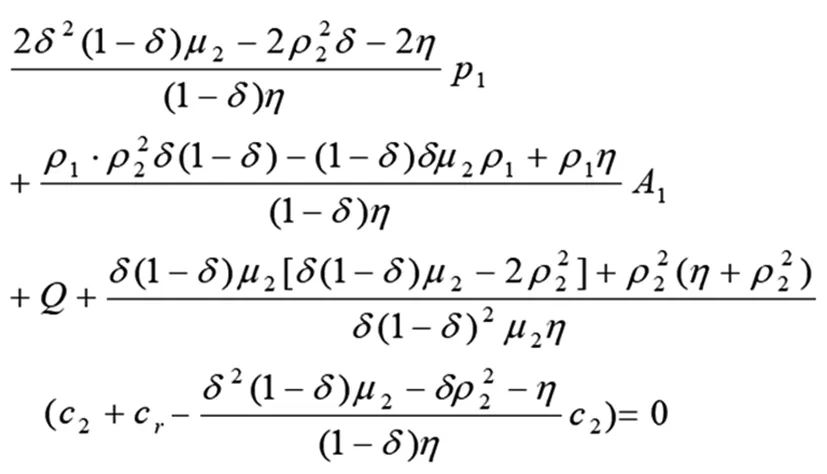
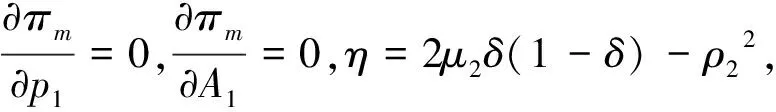
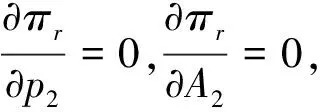
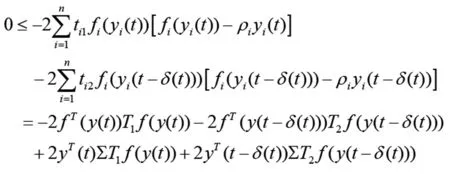
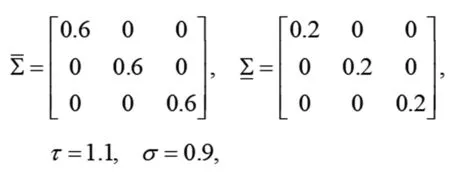
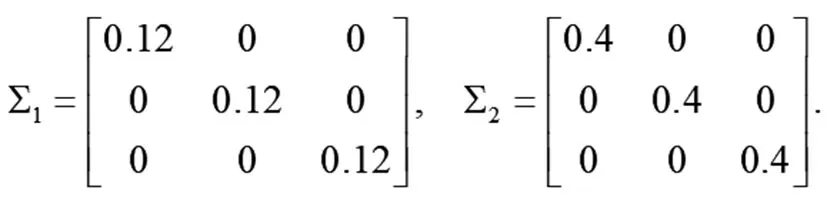
3 结语
