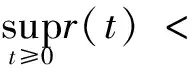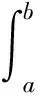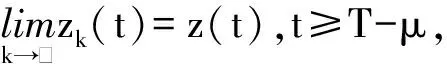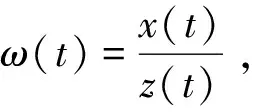奇数阶带分布时滞微分方程最终正解的存在性

赵环环,刘有军

(山西大同大学 数学与统计学院, 山西 大同 037009)

近年来,高阶中立型微分方程与其所对应的不等式最终有界正解的存在性受到了许多学者的关注,得到了一些较好的研究成果。2004年,欧阳自根等[1]研究了奇数阶中立性微分方程

和相对应的不等式

得到了它们存在最终正解的充要条件。

2013年,刘有军等[2]研究了偶数阶带分布时滞微分方程

和相对应的不等式

得到了它们存在最终正解的充要条件(这里n为偶数)。

从上述方程的不断发展过程和其证明过程可以看出,学者们对这类方程讨论时,将方程的阶数分奇偶来分别讨论,并且在证明过程中所用的方法差异很大,本文通过对文献[1-2]认真研读和详细分析后,将方程的阶数由偶数改为奇数,利用新的引理,克服了在算子构造上的困难,同样得到了它们最终正解存在的充要条件。为了相关工作,还认真查阅了关于非振动解存在性的著作和论文，如文献[3-8]。

本文考虑奇数阶带分布时滞微分方程

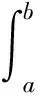
(1)

和相对应的不等式

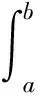
(2)

(1)这里n=2k+1,k≥1是一个正整数, 0

(2)r∈C([t0,),R+),r(t)>0,p∈C([t0,)×[a,b],R+),q∈C([t0,)×[c,d],R+);

(3)f(u)是关于u的单调不减的实函数, 且有uf(u)>0。

定义1若方程(1)的一个解有任意大的零点,则称其为方程(1)的振动解；否则,称之为非振动解。

定义2 若x(t)是方程(1)的解, 且存在充分大的T>t0,当t≥T时,x(t)≥0,则x(t)为方程(1)的一个最终正解。

(3)

证明本引理的证明过程和文献[2]中引理1的证明十分相似,在这里不再赘述。证毕。

定理1设引理1的所有条件都成立, 且满足条件(H)p(t,r)+q(t,σ)>0, 对充分大的t, 则方程(1)存在最终有界正解的充要条件是不等式(2)存在最终有界正解。

对(2)式从t到积分, 得y(n-1)()用(3)式, 有重复以上步骤n-1次, 再用到(3)式, 可得

用Toneelli's定理,交换积分次序, 得

即

(4)

选取T≥0, 使得(3)式成立, 且x(t-u)>0,t≥T。下面考虑函数集

Ω={z∈C([T-μ,),R+):0≤z(t)≤1,t≥T-μ}

且定义Ω上的算子S如下:

易知S是连续的。 由(4)式容易看出S是从Ω到Ω的一个映射, 对于任意的z∈Ω,都有(Sz)(t)>0,T-μ≤t

所以ω(t)≥0,t≥T是(1)式的一个非负解。

下面证明ω(t)>0,t≥T-μ, 否则设存在t*≥T, 使得ω(t)>0,T-μ≤t≤t*, 且ω(t*)=0。则

这暗含着p(t*,r)≡0,q(s,σ)f(ω(s-σ))≡0,这与(H)矛盾。 因此ω(t)是方程(1)的一个最终有界正解, 证毕。