基于SVM模型的充填体强度与采场稳定性需求智能匹配研究
2019-11-13白春红
白春红
(阜新高等专科学校计算机与信息工程系,辽宁 阜新 123000)
0 引 言
随着我国越来越多的矿山进入深部开采,地压问题已是深部开采过程中无法回避的安全问题,现阶段控制深部开采地压问题的最有效方法为充填采空区[1-2]。在空场嗣后充填采矿法中,一步骤回采矿房,二步骤回采矿柱,一步骤回采结束后即进行充填,保障二步骤回采矿柱时的采场稳定。充填体的强度设计十分关键,选择合理的充填体强度,既要能保障采场的稳定性,又要节约水泥用量,降低充填成本[3-4]。采场充填体强度受多重因素的综合影响,各因素之间相互影响极为复杂[5]。现阶段关于充填体强度的确定主要依赖于现场经验、经验公式、设计手册等,采用上述方法确定的充填体强度往往不是最佳的充填体强度。关于充填体强度与采场稳定性之间的智能需求匹配研究方面,常庆粮等[6]采用BP神经网络模型对膏体充填材料的配比进行了研究,结果表明采用BP神经网络法预测充填体配比是可行的。支持向量机(SVM)是Vapnik1995年提出的一种机器学习方法[7],该方法对于高纬度非线性问题具有很好的学习能力。赵洪波等[8]采用SVM方法对露天边坡的稳定性进行了预测研究;崔海霞[9]采用SVM方法对混凝土的强度进行了预测研究;李素蓉[10]采用SVM法对矿山岩爆进行了预测研究。上述研究表明,SVM对于小样本机器学习具有较好的预测效果,本文以矿山充填体强度预测为目标,采用SVM建立充填体强度预测模型,探索一种充填体强度与采场稳定性需求的智能匹配方法。
1 支持向量机(SVM)基本原理
支持向量机(SVM)是基于统计学理论和结构风险最小化原则提出的一种方法,该方法通过内积核函数进行非线性变换,能够在复杂数据之间进行学习、训练。
定义样本数据集(xi,yi),i=1,2…,n,xi∈Rn,yi∈R。采用线型回归函数f(x)=ax+b对样本数据进行线型拟合,假设所有的样本数据均可在误差为ε的范围内进行线型函数拟合,计算见式(1)。
‖yi-(ax+b)‖≤ε,i=1,2,…,k
(1)
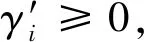
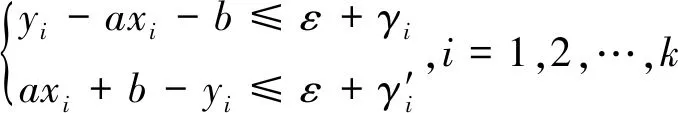
(2)
优化目标为‖ω‖2/2,将两个修正因子引入优化目标,可得式(3)。
(3)
式中,C为常数,代表超出误差ε时的惩罚度。
引入Lagrange函数进行处理式(2)和式(3),可得式(4)和式(5)。
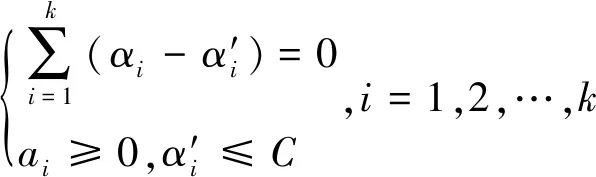
(4)
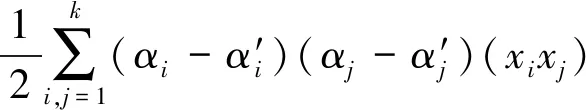
(5)
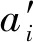
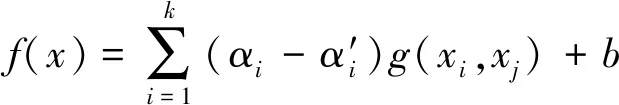
(6)
2 基于SVM充填体强度预测模型的建立
2.1 充填体强度选择的影响因素
矿体充填体强度的选择需要考虑多方面因素后综合确定,充填体强度的选择要综合矿体赋存条件、采矿方法、围岩稳定性、充填体材料、暴露面积等综合确定,通常在做设计时,在选择充填体强度时,每个矿山设计一个充填体强度,而实际生产中,每个采场的条件都不同,所需要的充填体强度也不同,充填体的强度并未因采场条件的变化而变化,可能会出现采场因充填体强度不足发生垮塌或因充填体强度过高而造成浪费。为确定合理准确的充填体强度,综合考虑,最终选择了矿体的埋深深度(X1)、矿体厚度(X2)、矿体长度(X3)、尾砂粒径不均匀系数(X4)、f系数(X5)、可靠性指标(X6)、一次充填高度(X7)、采场暴露面积(X8)8个因素作为充填体强度选择的影响因素。其中,f系数(X5)为岩石坚固性系数,是由围岩单轴抗压强度(MPa)与10的比值。可靠性指标(X6)=实际充填体强度值/理论最低充填体强度值,这里的实际充填体强度值是通过查阅相关文献、设计资料、询问矿山技术人员等获得,理论最低充填体强度值是根据其他参数建立的数值模拟模型并通过模拟计算出的最小充填体强度值。
2.2 样本数据及标准化处理
通过调查国内外百余座矿山的矿体赋存条件和充填强度值,最终选取了78组数据作为本次研究的样本数据,其中70组数据作为训练样本,其余8组数据作为预测样本,限于篇幅部分数据见表1。从表1中可以看出,8个影响因素数据大小差别较大,直接采用这些数据可能造成计算结果不收敛,为了使数据之间具有相比性,对所有数据进行归一化处理,计算见式(7)。
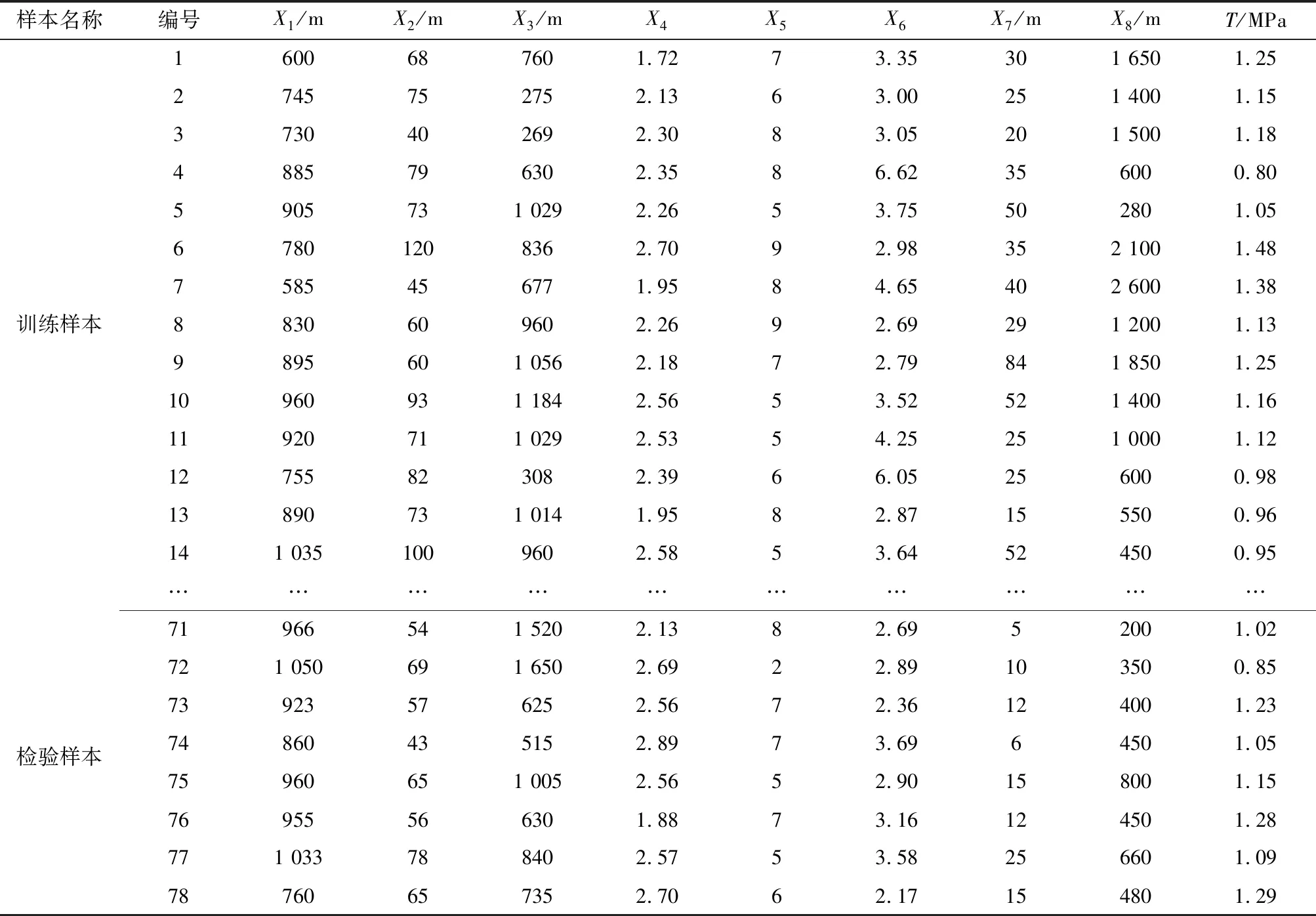
表1 部分样本数据
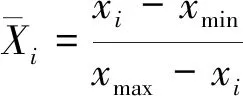
(7)
2.3 核函数及参数选择
核函数对于预测结果影响显著,选择合适的核函数是建立正确预测模型的基础。采用SVM法对充填体设计强度进行预测,选取了X1、X2、…、X8等8个条件属性,而训练样本数为70,远大于条件属性个数,选定RBF核函数预测精度较高,比较适合本次预测模型,RBF核函数见式(8)。
K(x,xi)=exp{-|x-xi|2/σ2}
(8)
采用核函数RBF时,惩罚因子C与核函数g对模型预测精度的影响非常大,其中惩罚因子C是影响模型平滑度与训练时间的重要参数,而核函数g控制了模型的拟合程度好坏。选择合适的惩罚因子C与核函数g对模型预测结果的准确性至关重要,本次采用网格搜索法确定最优的参数组合(C,g)。采用Matlab程序编程,首先对参数C、g进行初步粗选,根据初选结果再进行精选,最终确定最优的参数组合(C,g)=(1,0.707)。
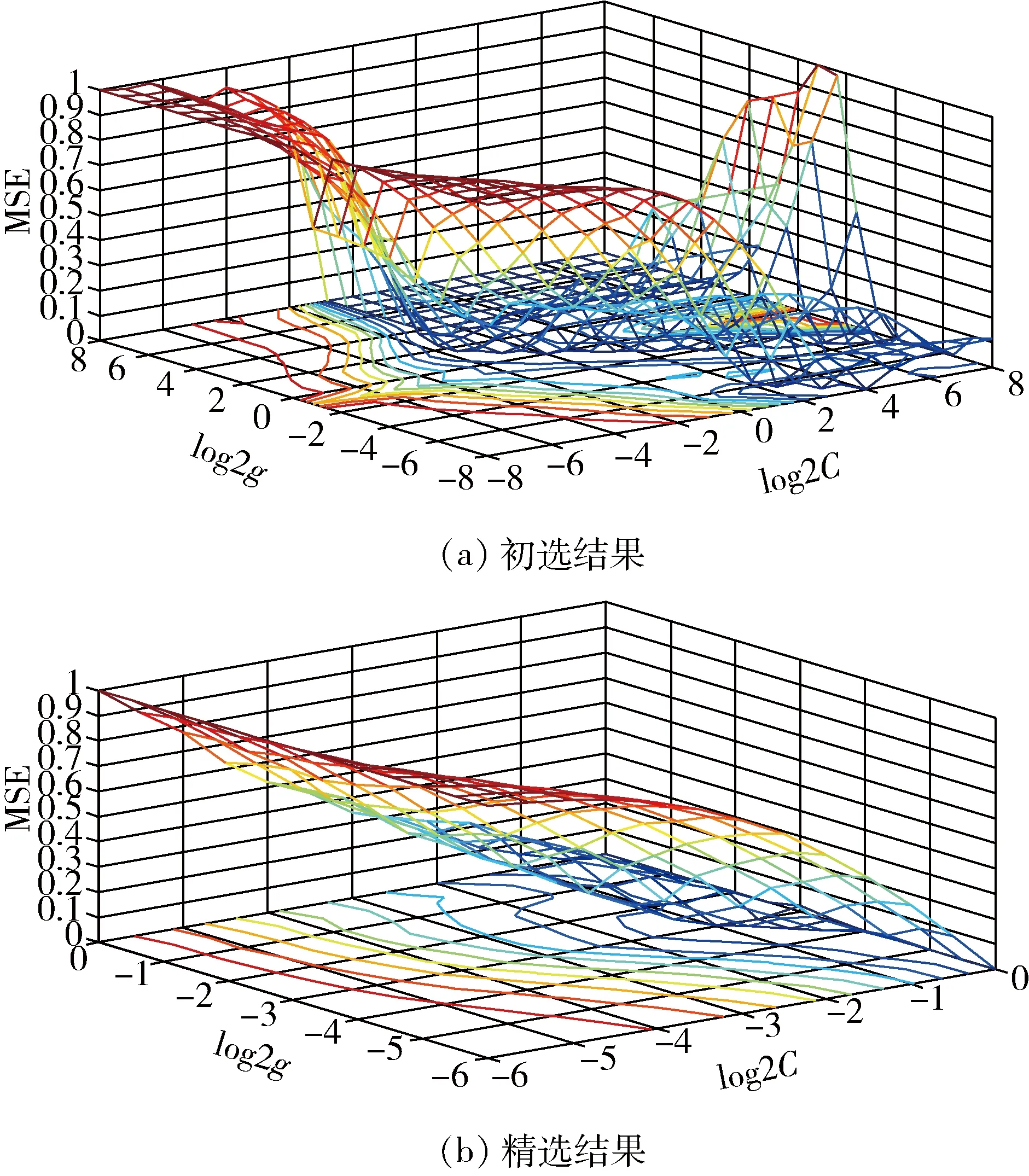
图1 最佳核函数参数Fig.1 Optimal kernel function parameters
2.4 数据仿真及误差分析
将确定的最优的参数组合(C,g)=(1,0.707)输入SVM模型中,为了对SVM模型的预测结果进行评价,将BP人工神经网络与SVM模型预测数据进行对比,图2为SVM充填体强度预测模型的预测结果与样本数据的比较,图3为BP神经网络模型的预测结果与样本数据的比较,表2为SVM与BP模型预测误差比较。从表2中可以看出,SVM模型预测结果与样本数据的最大误差、最小误差和平均误差均优于BP神经网络模型。
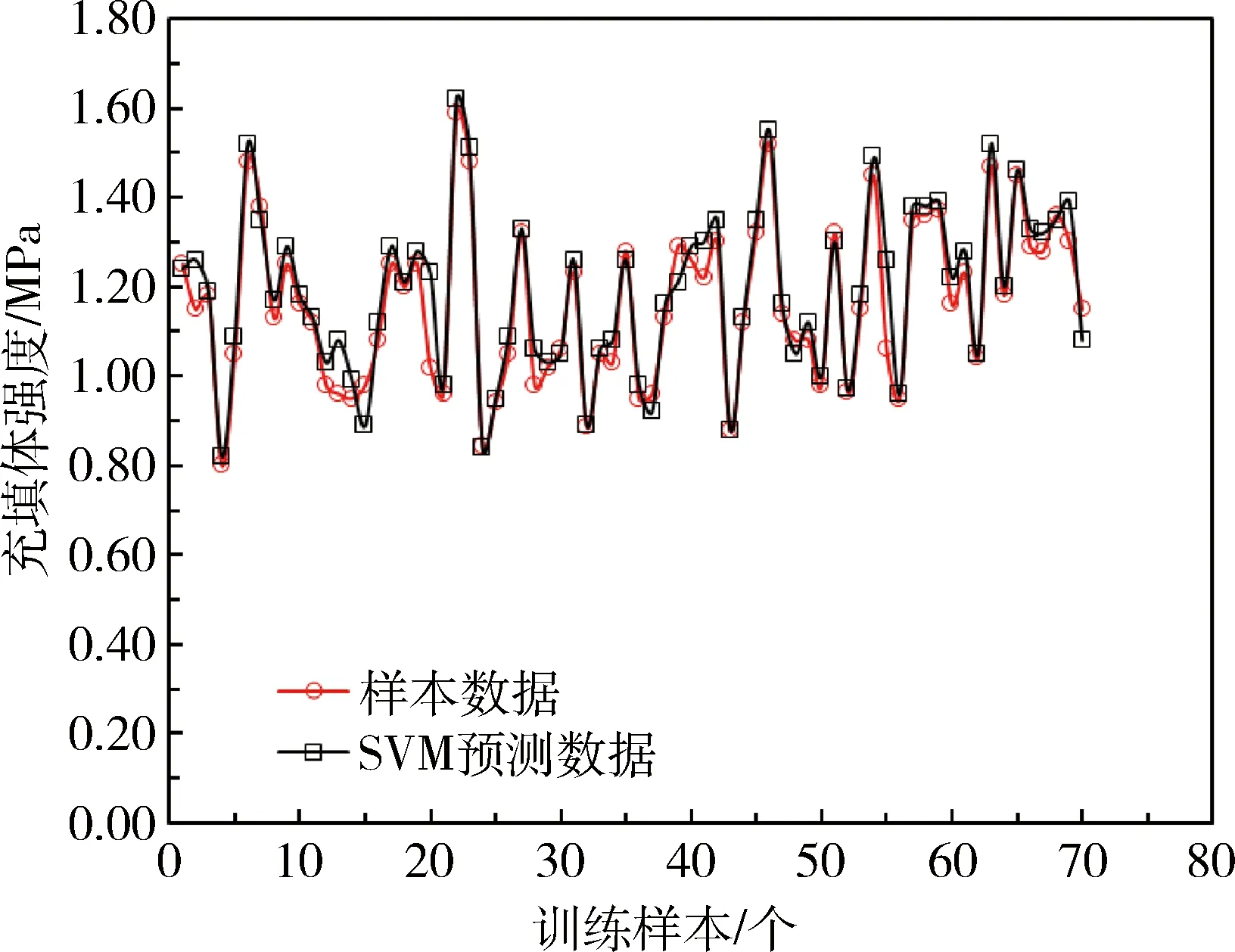
图2 样本数据与SVM预测数据对比Fig.2 Comparison of sample data and SVM prediction data
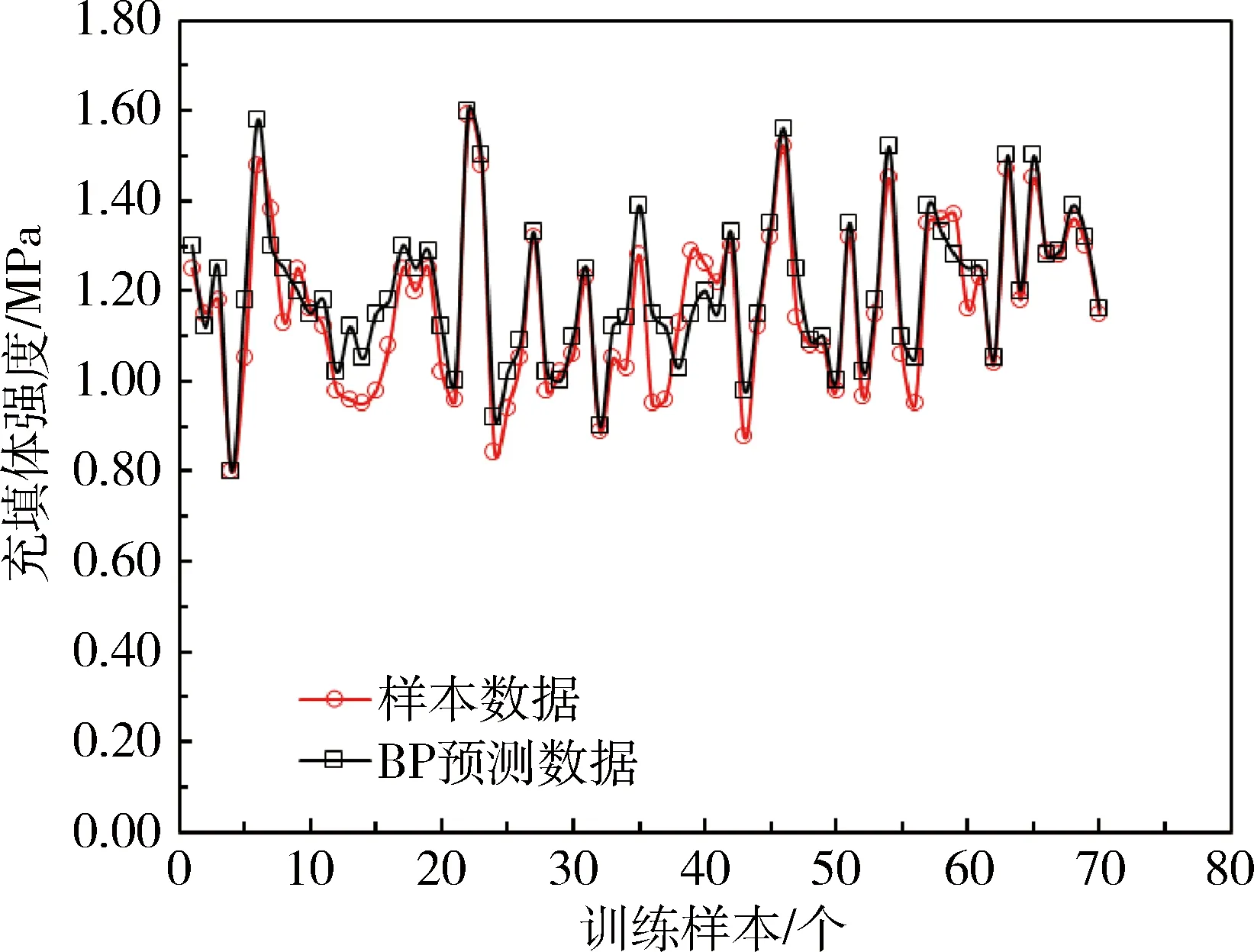
图3 样本数据与BP预测数据对比Fig.3 Comparison of sample data and BP prediction data
表2 SVM与BP模型预测误差比较
Table 2 Comparison of SVM model and BP model prediction errors

模型最大误差/%最小误差/%平均误差/%BP10.982.587.01SVM3.520.082.41
2.5 模型检验
将检验样本的数据输入建立好的SVM充填体强度预测模型中进行预测,预测结果见图4。从图4中可以看出,预测值与检验样本原始值的最大误差为3.51%,最小误差为0%,平均误差为1.28%,预测误差非常小,精度高,具有一定的优越性和实用性。
针对充填体强度设计问题,采用SVM预测模型在较少的实际样本数据的情况下获得较高的预测精度,充分体现了SVM预测方法的优越性。将矿体的埋深深度(X1)、矿体厚度(X2)、矿体长度(X3)、尾砂粒径不均匀系数(X4)、f系数(X5)、可靠性指标(X6)、一次充填高度(X7)、采场暴露面积(X8)作为预测模型的条件属性,将充填体强度作为决策属性,采用参数组合(C,g)=(1,0.707)得到的模型预测精度高,因此,将该模型作为矿山强度匹配模型确定充填体强度。
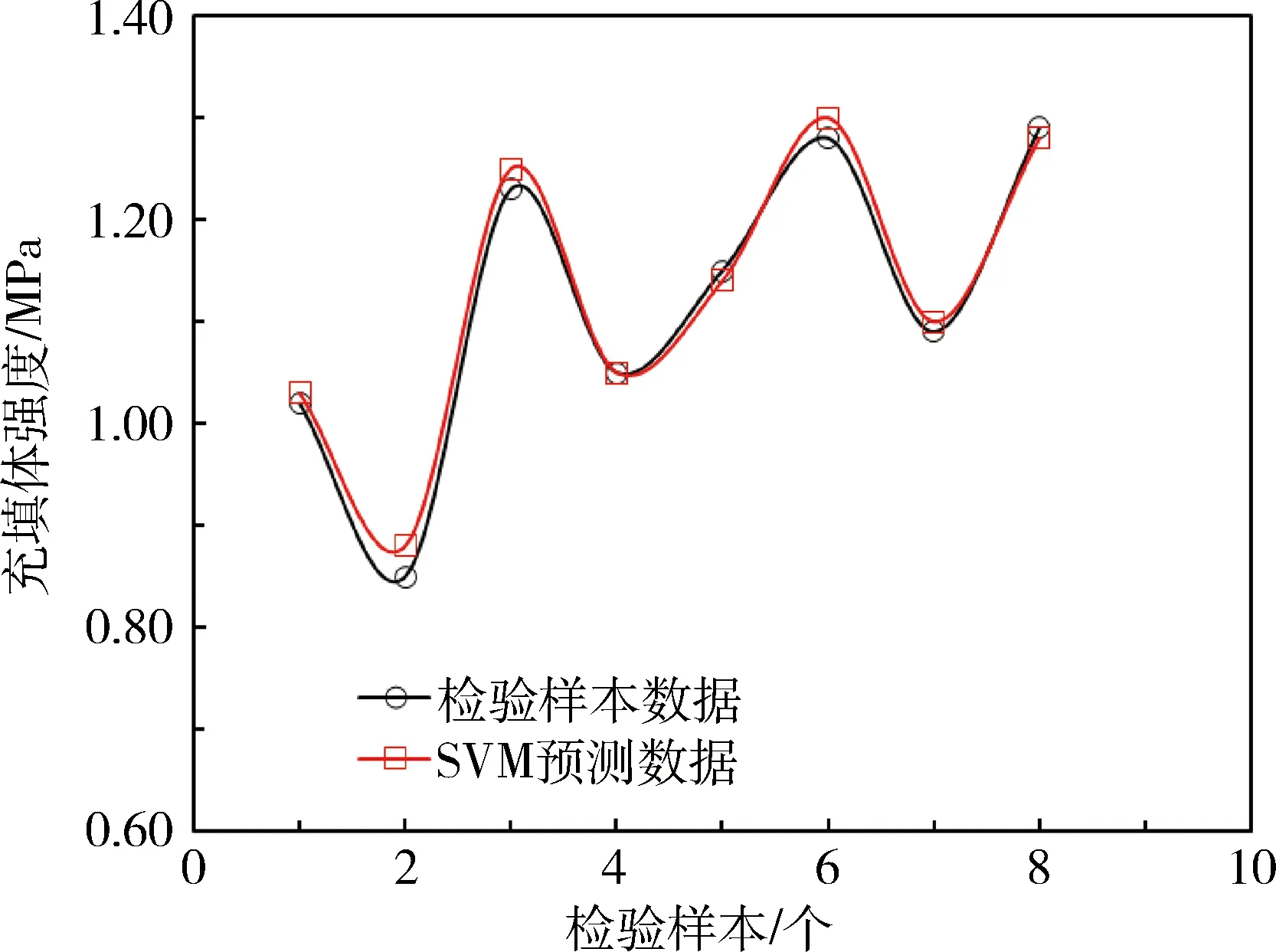
图4 检验样本的预测结果Fig.4 Test sample prediction results
3 三山岛金矿充填体强度匹配设计
三山岛金矿西山矿区采用空场嗣后充填采矿法进行回采,试验采场位于-780 m中段,采场矿体厚度为20 m,围岩稳固性中等,f=8,中段高度6 m,分段高度15 m,采场宽度7~12 m,采场长度100 m,一步骤回采矿房最大暴露面积为1 500 m2,二步骤回采矿柱最大暴露面积为600 m2。利用训练的SVM充填体强度匹配模型计算得一步骤矿房回采的充填体强度为1.02 MPa,二步骤矿柱回采的充填体强度为0.86 MPa。
根据矿山实际情况并结合充填体强度试验结果,在充填体质量浓度在70%~72%之间时,为确定合理灰砂比,对不同灰砂比条件下的充填体强度继续测试,测试结果见表3,从测试结果可以得出,推荐一步骤矿房回采的充填体灰砂比为1∶12,二步骤矿柱回采的充填体灰砂比为1∶16。根据推荐的灰砂比进行充填,充填体效果良好,采场稳定性良好,未发生充填体垮塌等事故。
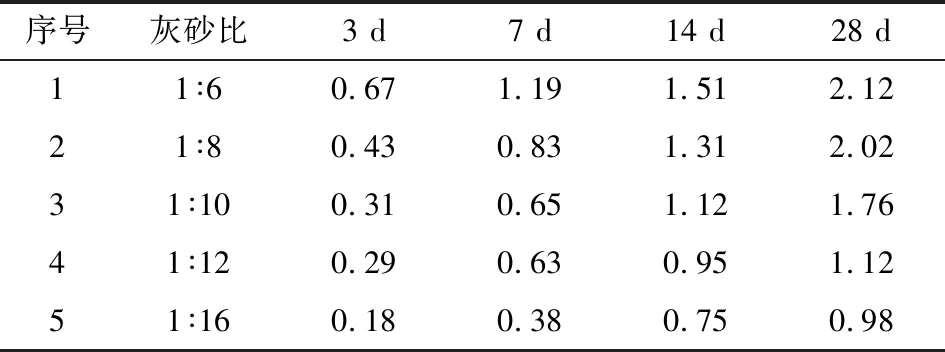
表3 充填体强度试验结果
4 结 论
1) 采用建立的SVM模型和BP模型对70组矿山实测充填体强度数据进行训练,对两种方法的预测数据与实测数据误差进行比较,结果显示SVM模型的预测精度更高。
2) 采用SVM模型对8组检验样本数据进行预测计算,预测值与检验样本原始值的平均误差仅为1.28%。
3) 采用该方法对三山岛金矿两步骤回采充填体的强度进行匹配,一步骤矿房匹配充填体强度1.02 MPa,二步骤矿柱匹配充填体强度0.86 MPa。
