孤立波边界对流线型箱梁静气动力系数的影响

张家玮，康啊真，祝兵，薛世豪，吴超

孤立波边界对流线型箱梁静气动力系数的影响

张家玮，康啊真，祝兵，薛世豪，吴超

(西南交通大学 桥梁工程系，四川 成都 610031)

近海台风波浪的气动干扰可能对桥面标高较低的近海桥梁主梁的气动特性产生显著影响。为研究孤立波边界对流线型箱梁的气动力系数的影响，针对流线型箱梁进行一系列参数化的风洞试验，并运用CFD方法模拟波浪边界影响下的二维风场，与试验结果进行验证。系统分析波峰位置、桥下净空、攻角和波高等条件对主梁气动力系数的影响。通过CFD流场分析对气动力系数变化的可能机理进行讨论。研究结果表明：相较于无波浪条件，随着波峰从上风向靠近主梁，主梁的气动力系数呈先降低后升高的趋势，在下风向梁体附近气动力系数达到极值，此后随着波峰远离，气动力系数逐渐减小。这是由于波浪与梁截面之间局部流场方向和压强发生变化。在桥下净空小于2倍的桥宽范围内，气动力系数变化幅度随桥下净空的减小而增大，随波高的增大而增大。

极端海浪；箱梁；气动力系数；风洞试验；桥下净空

台风天气不仅使桥址区风速增加，同时可能导致风暴潮和飓风波浪。桥址处的水位升高和海浪气动干扰，可能对近海桥梁主梁的气动特性产生显著影响，威胁主梁的安全。而目前在进行跨海桥梁的抖振分析和车桥耦合分析时，风荷载和浪荷载常进行简单叠加，未考虑波浪边界的存在对上部结构气动力的影响[1]。现有研究中有大量针对波浪形边界对海上风场的影响[2−5]，但结构的存在对风场也会产生影响。关于风浪联合作用对结构响应，GUO 等[6]通过1:100风洞水槽实验研究了单风、单浪和风−浪联合作用下桥塔模型的动态响应。刘海源等[7]进行了风浪流作用桥塔弹性模型试验研究，观测到当波浪周期与桥塔结构自振周期相同或接近时所发生的共振现象。桥梁断面气动力研究比较丰 富[8−11]，而通过风洞试验和数值模拟进行海浪气动干扰条件下桥梁结构气动性能的研究甚少，研究对象主要为机翼和导弹等结构。秦绪国等[12]基于数值模拟研究了波浪边界条件对机翼翼型气动性能的影响。李妍等[13]在导弹数值模拟中考虑了波浪要素的影响，定量研究了海浪边界对巡航导弹掠海飞行的影响。对于桥梁结构，徐进[14]基于数值模拟研究了桥下净空的影响对气动力的影响；汪荣绣[15]通过风洞试验研究了双峰波浪干扰流场条件下主梁静风荷载效应，但缺少机理分析和对波高等参数的系统研究。研究风浪联合作用下箱梁气动力特性需要建立两相流相互作用模型，作为基础研究，由于波浪传播速度相较于风速较小，本研究暂时忽略波浪传播速度对于风场的影响，静止的波浪边界可以近似模拟波浪的形状，为更深入的研究奠定基础。本文以某近海桥梁大跨度流线型箱梁为工程背景，基于风洞试验和CFD数值模拟研究极端波浪气动干扰下主梁节段静力气动力系数的影响。对桥梁及海洋平台等抗风设计提供借鉴。

1 主梁节段模型风洞试验

1.1 工程背景

以某近海大桥主梁为研究对象，主桥为双塔三跨布置的悬索桥，梁跨布置为264+918+365 m。主加劲梁采用扁平钢箱梁，梁宽34.0 m，梁高3.4 m，桥塔采用钢筋混凝土结构，加劲梁标准断面如图1所示。

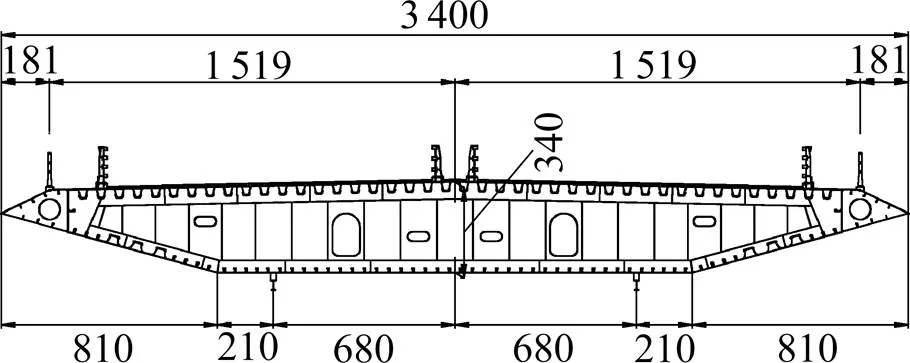
单位：cm

1.2 节段模型及试验参数

本文以裸梁为研究对象，主梁节段模型采用1:50的几何缩尺比，模型长=2.095 m，宽=0.68 m，高=0.068 m。模型用红松木和层板制作。为模拟桥下净空变化，试验采用刚架和木板拼接模型调整风洞实验室的水平面。采用孤立波模型模拟台风或海啸引起的极端海浪，水深=0.032 m，波高=0.61 m，有效波长=2 m。波浪模型选用细木工板骨架和三合板制成。孤立波公式如下：

式中：0为孤立波面相对于水平面的竖向坐标；0为孤立波面相对于波峰的水平坐标，m。

试验在西南交通大学工业风洞(XNJD-1)第2试验段中进行。图2为静力气动力实验。模型由气动力专用侧壁支撑固定于三分量应变式天平，来流为均匀流，风速=15 m/s。使用数据采集仪测量静风荷载下的阻力、升力和力矩，按式(2)~(4)计算风轴下的气动力系数；试验波浪的波峰不同水平位置/=0，±1.5，±1.0，±0.5，±0.25(为波峰中心线与梁轴线的水平距离，背浪侧为正)，如图3所示。模型桥下净空=0.48，0.64，0.80和0.96 m。

图2 边界影响下静气动力系数节段模型测力试验

图3 波浪水平位置

1.3 静气动力系数

主梁断面在风轴坐标系下的静气动力系数计算式如下。

阻力系数：

升力系数：

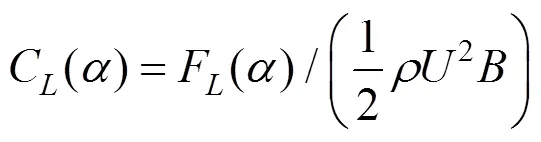
力矩系数：

式中：表示来流风速；为空气密度；取1.225 kg/m3。F，F和M分别表示单位长度横桥向阻力、竖向升力及俯仰力矩；为模型攻角；为参考宽度，取箱梁顶板宽度0.68 m；为参考高度，取箱梁中心高度0.068 m。

2 CFD数值模拟

由于主梁外形沿主跨方向不变，可简化模拟二维流场，流动为非定常不可压。采用Fluent软件，基于雷诺时均N-S方程，湍流模型为标准-模型，实现二维流场的模拟。压力速度耦合选用PISO算法，离散格式为二阶迎风插值，时间步长为10−5s。计算结果取气动力系数时程均值。

为更好实现对比，与节段模型实验相同，采用缩尺后的模型进行建模。上边界到断面中心的距离为0.98 m，下边界距离梁底标高随不同的净空而发生变化。入口采用速度边界，距断面中心12 m，出口距断面中心22 m，采用压力出口边界，主梁外壁为无滑移的壁面，近壁面以标准壁面函数处理。

首层网格单元厚度为0.01 mm，单元厚度自内而外按等比数列递增，相邻网格单元膨胀率控制不超过1.1。在流场变化剧烈的地方划分较密的网格，然后逐渐过渡，外部网格划分较疏，以使网格更能适应流场的变化，最大网格尺寸为0.02 m。网格数约30万。流场网格如图4所示。

表1列出了一些典型工况气动力系数的CFD 计算值与试验结果，对比表明，CFD可以较准确地反映C，C和C随攻角、波浪位置的变化趋势。其中，C的模拟精度最高，C次之，C的模拟精度稍差，但由于其值很小，接近于0，误差属于可接受范围。

(a) 流场整体；(b) 梁体局部

表1 典型工况气动力系数的CFD计算值与实验值的对比

3 极端海浪干扰对箱梁气动特性影响

3.1 风洞试验阻塞效应的影响

由于净空垫高导致风洞试验的阻塞比增加。相关风洞试验研究认为需要保证阻塞比小于2%，否则阻塞效应无法忽略。也有相关研究[16−17]认为，将阻塞比控制在5%以内就可以忽略阻塞效应。

本试验阻塞比小于4%，为使测得数据更符合实际，本文采用Mecrker半经验修正方法[18]，对试验C系数进行修正。由阻塞效应引起风速的增加可表示为：

修正后的阻力系数：

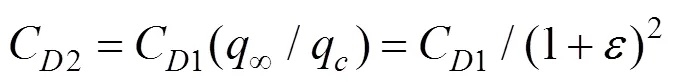
图5 阻塞比修正后的CD系数

3.2 波峰水平位置的影响

图6给出了波峰不同水平位置/=−0.15~0.15共9个位置，主梁阻力系数随波峰水平位置的变化规律。

(a) CD系数；(b) CL系数；(c) CM系数

当波浪在主梁迎风一侧/=−1.5时，气动力系数与无波浪条件相比变小；随着波浪向主梁靠近，阻力系数先下降，约在/=−1.0时，达到最小值；当波峰向主梁后方移动时，气动力系数逐渐增大，尤其当波峰移动到主梁后方/=0.5附近时达到峰值，此后随着波峰继续移动，气动力系数减小，向无波浪条件趋近。

图5给出了攻角为−2°，0°和2°时，气动力系数随波浪水平位置的变化曲线，由图5可见，各攻角下气动力系数的整体变化趋势相同；−2°和0°攻角下，最大阻力系数大于无波浪工况，2°攻角下阻力系数整体小于无波浪工况；−2°，0°和2°攻角下，波浪影响下的最大阻力系数与无波浪条件的阻力系数差异分别为60%，49%，−4%。

无波浪工况和波浪影响下工况的升力系数和扭矩系数峰值差异更大；无波浪条件下升力系数整体为负值，而在波浪影响下，在/=0~1.0区域，升力系数出现正值，波浪影响下最大和最小升力系数均与无波浪条件升力系数存在较大差异；−2°，0°和2°攻角下，波浪影响下的最大升力系数与无波浪条件的升力系数差异分别为85%，215%和1 337%。

图7为−2°攻角下不同波峰水平位置工况的流场压力分布，将气动力系数随波峰水平位置变化的原因归结如下：

(a) 无波浪，流场压力云图；(b) x/B=−1.0，流场压力云图；(c) x/B=+0.5，流场压力云图

无波浪时，截面的迎风面和背风面为正压区，上表面存在正压区和负压区，下表面为负压区。当波浪在主梁迎风一侧时，波浪的遮挡效应使得箱梁附近区域的风压及流场分布发生较大变化。当/=−1.0时，波峰的存在使得波峰梁底之间的区域由于局部流场加速作用出现负压区，迎风面正压区的范围减小，且正压最大的峰值点逐渐向截面上部移动。下表面负压区的范围明显增大，且负压的峰值增大。波浪边界使得截面附近的流速方向出现向下分量。以上原因共同导致阻力系数相较于无波浪条件减小，升力系数向负值变化。

随着波峰位置的右移，梁底风场加速区域也慢慢右移，当/=0.5时，波浪边界使得截面附近的流速方向出现向上分量，迎风面正压最大的峰值点向截面下部移动，背风面由正压区变为负压区，导致阻力系数和升力系数相较于无波浪条件有所增大。

3.3 桥下净空和波高的影响

图8分别给出不同桥下净空下−2°工况气动力系数随波峰水平位置变化的曲线，其中孤立波波高=0.16 m。由图8可知，在桥下净空小于2倍的桥宽范围内，不同净空下气动力系数受波浪位置影响趋势基本一致；随着桥下净空减小，使得波峰与梁体之间的局部压缩区域变小，气动力系数受波峰位置影响显著，对应极值的差异增大。

(a) CD系数；(b) CL系数

(a) CD系数；(b) CL系数

阻力系数在不同桥下净空下的变化曲线有一定差异，阻力系数最大值在/=0~1.0之间，随桥下净空的减小，峰值更加靠前。桥下净空=0.64 m及更大的工况阻力系数在/=0.5附近达到峰值，在桥下净空=0.48 m时，阻力系数在/=0.25附近达到峰值，此后随波浪移动存在显著的减小趋势，在/=1.0达到极小值。说明桥下净空对梁体周围的流速及压强分布影响很大。由于桥下净空减小，波浪边界对流场的影响越大，梁底流速也明显加大，流场方向变化更加显著。

为研究孤立波波高对于气动力系数变化的影响，取桥下净空=0.48 m，攻角−2°，通过数值模拟对比了=0.13，0.16，0.19 m(原型波高6.5~9.5 m)条件下气动力系数随波浪位置移动的影响规律。原型波高参考了跨海大桥桥址区百年一遇重现期波高，并结合研究需要参考其他跨海大桥的海洋波浪环境增加了部分波高工况。图9给出同一桥下净空，不同波高工况气动力系数随波峰水平位置变化的曲线。由结果可知，对于同一桥下净空，随着边界波高的增加，波峰与梁体之间的局部压缩区域变小，气动力系数受波峰位置影响显著，同时由于波高的增加导致梁体前方的局部流场方向变化，使得阻力系数和升力系数的最小值趋向于波峰更加靠近结构的位置出现；阻力系数和升力系数的峰值位置几乎不随波高的变化而改变。

4 结论

1) 相较于无波浪条件，随着波峰靠近主梁，主梁的气动力系数呈先降低后升高的趋势，在波峰位于背浪侧约0.5~1倍梁宽时达到峰值，此后随着波峰远离，主梁的气动力系数逐渐减小。

2) 当波浪处于主梁迎风向时，波峰对于波浪后方风场的影响，导致局部流向出现向下分量，且导致梁体和波浪间的局部流场加速，截面下方负压区增大，导致阻力和升力相较于无波浪条件有所减小；当波峰在主梁后方约0.5倍梁宽处，局部流向出现向上分量，背浪侧变为负压区，导致阻力系数相较于无波浪条件有所增大，升力系数向正值 变化。

3) 在桥下净空小于2倍的桥宽范围内，桥下净空的减小和波高的增加都导致气动力系数受波峰位置影响更加显著。

4) 本研究过程中，忽略了波浪传播速度对于风场的影响，而实际过程中波浪的运动对气动力的变化存在一定影响。在未来的研究中，会考虑到波浪的移动，分别采用波浪模型牵引系统和风浪联合水槽进行气动力的研究，比较刚体边界和水面边界的差异，分析气动力时程受到波浪运动的影响。

[1] 李永乐, 房忱, 向活跃. 风−浪联合作用下大跨度桥梁车−桥耦合振动分析[J]. 中国公路学报, 2018, 31(7): 119−125. LI Yongle, FANG Chen, XIANG Huoyue. Coupled vibration analysis of vehicle-bridge for long-span bridge under wind and wave[J]. China Journal of Highway and Transport, 2018, 31(7): 119−125.

[2] Buckles J, Hanratty T J, Adrian R J. Turbulent Flow over Large-amplitude wavy surfaces[J]. Journal of Fluid Mechanics, 1984, 140: 27−44.

[3] HU P, HAN Y, XU G, et al. Numerical simulation of wind fields at the bridge site in mountain-gorge terrain considering an updated curved boundary transition section[J]. Journal of Aerospace Engineering, 2018, 31(3): 04018008.

[4] 孙丽明, 曹曙阳, 李明, 等. 考虑波浪形底面影响的边界层风场大涡模拟[J]. 空气动力学学报, 2014, 32(4): 534−543.SUN Liming , CAO Shuyang, LI Ming, et al. Large-eddy simulation of fully developed turbulent flow over a wavy surface[J]. ACTA Aerodynamica Sinica, 2014, 32(4): 534−543.

[5] 许福友, 李文江, 张哲, 等. 海浪强干扰条件下风场特性风洞试验研究[C]// 第8届全国随机振动理论与应用学术会议暨第1届全国随机动力学学术会议, 成都, 2012: 203−238.XU Fuyou, LI Wenjiang, ZHANG Zhe, et al. Experimental research on wind flow field severely interfered by sea wave via wind tunnel[C]// The 8th National Random Vibration Theory and Applied Academic Conference & The 1st National Random Dynamics Academic Conference.Chengdu: China, 2012: 203−238.

[6] GUO A, LIU J, CHEN W, et al. Experimental study on the dynamic responses of a freestanding bridge tower subjected to coupled actions of wind and wave loads[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2016, 159: 36−47.

[7] 刘海源, 耿宝磊, 彭程. 风浪流作用桥塔弹性模型试验研究[J]. 水道港口, 2015, 36(6): 461−466.LIU Haiyuan, GENG Baolei, PENG Cheng. Experimental study on elastic model of bridge tower under wind, wave and current[J]. Journal of Waterway and Harbor, 2015, 36(6): 461−466.

[8] HAN Y, CHEN H, CAI C S, et al. Numerical analysis on the difference of drag force coefficients of bridge deck sections between the global force and pressure distribution methods[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2016, 159: 65−79.

[9] Seo J W, Kim H K, Park J, et al. Interference effect on vortex-induced vibration in a parallel twin cable-stayed bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 116: 7−20.

[10] 张亮亮, 吴波, 杨阳, 等. 附属构件及桥面粗糙度对近流线型宽体箱梁气动静力系数的影响[J]. 实验流体力学, 2016, 30(1): 74−80. ZHANG Liangliang, WU Bo, YANG Yang, et al. Effects of subsidiary members and deck surface roughness on the aerodynamic coefficients of static forces on a flat box girder[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(1): 74−80.

[11] 李少杰, 刘小兵, 杨群, 等. 分离双扁平箱梁气动力干扰效应研究[J]. 工程力学, 2017, 34(增1): 89−93.LI Shaojie, LIU Xiaobing, YANG Qun, et al. Study on interference effect of aerodynamic force of twin separate flat box girders[J]. Engineering Mechanics, 2017, 34(Suppl 1): 89−93.

[12] 秦绪国, 刘沛清, 屈秋林. 翼型波浪水面巡航地面效应数值模拟[J]. 北京航空航天大学学报, 2011, 37(3): 295−299. QIN Xuguo, LIU Peiqin, QU Qiulin. Numerical simulation on aerodynamics of airfoil flying over wavy water surface[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(3): 295−299.

[13] 李妍, 陈希, 费树岷. 海浪对巡航导弹掠海飞行气动性能的影响[J]. 弹箭与制导学报, 2014, 34(3): 129−132.LI Yan, CHEN Xi, FEI Shumin, et al. The research on influence of wave on pneumatic performance of sea-skimming cruise missile[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2014, 34(3): 129−132.

[14] 徐进. 桥下净空对大跨桥梁主梁气动特性的影响[D].长沙: 湖南大学, 2014. XU Jin. Effects of vertical clearance on aerodynamic characteristics of long-span bridge girders[D]. Changsha: Hunan University, 2014.

[15] 汪荣绣. 海浪气动干扰条件下桥梁气动性能试验研究[D]. 大连: 大连理工大学, 2014. WANG Rongxiu. Experimental research on aerodynamic performance of bridge interfered by rough waves[D]. Dalian: Dalian University of Technology, 2014.

[16] Kubo Y, Miyazaki M, Kato K. Effects of end plates and blockage of structural members on drag forces[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1989, 32(3): 329−342.

[17] Holmes J D. Wind loading of structures[M]. CRC Press, 2015.

[18] Mercker E. A blockage correction for automotive testing in a wind tunnel with closed test section[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1986, 22(2/3): 149−167.

[19] 张清林. 汽车模型风洞关键影响因素研究及数据后处理软件开发[D]. 长沙: 湖南大学, 2012. ZHANG Qinglin. Study on Influence Factor of automotive wind tunnel test and development of the data processing software[D]. Changsha: Hunan University, 2012.

Effect of solitary wave boundary on aerostatic coefficients of a streamlined box girder

ZHANG Jiawei, KANG Azhen, ZHU Bing, XUE Shihao, WU Chao

(Department of Bridge Engineering, Southwest Jiaotong University, Chengdu 610031, China)

The aerodynamic characteristics of the coastal bridges with low elevation are significantly affected by the aerodynamicinterference of coastalhurricane waves. To investigate the aerostatic coefficients of typical streamlined box girder under the influence of solitary waves, a series of parametric wind tunnel tests were conducted, and two-dimensional numerical wind tunnel was established by CFD which was validated by the experiment results. The effect of the horizontal position of the wave crest, vertical bridge clearance, wind attack angle and wave height on the aerostatic coefficient of the box girder were systematic analyzed. And the possible mechanics of aerostatic coefficient change were discussed through flow patterns analysis. The results show that, as the wave crest gradually approaches the girder, the aerostatic coefficient decreases firstly and then increases. The aerostatic coefficient reaches a maximum value when the wave crest locates at 0.5-1 times beam width behind the structure. As the wave crest moves away from the beam, the aerostatic coefficient gradually decreases. It is caused by the change in the direction and pressure of local flow field between wave surface and beam section. The variation amplitude of aerostatic coefficients increases with the decrease of bridge clearance, when vertical bridge clearance is less than twice of the girder width.

extreme wave; box-girder; aerostatic coefficients; wind tunnel tests; vertical bridge clearance

U441+；U446

A

1672 − 7029(2019)10−2497 − 08

10.19713/j.cnki.43−1423/u.2019.10.016

2018−12−11

国家自然科学基金资助项目(51178397)；国家自然科学基金(青年)基金资助项目(51708456)；四川省应用基础重大前沿项目(2017JY0003)

祝兵(1965−)，男，江苏无锡人，教授，博士，从事桥梁风浪耦合动力学研究；E−mail：zhubing126@126.com

(编辑 阳丽霞)