离散元表征的级配碎石加州承载比细观力学行为研究

彭安平，李亮，张智

离散元表征的级配碎石加州承载比细观力学行为研究

彭安平1, 2，李亮1，张智1

(1.中南大学 土木工程学院，湖南 长沙 410075；2. 湖南路桥建设集团有限责任公司，湖南 长沙 410075)

基于离散元法构建符合真实级配的石灰石碎石二维细观模型，确定模型的细观参数与加载速率，研究级配碎石的加州承载比(CBR)试验。通过对试验和模拟中贯入力−贯入量曲线以及CBR值进行对比验证，验证模型的合理性与正确性。分析加载后的主应力方向、接触力链和位移矢量等细观机制变化规律。分析加载速率、摩擦因数与刚度比等参数对石灰石碎石CBR值的影响。研究结果表明：随着加载速率的降低，CBR数值基本呈缓慢降低的趋势；集料的纵向变化明显于横向变化，离散元模型能够较好地反映级配碎石的细观作用机制；颗粒间摩擦因数的增加能够明显提高级配碎石的抗压能力，碎石体系的抗变形能力随着法向刚度大小增大而增大。

级配碎石；加州承载比；PFC2D；离散元模型；细观结构

级配碎石广泛用于道路工程建设当中，很多国家都采用加州承载比(CBR)作为衡量路基路面材料抵抗集中荷载的强度设计指标。然而，由于级配碎石存在显著的非线性力学性能和非连续介质结构，受到当前力学理论的限制，无法从理论上详细分析级配碎石的力学参数、实验条件与抗压力变形性能之间的关系。另外，传统的室内试验方法要求通过重复大量的测试数据，才能够分析出集料性能与加州承载比之间的规律来优化级配碎石的集料选择与设计，从而使得级配碎石的设计周期长、资源浪费大[1]。在级配构成与CBR方面，长安大学马骉 等[2]进行了相当详细的室内试验，包括对提高级配碎石的抗变形能力、动态回弹模量、抗剪切性能等方面进行了研究；Nunes等[3]利用加州承载比试验研究了用于路面施工的二次碎石材料，得到矿石和石片碎料的加州承载比分别为5%和35%；Mousa等[4]对混合不同含量碎石的再生沥青路面的回弹模量和加州承载比进行了研究；龚璐[5]通过对回弹模量、加州承载比、塑性变形等参数的影响因素进行分析并确定了级配碎石的优先级配设计等。在级配碎石力学特性的数值模拟方面，王丰胜[6]基于KENLAYER的计算模型对碎石级配的宏观力学性能进行了一系列研究探索；任皎龙[7]使用有限元数值模拟技术，对级配碎石的加州承载比的影响因素进行了较为全面的分析。Bigi等[8]研究了不同级配组成的级配碎石在不同含水量状态下的动三轴试验，同时对级配碎石在冻融过程中的力学特性进行了分析；Janoo等[9]研究了级配碎石中粗集料的三维形状、棱角性和表面纹理等因素对其性能的影响，规定了对集料等级进行评价的相关指标，并分析了不同尺寸式样的级配组成、集料规格、含水率和空隙率等参数对级配碎石性能的影响。鉴于级配碎石复杂而又相互影响的力学参数和加州承载比室内实验无法避免的缺点。以PFC2D为代表的离散元数值软件广泛应用于道路材料的力学特性研究[10−15]。因此，本文研究基于离散元法，对级配碎石CBR试验进行模拟和影响因素进行研究分析，探讨研究级配碎石微细观结构的手段。

1 室内试验

本文采用CBR值评价粒基层材料承载力，其表征了材料的竖向刚度和抗剪切能力。选用石灰岩质集料用作级配碎石其级配如图1所示，其原因如下：1) 石灰岩在轧制过程中易轧制成所需的形状，且较易满足级配要求。2)石灰岩中所含的碳酸盐在级配碎石基层施工过程中能够与水发生水化反应，可以在集料中发挥胶结作用，从而能够改善级配碎石力学特性。通过重型击实试验以获得其最大干密度为2.346 g/cm3及最佳含水率为4.85。最后，在此基础上进级配碎石的CBR试验，试件成型和室内试验详细描述可以参考文献[16]。

图1 石灰岩碎石级配图

根据CBR定义可知，其贯入规定量(2.5 mm和5 mm)时所需荷载与标准碎石贯入相同量时所需要荷载的比值，以百分率表示其所得到的CBR值。CBR计算公式如下：

式中：CBR-加州承载比；-贯入量为2.5 mm或5 mm时的荷载；P-贯入标准碎石2.5 mm时的标准荷载(7 000 kPa)或贯入标准碎石5 mm时的标准荷载(10 500 kPa)。

2 级配碎石CBR数值模拟方法

2.1 几何模型的建立

利用颗粒流软件PFC2D所构建的级配碎石加州承载比试验模型如图2所示，首先按照实际试验的预定尺寸创建矩形边界区域。在其边界范围内按照级配碎石的设计级配创建各档的集料颗粒。另外，考虑到集料的不规则形状和模型计算速率的影响，将粒径大于2.36 mm的粗集料利用clump模拟其不规则的形状特征，其中clump形状采用多种不同形状的集料二维图形，利用PFC2D内置命令将集料图形导入模型中并生成单一不规则集料以体现集料的不规则形态特性，同时将代表级配碎石圆盘颗粒随机替换成不规则的clump，以体现集料的随机分布以及不规则形状特性。而粒径小于2.36 mm的细集料统一采用粒径为2 mm的颗粒模拟其力学特性。

模型尺寸为150 mm×120 mm，由3 637个圆盘颗粒和898个clump组成。由于clump中的pebble颗粒相互之间无接触作用，故模型中实际存在4 535个计算单元。为模拟CBR试验的加载边界条件，在顶部生成尺寸大小为50 mm×50 mm的模型如图2所示，然后在压头两侧生成50 mm宽的clump模拟顶部荷载板作用。在生成期间，不可避免存在大量的颗粒重叠现象，造成颗粒之间的接触不平衡力过大影响模型计算的收敛。为减小颗粒间的不平衡力的影响，模型通过不断循环作用使颗粒之间的重叠量达到最小值。

图2 CBR试验数值模型

图3 测量圆分布图

模型加载后颗粒间会出现应力重分布的现象，应力重分布必然会导致颗粒间应力主方向发生偏转。因此为研究颗粒间应力主方向规律，通过measure命令在模型中设置一定数量的半径为5 mm的测量圆(如图3)以监测各处应力大小，以此测量模型中各部分的应力大小状况。

2.2 细观力学参数的选取

PFC模拟需要通过细观尺度颗粒之间的相互作用来反映宏观尺度级配碎石整体的力学特性，而模型中利用颗粒间接触模型反映颗粒间的力学特性如图4所示。CBR数值模型中石灰石碎石可根据粒径大小分为粗集料(＞2.36 mm)和细集料(≤2.36 mm)2种类型。因此，模型中主要存在3种接触：细集料内部接触、粗细集料之间的接触以及粗集料之间的接触。

图4 颗粒间接触界面

石灰岩碎石中含有碳酸盐，其在级配碎石施工过程中能够与水发生水化反应，致使细集料在模型中能够起到胶结作用。因此，利用linear(图5)模拟粗集料之间的力学特性，而利用linearcbond(图6)接触模型模拟细集料之间的包括胶结等力学作用。

图5 线性模型

(a) 未黏结；(b) 黏结

黏结时线性接触黏结模型线性部分的力−位移法则：如果接触受到的法向力超过其抗拉强度时，法向黏结破坏且接触的法向和切向力都会被重新置零。如果切向力超过其具有的抗剪强度时，切向黏结破坏并且摩擦因数和法向力决定的摩阻力会限制颗粒的滑动。相反，如果接触所受到的法向和切向力未超过其强度限制，即接触处于黏结状态时其力学特性表现为线性接触模型。

本文根据文献[16]中的级配碎石的宏细观参数。经过多次的试算和调整，选取的模型中接触细观参数如表1所示。级配碎石的CBR试验属于准静态问题，一般采用较大的阻尼(β，β)，比如本文采用法向与切向阻尼比均为0.7，以提高计算的收敛速度，使系统迅速达到稳定状态。

2.3 加载条件的模拟

级配碎石CBR试验的加载速率为1~1.25 mm/min，如果模型无法按照真实的速率计算。因此，为提高计算效率，选择最佳加载速率以保证数值模拟的准确性，通过后续加载速率的分析，选择0.015 m/s作为模型的加载速率。在加载期间，压头以0.015 m/s的恒定速率向集料施加力的作用，直到贯入深度为3.5 mm时停止加载。另外，为模拟加载试件顶面的6 kg荷载板，给荷载板添加力，使其与重力之等效于6 kg荷载板的作用。

表1 模型中材料细观力学参数

2.4 可靠性验证

为研究碎石的竖向刚度以及剪切能力，进行了级配碎石的CBR室内试验和数值模拟试验。同时，分别记录了2类试验各自的贯入力随贯入量的变化曲线以及贯入量为2.5 mm时的CBR值。图7表示贯入深度为3.5 mm时的模型状态。由图7可知，模拟压头下方有限区域(如图位移值大的集料)内发生移动，并且压头的扰动作用明显。

图7 模型破坏状态

图8表示试验与模拟得到的曲线趋势对比图。由图可知，模拟与试验曲线的发展规律基本吻合，其中模拟出现几次波动，主要由于初期作用在颗粒上的力与荷载板所受的力反复平衡所致。另外，由表2中CBR值相差不大且保持在4.75%。由于是二维模拟，故差值没有三维模拟小一些，但是二维模拟其变化规律很有意义。表明通过建立正确的离散元模型和输入合理的参数，使用离散法可以准确的模拟级配碎石的CBR试验。

图8 CBR试验与数值模拟曲线对比

表2 CBR室内实验结果与数值模拟结果的对比

3 结果与分析

3.1 加载速率

由于受到计算效率的影响，模拟加载速率难以与实际试验相一致。利用不同的加载速率将影响模拟结果对试验对比精度从而影响模拟的准确性。为了选择最佳加载速率，故研究不同速率对CBR值的影响，其中选取的加载速度为：0.5，0.1，0.05，0.015和0.01 m/s。图9表示不同加载速率的贯入力与贯入量曲线，图中随着加载速率的减小曲线的变化趋势逐渐相近，尤其是速率0.015 m/s与0.01 m/s变化趋势较为相近。说明随着加载速率的减小，贯入力受速度影响所导致的变化逐渐趋于稳定。

图9 不同加载速率的贯入力与贯入量曲线

由图10可知，级配碎石的CBR值随着速率的减小逐渐表现出缓慢降低的趋势。当速率大于0.015 m/s时，贯入量为2.5 mm时的CBR值随着速率的减小逐渐降低，说明当速率大于0.015 m/s时，速率明显会对CBR值产生影响。其次，当速率小于等于0.015 m/s时，随着速率的减小拉应力峰值大小变化基本趋于平缓，说明当速率小于等于0.015 m/s时，速率的变化量对应力峰值影响甚微，甚至可以忽略不计。因此，基于模型计算效率和准确性等方面考虑，在后续研究沥青混合料的细观参数对力学特性的影响中，模型采用0.015 m/s作为最佳加载速率。

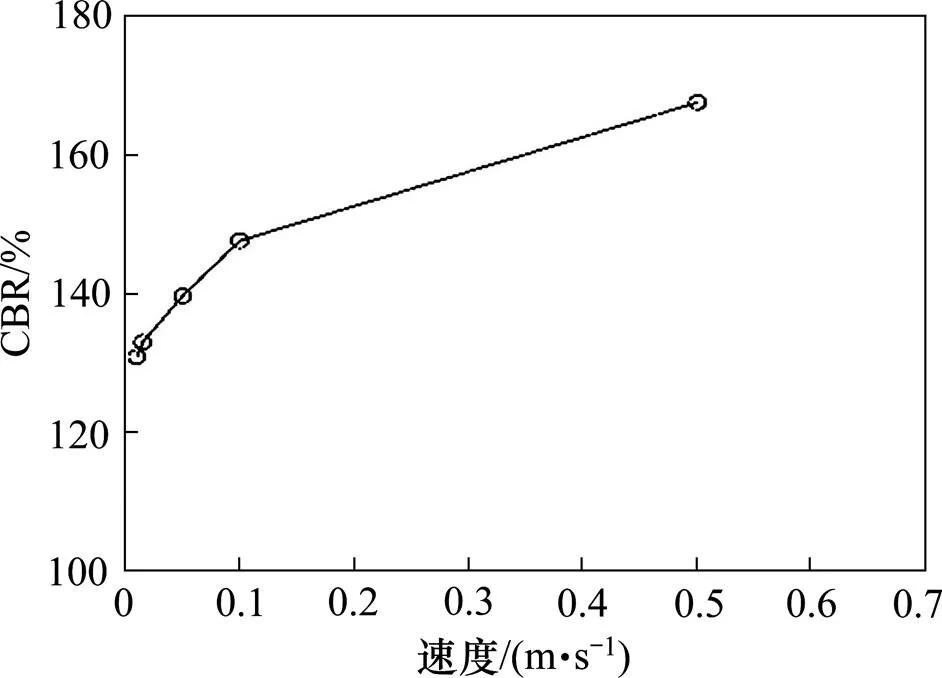
图10 速度对CBR的影响

3.2 模型细观机制分析

当压头贯入模型时，颗粒间会发生嵌挤、摩擦作用，集料内部会发生应力重分布的现象，应力重分布必然会导致应力主方向发生偏转。因此，基于应力主方向的偏转情况、量化力链分布以及粗骨料量化速度矢量分布情况，对贯入后模型中的受力形态以及演变规律进行分析。应力主方向0的计算表达式为[17]：

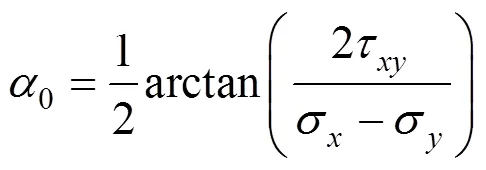
式中：，和分别表示水平、切向和竖向应力。测量圆能够监测出各个测量圆范围内水平应力、切向应力和竖向应力大小，然后根据式(2)计算出应力主方向。为了能方便形象的表示每个测量圆内应力主方向分布情况，模型中采用离散元裂隙网络表示应力主方向的分布状况。

图11表示接触力以及应力主方向分布规律，图中接触线条粗细表示作用力的大小即线条越粗作用力越大。其中图11(a)表示初始状态的接触力及主应力方向分布规律，此时压头尚未作用于试样表面，压头下部区域主应力方向无规律分布。当压头贯入量为2.5 mm时，压头底部区域会出现明显的应力集中现象且逐渐向下延伸，而模型两侧作用力相对较小，接触力的纵向变化比横向变化相对明显。压头底部(图中矩形虚线内)的主应力方向在贯入量为0时，主应力方向分布表现不规则，而贯入量为2.5 mm时，由于压头贯入的作用集料已经形成主要受力骨架，主应力方向表现为是竖直规则排列，压头两侧反而表现为不规则分布状态。是由于压头下部区域主要承压，而两侧荷载板的存在颗粒能够向两侧向上稍稍移动。因此，主应力方向能够在加载中较好的反映模型内部的受力方向分布 规律。

(a) 0.0 mm；(b) 3.5 mm

图12表示级配碎石在不同贯入量时主应力方向以及粗集料速度矢量分布规律，图中箭头表示颗粒速度矢量大小，箭头方向为颗粒运动方向，箭头大小代表颗粒速度大小，箭头长度越大也就位移越大。当压头贯入量为0.5 mm时，速度矢量仅存在压头下方及两侧有限区域内，其它区域均为点状分布，压头下部的主应力方向仅在顶部一小部分区域规则竖直排放，表明此时的集料仅在表明发生轻微扰动；当贯入量为1.5 mm时，压头底部区域的集料速度矢量自压头下呈扩散型向下方扩展并且主应力方向竖直向上分布，表面颗粒快速迁移的同时也存在主要承载，另外，压头两侧区域的速度矢量减小，由于荷载板压力与颗粒受力达到平衡致使速度放缓。当贯入量为2.5 mm时，速度矢量与主应力方向与贯入量为1.5时类似，致使速度大小在减缓，这是由于集料在贯入力作用下逐渐密实，同时模型两侧速度矢量式中处于点状分布，集料扰动不明显，表明速度矢量的纵向变化比横向变化明显。

(a) 0.005 mm；(b) 0.015 mm；(c) 0.002 5 mm

3.3 摩擦因数的影响

为研究级配碎石之间摩擦因数对CBR值的力学影响，进行了一系列不同摩擦因数(0.12，0.22，0.32，0.42，0.62)的数值模拟试验。不同摩擦因数下级配碎石贯入应力与贯入量曲线如图13所示。图中贯入力曲线随着摩擦因数的增大其上升趋势由平缓逐渐变为陡峭。由图14可知，摩擦因数在0.12~0.62范围内，CBR值随着摩擦因数的增大而逐渐增大。这是由于摩擦因数越大，集料表面越粗糙，集料间越难以发生相对移动，故集料体系更加稳定，且在模型集料体系越稳固，级配碎石抵抗荷载的能力就越强，因此级配碎石的CBR值相对也就越大。同时也间接证明了集料的表面纹理粗糙度对提高级配碎石CBR具有积极意义。

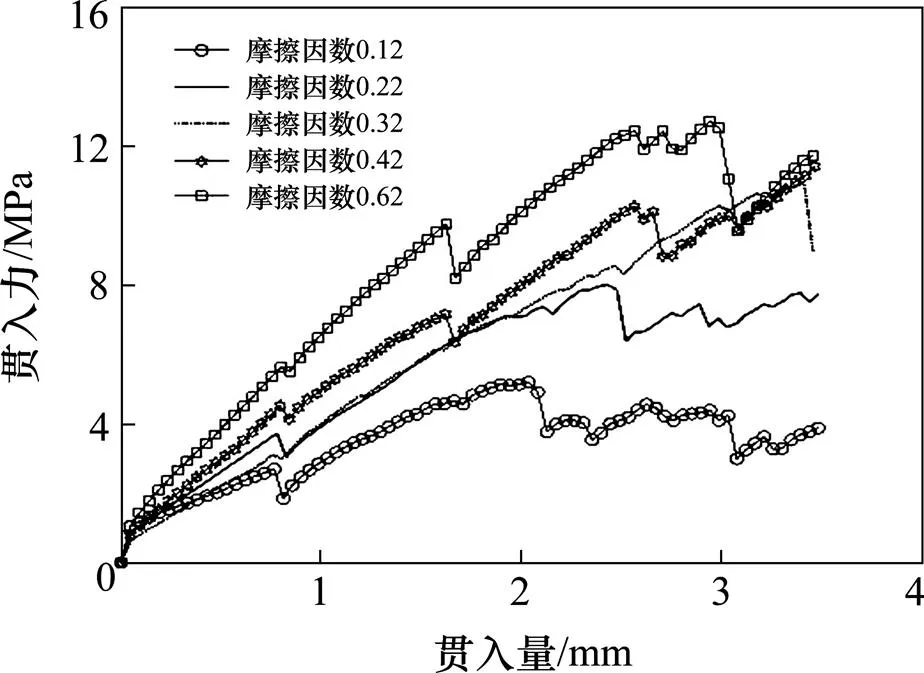
图13 不同摩擦因数的贯入力与贯入量曲线

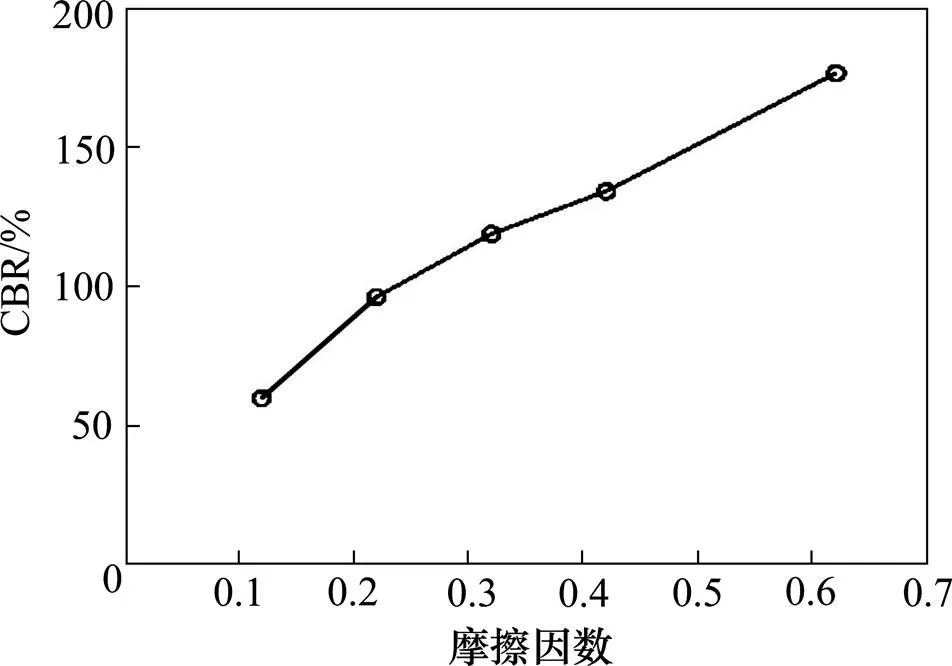
图14 CBR随摩擦因数的变化趋势

3.4 刚度比的影响

为研究颗粒间法向与切向刚度比对级配碎石细观力学特性的影响，进行一系列不同刚度比(0.41，2.41，3.41，4.41，5.41和6.41)的CBR模拟。图15表示不同刚度比条件下贯入力随贯入量变化曲线。与摩擦因数相比，刚度比的变化对贯入力曲线形态的变化影响相对较小。图16中CBR值随着刚度比的增加而逐渐下降，且两者之间存在一定的线性关系。是由于在集料弹性模量不变的情况下，CBR随着刚度比的减小而减小，表明碎石的法向刚度在减小，集料在荷载作用下的抗变形能力降低，导致CBR值降低。但是刚度比代表着碎石本身的力学特性，并不影响颗粒的表面接触状态，进而不会对颗粒间的相对移动有所影响，故贯入力曲线形态及CBR值大小相差不大。

图15 不同刚度比的贯入量与贯入力曲线

图16 CBR随刚度比的变化趋势

4 结论

1) 级配碎石CBR值随着速率的减小逐渐呈缓慢降低的趋势，当速率小于0.015 m/s时，速率对间接拉伸强度影响很小。故0.015 m/s作为最佳速率能够节省计算时间。

2) 随着贯入量的增大，主应力方向以竖直向上的方式规则排列在压头作用区域，细观接触力在压头处应力集中并向底部扩展，速度矢量自压头下呈扩散型向下方扩展。表明纵向变化明显于横向，模型能够较好地反映级配碎石的细观作用机制。

3) 贯入力随着摩擦因数的增大而增大，其趋势由平缓变陡峭；CBR值随着摩擦因数的增大逐渐增大且两者存在一定的线性关系。间接证明集料的表面纹理粗糙度对提高级配碎石CBR具有积极意义。

4) 随着刚度比的增大，级配碎石CBR值逐渐下降且幅度不大，但贯入力曲线形态的变化不大。表明碎石体系的抗变形能力主要与法向刚度大小有关。

由于计算效率的限制，难以细致的模拟2 mm以下的集料和矿粉等微小颗粒，从而无法研究两者的最佳用量，将在以后通过高性能计算机加以解决，这对推动级配碎石科学技术的发展具有重要意义。

[1] 谢远勇, 李改. 级配碎石动态CBR试验研究[J]. 公路工程, 2014, 39(2): 5−8. XIE Yuanyong, LI Gai. Experimental research on dynamic CBR of aggregate crushed stone[J]. Highway Engineering, 2014, 39(2): 5−8.

[2] 马骉, 王秉纲. 基于抗变形能力的级配碎石组成设计方法[J]. 长安大学学报(自然科学版), 2007, 27(5): 1−5. MA Biao, WANG Binggang. Graded and broken stone composing design method based on deformation resistance[J]. Journal of Chang’an University (Natural Science Edition), 2007, 27(5): 1−5.

[3] Nunes M C M, Bridges M G, Dawson A R. Assessment of secondary materials for pavement construction: Technical and environmental aspects[J]. Waste Management, 1996, 16(1/3): 87−96.

[4] Mousa E, Azam A, Elshabrawy M, et al. Laboratory characterization of reclaimed asphalt pavement for road construction in Egypt[J]. Canadian Journal of Civil Engineering, 2017, 44(2): 134−137.

[5] 龚璐. 级配碎石基层级配设计及应用研究[D]. 长沙: 长沙理工大学, 2008. GONG Lu. The research on grading design and application of unbound stone aggregates base[D]. Changsha: Changsha University of Science & Technology, 2008.

[6] 王丰胜. 影响级配碎石模量的结构因素敏感性分析[J]. 合肥工业大学学报(自然科学版), 2009, 32(9): 1414− 1417. WANG Fengsheng. Sensitivity analysis of the factors influencing the modulus of graded broken stone[J]. Journal of Hefei University of Technology (Natural Science Edition), 2009, 32(9): 1414−1417.

[7] 任皎龙. 级配碎石CBR数值试验方法及其应用[D]. 西安: 长安大学, 2011. REN Jiaolong. CBR simulation test method of graded broken stone and its appliance[D]. Xi’an: Chang’an University, 2011.

[8] Bigi S R, Berg R L. Material testing and initial pavement design modeling[J]. Material Testing & Initial Pavement Design Modeling, 1996, 23(3): 123−128.

[9] Janoo V C, Bayer J J. The effect of aggregate angularity on base course performance[J]. Effect of Aggregate Angularity on Base Course Performance, 2001, 33(1): 23−29.

[10] 王端宜, 赵熙. 沥青混合料单轴压缩试验的离散元仿真[J]. 华南理工大学学报(自然科学版), 2009, 37(7): 37−41. WANG Duanyi, ZHAO Xi. Simulation of uniaxial compression test for asphalt mixture with discrete element method[J]. Journal of South China University of Technology (Natural Science Edition), 2009, 37(7): 37− 41.

[11] Khattak M J, Khattab A, Rizvi H R, et al. Imaged-based discrete element modeling of hot mix asphalt mixtures[J]. Materials & Structures, 2015, 48(8): 2417−2430.

[12] 蒋应军, 李思超, 王天林. 级配碎石动三轴试验的数值模拟方法[J]. 东南大学学报(自然科学版), 2013, 43(3): 604−609. JIANG Yingjun, LI Sichao, WANG Tianlin. Numerical method of dynamic triaxial test on graded crushed rock[J]. Journal of Southeast University (Natural Science Edition), 2013, 43(3): 604−609.

[13] Zeghal M. Discrete element method investigation of the resilient behavior of granular materials[J]. Journal of Transportation Engineering, 2004, 130(4): 503−509.

[14] XIAO Y, Tutumluer E. Gradation and packing characteristics affecting stability of granular materials: Aggregate imaging-based discrete element modeling approach[J]. International Journal of Geomechanics, 2016, 17(3): 0401−0464.

[15] 蒋应军, 任皎龙, 李頔, 等. 矿料强嵌挤骨架密实级配的PFC2D数值试验研究[J]. 华南理工大学学报(自然科学版), 2012, 40(2): 92−98. JIANG Yingjun, REN Jiaolong, LI Di, et al. Investigation into close-grained gradation of aggregates skeleton under strong interlocked force via PFC2D numerical test[J]. Journal of South China University of Technology (Natural Science Edition), 2012, 40(2): 92−98.

[16] ZHANG J U, LI J, YAO Y S. Geometric anisotropy modeling and shear behavior evaluation of graded crushed rocks[J]. Construction and Building Materials, 2018, 183(3): 346−355.

[17] 赖汉江. 桩承式加筋路堤土拱形成—演化机理及承载特性宏细观分析[D]. 武汉: 华中科技大学, 2016. LAI Hanjian. Analysis of formation-evolution mechanism and bearing characteristics of soil arching within a piled embankment[D]. Wuhan: Huazhong University of Science & Technology, 2016.

Study on the meso-mechanical behavior of California bearing ratio of graded gravel with discrete element method

PENG Anping1, 2, LI Liang1, ZHANG Zhi1

(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. Hunan Road & Bridge Construction Group Co., Ltd, Changsha 410075, China)

A two-dimensional discrete element model of a graded gravel material with real graduation is developed based on discrete element software PFC2D to simulate and analyze the California bearing ratio (CBR) of a graded gravel material. The results of the force-penetration value curve and CBR value from the discrete element simulation were compared with actual test results and analyze the error and its source of the numerical model, which validated reasonability of the model. Then, the model was applied to study the micro-mechanism variation rule of the main stress direction, contact force chain and displacement vector of the CBR test of a graded gravel material, e.g., it also study the effects of various loading speeds, different friction coefficients and stiffness ratio of particles on the CBR of the material. The results indicate that the CBR value decreases slowly with the decrease of loading rate. The longitudinal variation of aggregate is more obvious than the transverse variation, and the discrete element model can better reflect the micro-mechanism of graded aggregates In addition, the increase of friction coefficient between particles cannot obviously improve the compressive ability of the graded gravel and the deformation resistance of gravel system increases with the increase of normal stiffness.

graded gravel; California bearing ratio; PFC2D; discrete element model; micro-structure

U414.103

A

1672 − 7029(2019)10− 2467 − 08

10.19713/j.cnki.43−1423/u.2019.10.012

2019−01−16

湖南省交通厅交通项目(2016-22)；国家自然科学基金资助项目(51308554)

彭安平(1974−)，男，湖南邵阳人，高级工程师，从事路基路面工程方面的科学研究；E−mail：663357762@qq.com

(编辑 涂鹏)