“简易方程”复习指南

◎刘 玲

一、知识梳理

1.用字母表示数

在含有字母的式子里，加号、减号、除号都不能省略。含有字母的乘法算式中，乘号可以用“·”代替，或省略不写。

2.方程

含有未知数的等式叫作方程。方程必须具备两个条件：一是等式，二是含有未知数，二者缺一不可。

3.方程的解

使方程左右两边相等的未知数的值，叫作方程的解。

4.解方程

求方程解的过程，叫作解方程。方程左右两边同时加上或减去同一个数，方程左右两边仍然相等；方程左右两边同时乘以或除以同一个不为0的数，方程左右两边仍然相等。

方程的解是一个未知数的值（数），它是使方程左右两边相等的未知数的值。而解方程是求这个数的计算过程。

5.列方程解应用题

列方程解应用题一般可分为如下四个步骤：

（1）弄清题意，找出未知数并用x表示；

（2）找出题中数量间的等量关系；

（3）列方程，求未知数x；

（4）检验并写出答案。

二、典例精析

例1：工地上有x吨水泥，每天用去3.5吨，用了b天。（1）用字母表示剩下的吨数；（2）当x=60，b=9时，还剩下多少吨水泥？

【分析与解】根据“每天用去的水泥×用去的天数=用去水泥的总吨数”的数量关系，可以写出用去水泥的吨数为3.5b；剩下的吨数可以用“水泥的总吨数-用去的吨数”得出。

解：（1）剩下的吨数是x-3.5b。

（2） 当x=60，b=9时，60-3.5×9=60-31.5=28.5（吨）

答：（1）剩下的吨数是x-3.5b吨；（2）还剩下28.5吨水泥。

根据字母的值，求含有字母的式子的值（可以不写出单位名称）。

例2：下面的式子中哪些是方程？

（1）a+b=b+a （2）10=6+4 （3）b+46

（4）3x-2=31 （5）2（5+y）=20 （6）15+2x＞20

【分析与解】判断一个式子是否是方程，主要看两个条件：一是等式，二是含有未知数。本题中的6个式子（1）（2）（4）（5）是等式，其中含有未知数的只有（4）和（5）。

解：（4）和（5）是方程。

例3：解方程：2x-0.8×5=16。

【分析与解】先把能算的“0.8×5”算出来，将方程“2x-0.8×5=16”转化成“2x-4=16”，再根据等式的基本性质求解，即等式两边同时加上4，除以2。

解：2x-0.8×5=16

2x-4=16

2x-4+4=16+4

2x=20

x=10

例4：红光小学买来4箱白粉笔和6箱红粉笔，一共用去311.2元。每箱白粉笔25元，每箱红粉笔多少元？

【分析与解】由“4箱白粉笔和6箱红粉笔，一共用去311.2元”可以列出数量关系：4箱白粉笔的钱数+6箱红粉笔的钱数=311.2。4箱白粉笔的钱数是25×4=100元。要求6箱红粉笔的钱数是多少元，可以设每箱红粉笔x元。那么6箱就是6x元，从而可列出方程。

解：设每箱红粉笔x元。

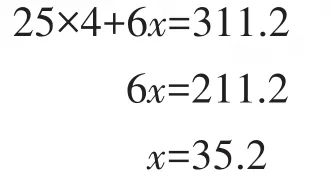
答：每箱红粉笔35.2元。