热挡板设计参数对涡声耦合压力振荡影响研究*

2019-11-13赵小锋孙兵兵李军强

弹箭与制导学报 2019年3期

赵小锋，孙兵兵，李军强

(1 海军装备部，北京 100000； 2 西安近代化学研究所，西安 710065)

0 引言

随着军事需求对推力要求的不断提高，分段式装药设计逐渐被大型固体火箭发动机采用,较好的完成了助推任务。但其弹道曲线或多或少存在压力振荡问题，严重时甚至影响发动机的正常工作，造成任务失败，如Ariane 5、RSRM及Titan IV等[1]。为了研究该问题，国内外许多学者做了大量的研究工作。通过Flandro[2]、Brown[3]、Anthoine[4-5]等人多年的研究，把该现象称为“涡声耦合”，解释了出现压力振荡的机理，并得到了一些可靠有用的抑制措施。国内的李强[6]、秦飞[7]、张翔宇[8]、王健儒[9]、许团委[10]、苏万兴[11]以及张峤[12]等人也展开了研究，从理论计算与实验等方面研究了该问题，为工程设计人员提供了一定的理论指导。但无论是实验还是理论计算均缺乏必要的数据来指导热挡板参数设计，不利于大型分段式发动机的设计。因此，文中基于阿丽亚娜5型运载火箭发动机的缩比模型,利用大涡模拟方法开展了数值研究，研究了热挡板高度和弯曲角度等设计参数对涡声耦合压力振荡的影响。

1 计算模型及边界条件

文献[5-12]计算结果表明，大涡模拟能够精确计算发动机燃烧室内由流动引起的压力振荡问题，因此采用大涡模拟来进行数值计算研究，详细的控制方程、亚格子模型及数值方法见文献[11]。

以阿丽亚娜5型运载火箭发动机缩比模型的1/30作为研究对象，为了计算方便，计算模型采用二维轴对称模型。

参照文献[11]设置边界条件，具体如图1所示。为了准确记录燃烧室内压力的振频与振幅特性，分别对发动机头端部监测点1(0.011 5，0.038)、热挡板后端监测点2(0.327 5，0.038)以及潜入式空腔内监测点3(0.366，0.05)处的振频与振幅进行了监测与计算。

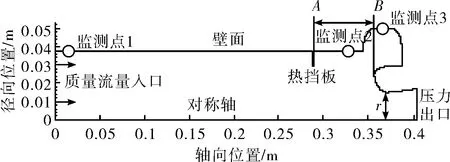
图1 计算模型

计算网格的划分在一定程度上可以影响计算结果的精度，苏万兴在文献[11]中研究了网格数目对计算结果的影响，得到了能够准确计算该模型所需的最佳网格数目，文中采取了与之相近的网格划分方法，网格数目约为14万。网格划分如图2所示。

图2 热挡板附近的网格划分

2 计算结果与分析

2.1 挡板高度对压力振荡特性影响

文献[11]研究了热挡板位置对发动机内的压力振荡的影响，发现合理设计热挡板位置可以降低压力振荡的幅度，较好的指导了热挡板的设计，但热挡板的高度对火箭发动机压力振荡影响规律不是很清楚，因此探讨挡板高度对发动机压力振荡特性的影响很有必要。为了更加直观的观察热挡板高度的改变对压力振荡的影响，在图1的基础上新增热挡板高度L为1 mm、3 mm 、5 mm、7 mm、11 mm的5组算例，其他条件与图1保持一致，并结合标准模型(图1L为9 mm)的计算结果，共6组算例进行对比分析。

首先分析不同算例的时均流场。图3显示了不同热挡板高度模型的速度流线图。可以清楚地看到，随着热挡板高度增加，回流区范围逐渐增大，涡的中心位置横坐标后移，纵坐标下移。

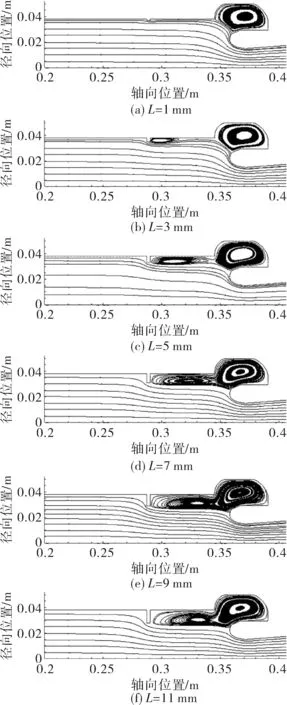
图3 不同热挡板高度模型的速度流线图

其次分析不同算例的涡量云图。图4显示了不同热挡板高度模型涡量云图。从云图对比图中可以清楚地看到，随着热挡板高度L的变大，平均涡量也随之变大，这意味着热挡板高度的增加使得障碍物旋涡脱落的强度增加；同时从涡量云图也可以看出漩涡在喷管前部的碰撞点位置下移，涡碰撞破裂后，一部分涡量进入潜入式喷管空腔内。

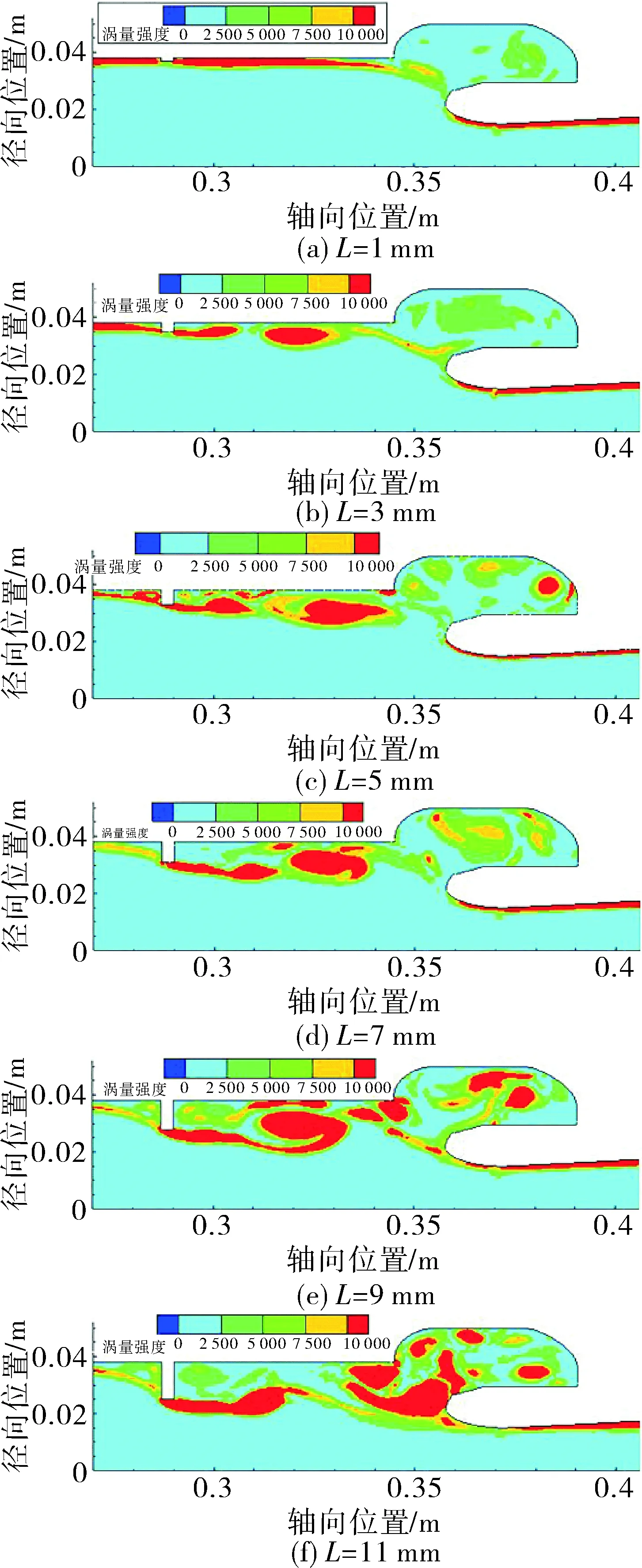
图4 不同热挡板高度模型的涡量云图

对不同热挡板高度算例监测点1处计算得到的压力数据进行处理分析，可以发现，随着热挡板高度的增大，不同工况下压力振荡无量纲幅度逐渐增大，由热挡板高度L=1 mm时的0.233%增长到L=11 mm时的1.6%，几乎增加了一个数量级，如图5所示。因此合理的挡板高度设计对减小压力振荡具有非常重要的意义。

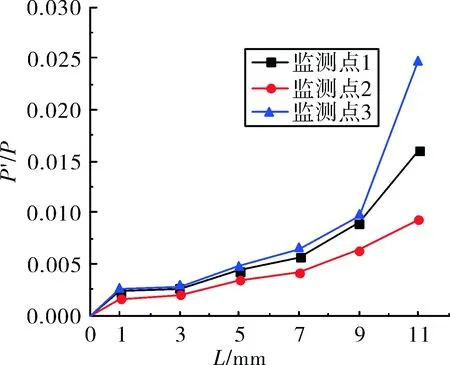
图5 不同热挡板高度下的压力振荡无量纲幅度

从图5也可以看出，3个监测点振幅大小顺序为监测点3>监测点1>监测点2。其中监测点2中压力振幅最小，这是由于监测点1和监测点3处于发动机声压的波腹处，对压力振荡敏感，监测点2处于发动机声压的波节与波腹之间，对压力振荡没有监测点1和监测点3处敏感；此外监测点3处的振荡幅度大于监测点1处，这是因为监测点3除了处于声压的波腹处外，还处于潜入式喷管的潜入式空腔内，潜入式空腔的加入会使得压力振幅增大。 Anthoine[4-5]通过理论计算及实验测试的方法研究验证了该结果。此外，随着热挡板高度的增加，监测点3与监测点1处的振荡幅度的差距逐渐增大，这从侧面也证实了流入潜入式喷管空腔内的涡量逐渐增多，较好的吻合了涡量云图的结果。

2.2 挡板弯曲角度对压力振荡特性影响

挡板形状设计也是分段装药设计的重要组成部分，因此合理设计热挡板非常重要，但是相关方面的研究不是很充分。以图1所示的基本模型为基础，新增热挡板弯曲角度(热挡板与发动机壁面的夹角)为30°、45°、60°、75°四组算例，图1所示模型的弯曲角度为90°，其他条件与图1保持一致，并结合标准模型的计算结果，进行对比分析。

首先分析不同算例的时均流场。图6显示了不同热挡板弯曲角度模型的时均流场。可以清楚地发现，随着热挡板弯曲角度α的增大，热挡板后缘下游回流区涡与潜入式空腔内部的涡结构联系更加紧密。热挡板上游附近形成的回流涡的范围逐渐变小，当α=90°时基本消失。

图6 不同热挡板弯曲角度模型的速度流线图

对不同工况下监测点1处的压力振荡数据进行处理分析，不同弯曲角度下监测点1处的无量纲压力振荡频谱图如图7所示。

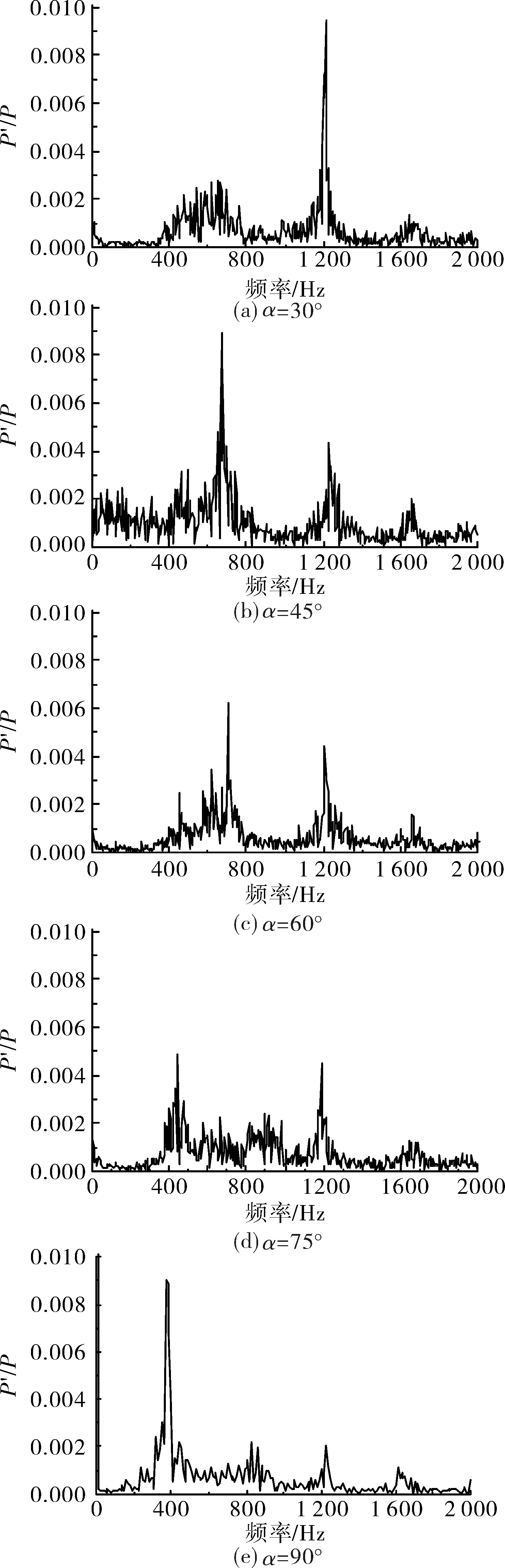
图7 不同热挡板弯曲角度下的压力频谱分布图

从图7可以看出，随着热挡板弯曲角度的增大，不同工况下压力振荡最激烈幅度处所对应的频率从高模态向低模态转移，且振荡现象逐渐从单一频率下剧烈的振荡向多频率振荡分散，降低了振荡幅度，这主要是因为热挡板的弯曲改变了声涡耦合的反馈路径，从而影响了涡脱落与声场之间的耦合。在弯曲角度为90°时完成了频率的转移过程，压力振荡最激烈处由三阶转移到了一阶，多频率振荡向基频振荡集中，压力振荡幅度再次增大。该结论较好的吻合了文献[13]中Jerome冷流试验得到的结论，因此合理的设计挡板弯曲角度可以把较大的单一频率下的压力振荡幅度分散为多个频率下较小的压力振荡幅度，从而降低单一频率下剧烈振荡对发动机的危害。