单通道旋转弹舵面控制律与转速研究*

杨 宇，温求遒，李 威，夏群利，阮 聪

(北京理工大学宇航学院， 北京 100081)

0 引言

在飞行器中，有一类绕自身纵轴进行旋转的导弹叫做旋转弹。通过弹体的旋转运动可有效改善推力偏心、质量偏心以及外形加工工艺误差等干扰的影响，保持弹体的稳定性[1]。旋转弹通常不控制滚转回路，根据舵控制方式，可分为单通道控制与双通道控制。双通道控制为两个舵机分别控制一对舵面，实现俯仰与偏航的控制飞行，与非滚转弹的俯仰偏航相对比，双通道旋转弹只是将自动驾驶仪生成的俯仰偏航舵指令通过当前滚转角分解到两对舵上去，在不考虑滚转带来的指令滞后情况下，双通道旋转弹与非旋转弹控制效果一样[2]。单通道控制则是旋转弹特有的控制方式，即以一个通道的控制器同时控制俯仰和偏航两个方向的运动。早期的单通道控制采用继电式舵机，通过弹体旋转一个周期内数次变换舵机指令，通过不同的变换时间点使得舵机在一个旋转周期内工作的积分效应产生等效控制力，最终实现弹体在空间内任意方向的控制飞行[3]。随着舵机的发展与性能改进，比例舵机应用愈发广泛，相对于继电式舵机，比例舵机可以自由控制当前舵机转动角度，能够更加自由的实现单通道舵机控制方式[4]。文中研究继电式舵机与比例舵机的不同的舵机控制方式并通过仿真分析其稳定控制条件。

1 制导火箭弹运动模型的建立

为方便分析旋转弹的舵面控制律，建立与弹体固联的弹体坐标系Ox1y1z1与不跟随弹体转动的准弹体坐标系Ox2y2z2。

弹体坐标系原点O为导弹质心，Ox1轴与弹体纵轴重合且指向头部为正，Oy1轴位于导弹纵向对称面内且与Ox1轴垂直，向上为正，Oz1轴与纵向对称面垂直且符合右手定则。

准弹体坐标系原点为导弹质心O，Ox2轴与弹体纵轴重合且指向头部为正，Oy2轴位于包含导弹纵向的铅垂平面内且与Ox2轴垂直，Oz2轴通过右手定则确定。坐标关系如图1所示[5]。

2 Bang-Bang舵控制律数学模型

Bang-Bang舵控制律采用的是继电式舵机控制，舵机只能为正或负的最大角度。因此，采用的控制方法是在一个控制周期内不断的变换舵片的极性以实现对导弹空间内任意运动方向的控制[6]。现设偏航指令为σ1，俯仰指令为σ2。Bang-Bang舵在一个周期内方向变换两次，设两次变换方向的时间分别是φ和π+θ，指令如下：

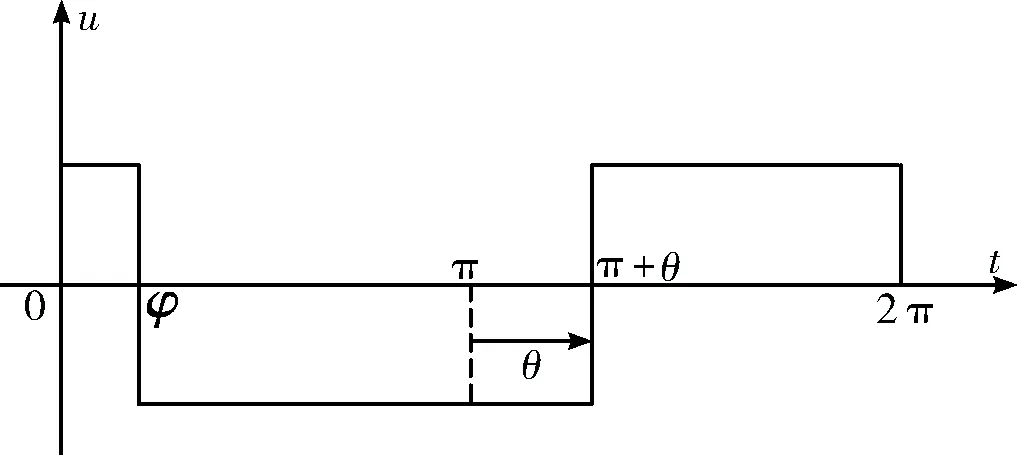
图2 Bang-Bang舵指令变换曲线

将舵指令分别投影到准弹体坐标系下的Oy2轴与Oz2轴，投影曲线如图3所示。

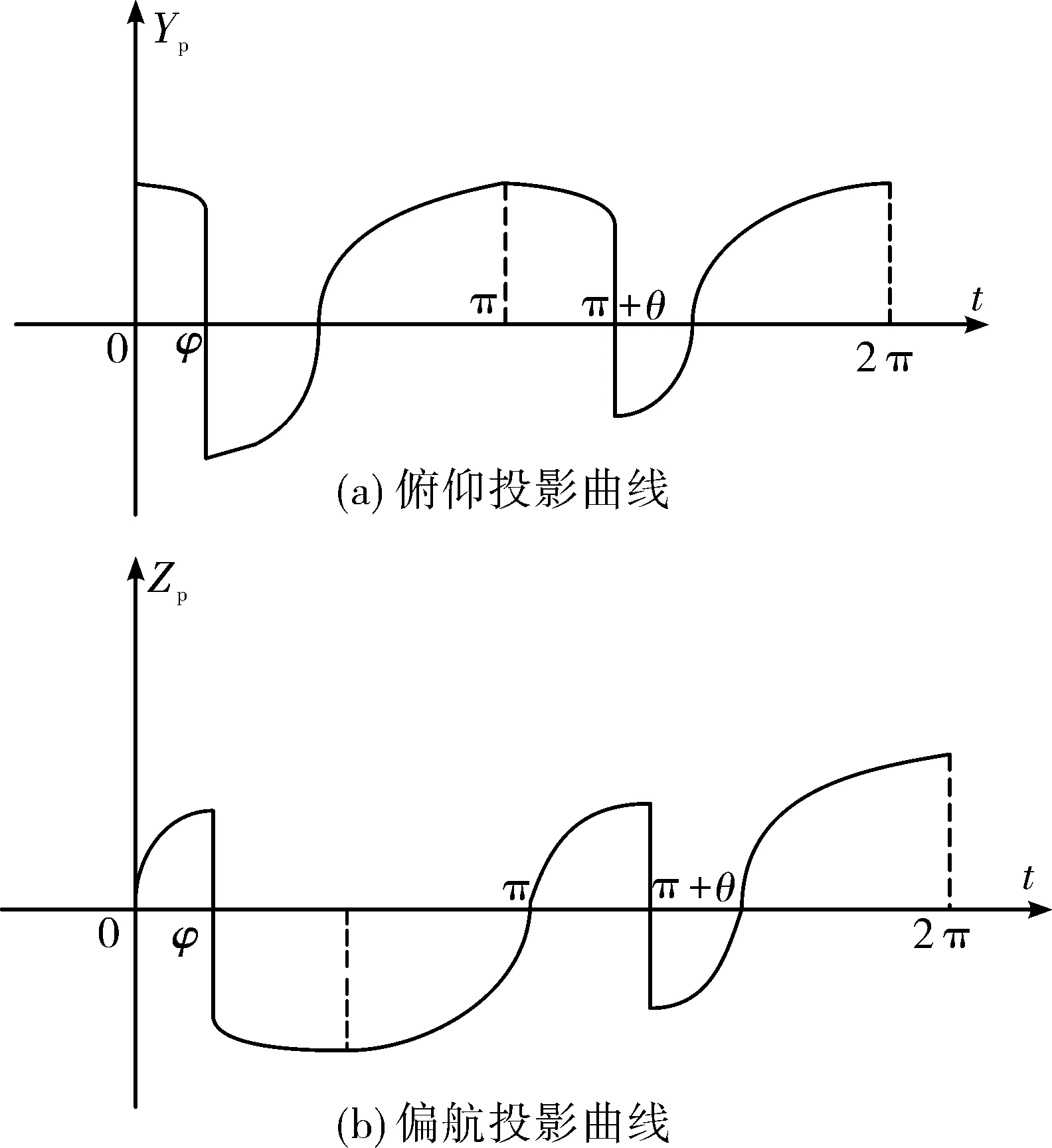
图3 Bang-Bang舵指令俯仰偏航投影曲线

根据单通道旋转弹一个舵指令周期在俯仰偏航方向的积分效果要等效于该段时间内弹体指令作用效果，可以得到以下公式：

(1)

对式(1)求解，可得出：

(2)

上式即为Bang-Bang舵进行控制时两次变换的时间点，通过指令以及最大舵偏角求出变换时间。

3 正弦舵控制律数学模型

旋转弹舵控指令控制周期设为1 Hz，即每一个旋转周期，控制指令也为一个周期变换，设偏航指令为σ1，俯仰指令为σ2，弹体转速为w，舵指令幅值为Δ，初始相位为φ，弹体旋转一周时间为T，正弦舵指令为：

delta(t)=Δsin(wt+φ)

(3)

当前指令的控制要求正弦舵在俯仰和偏航方向上的积分效应为指令持续一个旋转周期的效应，根据以上要求，可以得出：

(4)

对式(4)求解得到舵控信号的幅值和初始相位：

(5)

正弦舵舵指令原理可解释为首先将俯仰与偏航舵指令合成一个铅垂面的合指令，舵机旋转一周在该合指令方向积分值最大，在与该合指令垂直方向为0。为实现弹体平均产生的过载方向沿着该合指令方向，合成过载大小可表示为sqrt(σ1·σ1+σ2·σ2)，为达到指令要求，则要求当弹体转到合成过载方向，舵指令为最大，舵指令转动到与合成过载垂直的方向则舵指令为0[7]。如图4所示。

图4 正弦舵指令示意图

4 控制稳定性研究与仿真分析

单通道控制依托舵面在弹体旋转一圈的情况下作用的积分效应，当弹体转速过慢时，弹体几乎能够完全的响应每一个时刻舵指令，无法满足舵控指令的积分效应。因此，单通道旋转弹的转速必须高于一定的数值来满足控制需求。现以比例舵控制律分析弹体的最低转速需求。

4.1 仿真条件

为分析不同舵面控制律的控制效果与单通道控制所需的最低转速要求，通过某鸭舵控制的旋转火箭弹进行分析，该火箭弹飞行时间约为40 s，主动段推力持续时间2.3 s。选取飞行时间为20 s时，在该时间点给出一个准弹体系下阶跃舵指令，令火箭弹转速为0，给出一个恒定舵面偏转角度，得到当前状态下火箭弹的阶跃响应。设置火箭弹不同的转速，准弹体系下的阶跃指令保持不变，分析单通道旋转弹舵面控制律的控制效果并对火箭弹控制需求转速进行研究。20 s时弹体状态如表1所示。

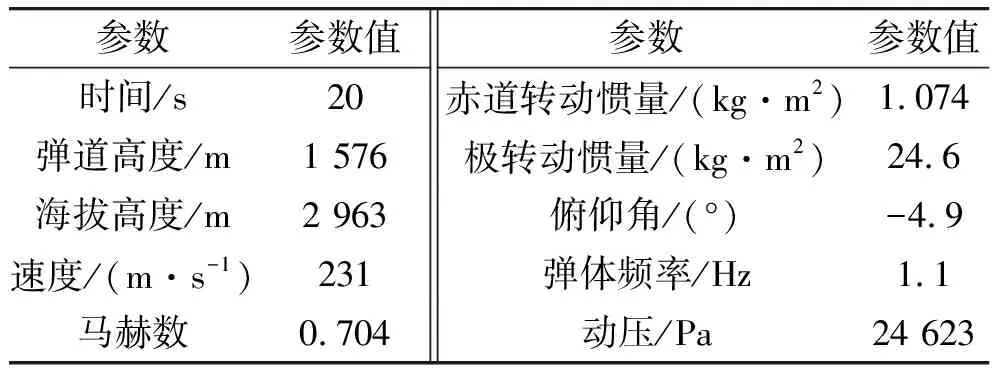
表1 仿真条件

4.2 正弦舵控制律推导

设转速为0，在20 s给出2°的恒定俯仰舵指令，当转速为2 Hz时，舵面实际角度如图5所示。

图5 正弦舵舵面转动角度曲线

将舵效分解到俯仰方向与偏航方向可得见图6。

图6 正弦舵指令等效俯仰偏航指令

从上图可以看出等效俯仰舵指令为0至4°周期变化的正弦指令，其积分效果与不滚转时2°俯仰指令作用效果相同。偏航指令为赋值幅值2°的正弦指令，积分效果为0，说明正弦舵控制律能够有效的响应俯仰偏航指令。

4.3 正弦舵指令响应仿真

设弹体不滚转，给出俯仰2°舵指令，则角速度及过载响应如图7所示。

图7 非滚转弹体角速度与过载响应

分别设置弹体转速为1 Hz、3 Hz、5 Hz，通过上述的公式采用正弦舵控制律，弹体过载和角速度响应如图8所示。

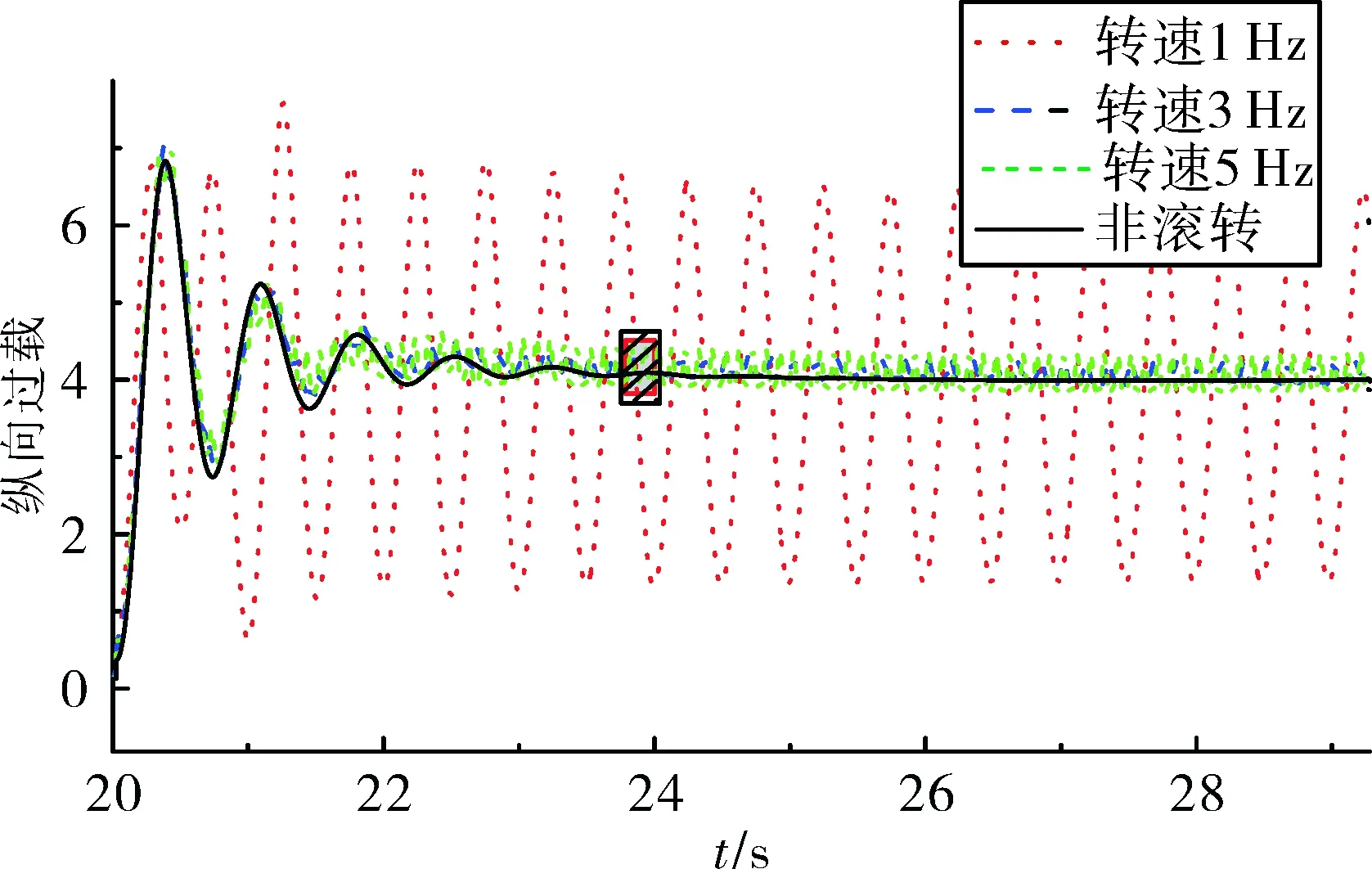
图8 不同转速弹体过载响应

图8中黑框放大图如图9所示。

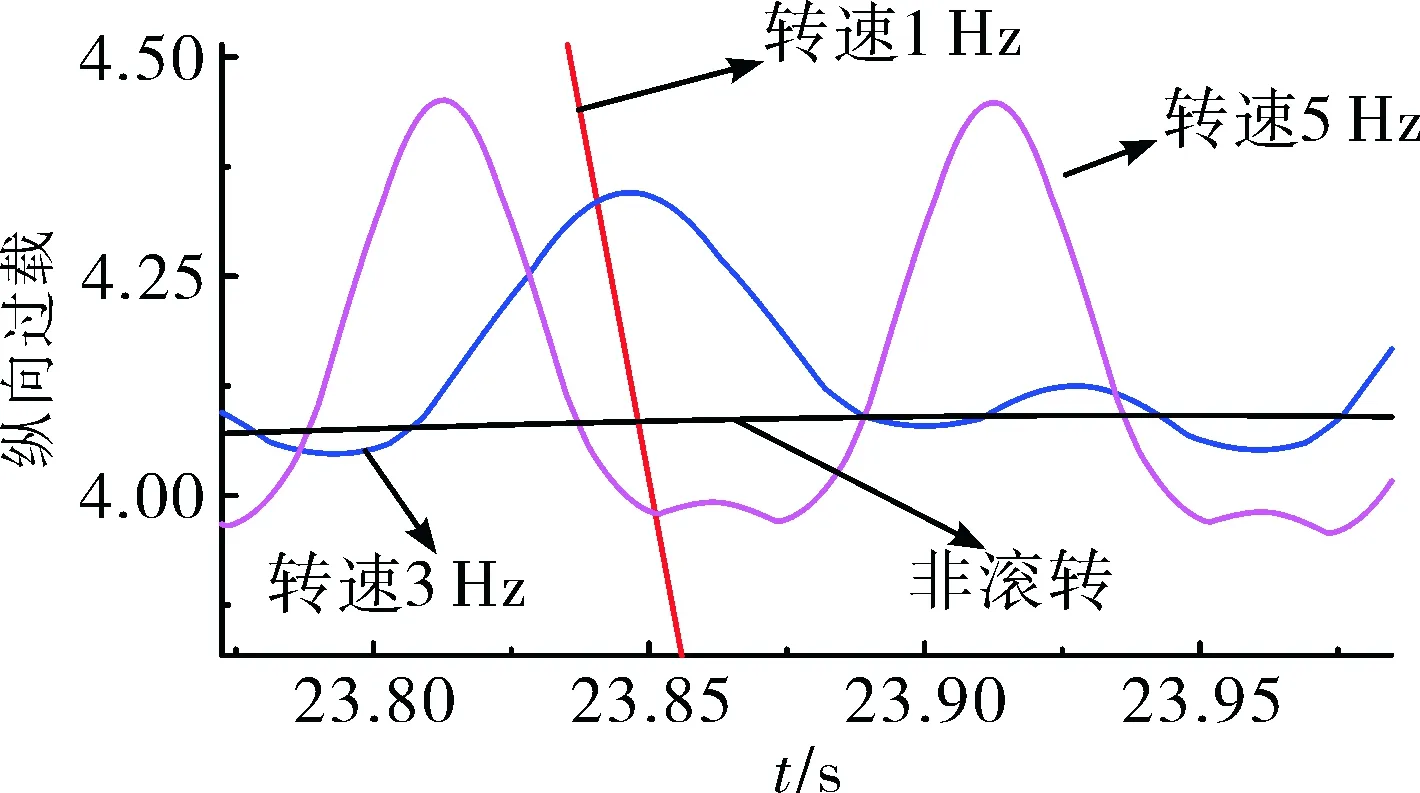
图9 过载响应放大图

从图9可以看出，转速为1 Hz时，弹体几乎无法正确响应过载指令，当转速提高到3 Hz以上时，弹体俯仰过载与非滚转时响应情况很接近，说明单通道控制无法在低转速时使用。偏航响应与俯仰相类似，不再进行说明。

在弹体的阶跃响应过程中，弹体角速度可以作为响应品质的一个评判，角速度超调量越小，响应稳定后角速度振幅越小说明响应品质越好[8]。同样条件角速度响应如图10所示。

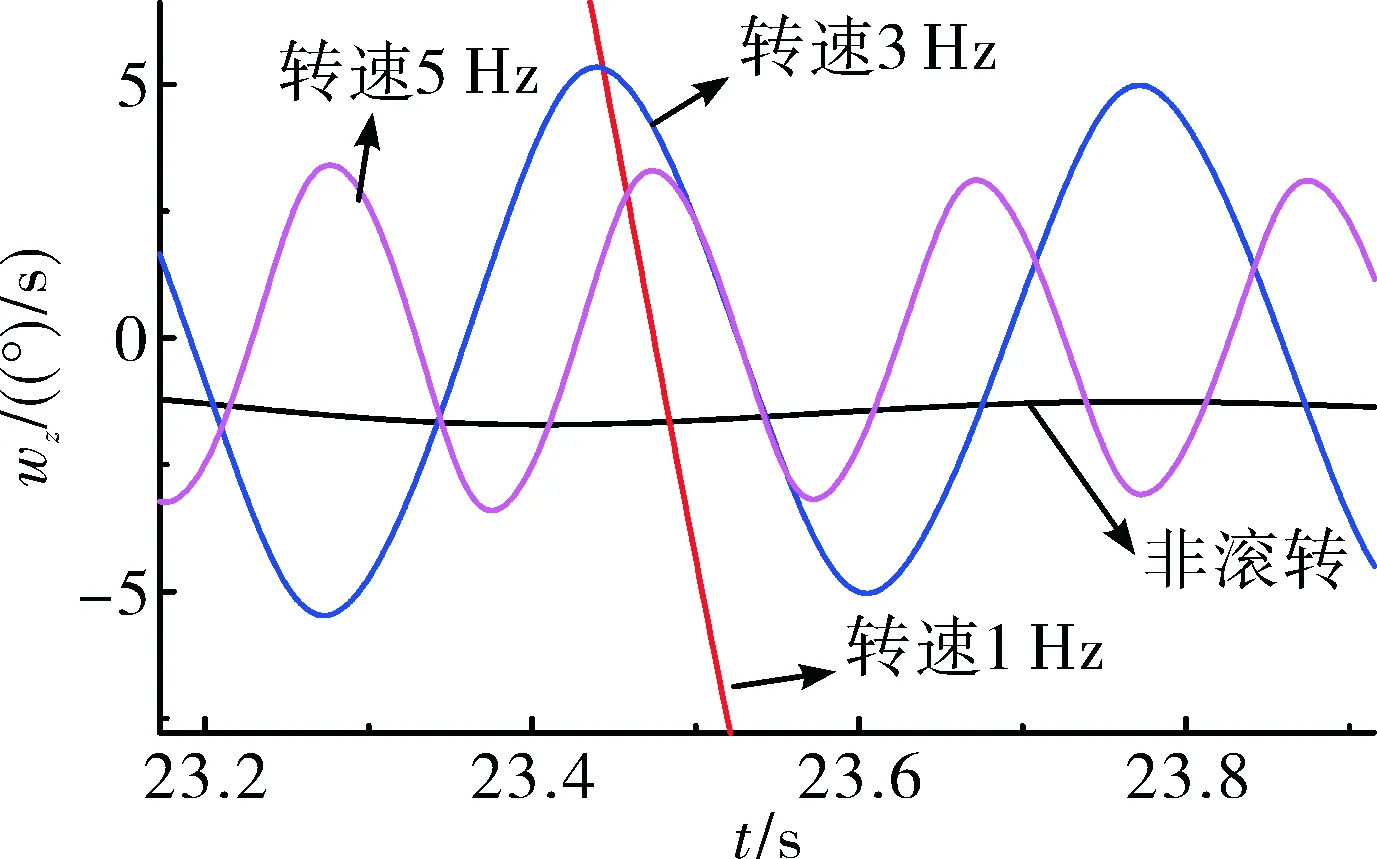
图10 2 Hz弹体频率角速度响应放大图

从图10可以看出，当弹体转速为1 Hz时，俯仰角速度全程都在振荡，没有收敛趋势，随着转速提高到3 Hz以上，俯仰角速度能够收敛在一定范围内振荡，弹体转速越高，角速度振荡范围越小。现取不同转速，并记录稳定响应的角速度幅值，曲线如图11所示。

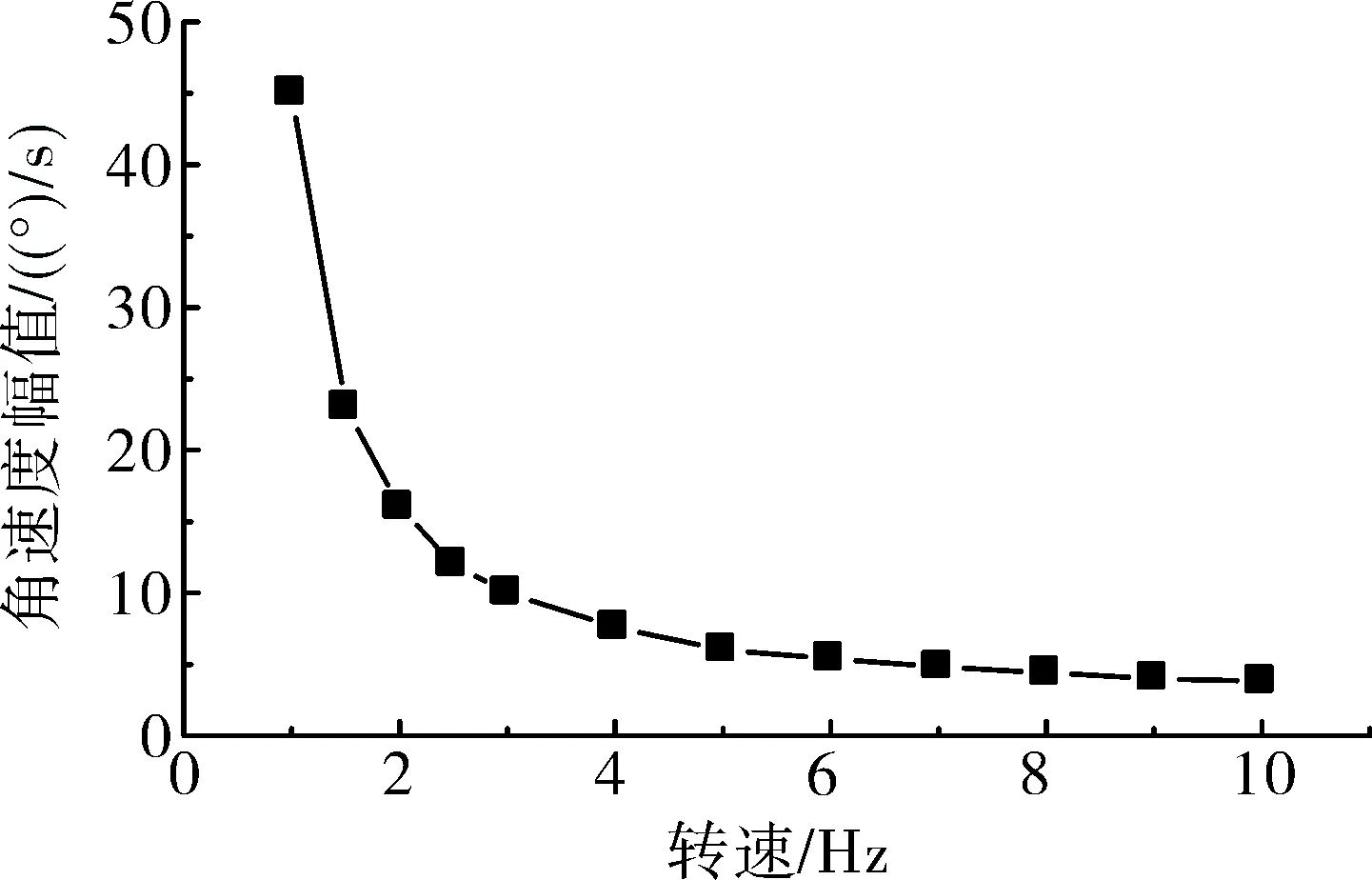
图11 1 Hz弹体频率不同转速角速度幅值曲线

根据图11可知，当转速小于3 Hz时，弹体俯仰角速度振荡幅值较大，且随着转速提高角速度幅值快速下降。当转速大于4 Hz的时候，角速度幅值同样随转速提高而下降，但下降的幅度较小，变化较为缓慢，结合图8、图9可知，当转速大于3～4 Hz时，单通道舵面能够有效的工作。

4.4 仿真分析

根据飞行力学可知，弹体环节可以简化为二阶环节，二阶振荡环节与阶跃响应的响应时间和弹体频率有直接关系，弹体频率越高，响应速度越快[9]，响应速度过快会导致弹体在一个旋转周期内快速跟踪每一个时刻的指令，体现不出舵机的控制效果。根据图11可知，当前仿真状态弹体频率为1 Hz，通过弹体不同转速的角速度幅值与过载响应判断，当转速为3 Hz以上时，可通过单通道控制方法对旋转弹进行有效控制，现通过改变弹体质心位置改变导弹的弹体频率，将弹体频率增大至2 Hz。不同转速的角速度响应如图12所示。

图12 2 Hz弹体频率不同转速角速度幅值曲线

改变弹体频率后，当转速达到6 Hz以上时，角速度幅值变化幅度较小，达到稳定控制的目的。此时弹体频率为2 Hz，说明单通道控制需要满足转速至少达到弹体频率3倍以上。

5 结论

文中对单通道旋转弹的舵面控制律进行了分析，建立了Bang-Bang舵与正弦舵的数学模型并推导解析公式。将得到的数学模型应用到实际工程中，对单通道旋转弹进行阶跃指令响应分析，仿真表明两种舵面控制律能够有效的实现单通道控制。同时对能够稳定控制的弹体转速进行了研究，通过对阶跃指令响应的数学仿真，证明了单通道控制要求弹体转速需大于3倍的弹体频率。