一种单孔径毫米波单脉冲雷达前视三维SAR成像算法*

李小雷，蔡 雨，袁 军，刘平安，王 力，刘 颖

(1 西安现代控制技术研究所， 西安 710065； 2 北京机科国创轻量化科学研究院， 北京 100083)

0 引言

在民用和军事领域获得被观察区的三维高分辨率雷达图像具有广泛的应用前景。但目前主要技术手段需要依赖雷达平台与目标方位向相对运动所导致的多普勒频率展宽来提高方位分辨率，包括多普勒波束锐化技术(DBS)和合成孔径技术(SAR)等。当波束覆盖飞行路线正前方区域时，被观察区域的地面目标回波多普勒带宽基本为零，而DBS和SAR不具备高分辨率成像的能力，形成前视盲区。

近年来，国内外研究人员提出了多种实现运动平台雷达前视高分辨率成像的方法，如前视SAR[1-3]、单脉冲前视成像[4]与多通道解卷积[5]等。前视SAR方位向的分辨率受切航线天线阵列长度制约，系统实现比较复杂；在波束内存在多个目标时单脉冲前视成像技术的性能会急剧恶化；单通道解卷积技术对加性噪声非常敏感，重构结果不连续依赖于测量数据，表现出固有的病态特性,多通道解卷积技术同样面临解卷积后的信噪比损失问题，处理过程复杂。

针对雷达前视探测所面临的技术问题，文中借鉴前视SAR技术，在方位通过虚拟合成阵列，运用逆散射方法对散射中心方位分布进行估计，再通过多普勒处理与单脉冲测角实现了单天线雷达的方位高分辨成像，在俯仰面内通过结合转台成像原理并结合多普勒分析与单脉冲测角实现了俯仰高分辨成像。最后通过距离-方位像和距离-俯仰像可以合成三维雷达像。文中方法对雷达运动轨迹无特殊要求，实时性较强，可实现前视条件下对目标的三维成像，兼具较高的学术价值和工程应用价值。

1 成像原理

前视SAR成像过程中雷达平台的运动方向与距离向一致，与方位和俯仰向垂直。图1给出了前视SAR 的成像几何配置图，x轴表示距离向，y轴表示方位向。雷达平台在离地面高度为H的航线上沿x轴方向以速度v运动。

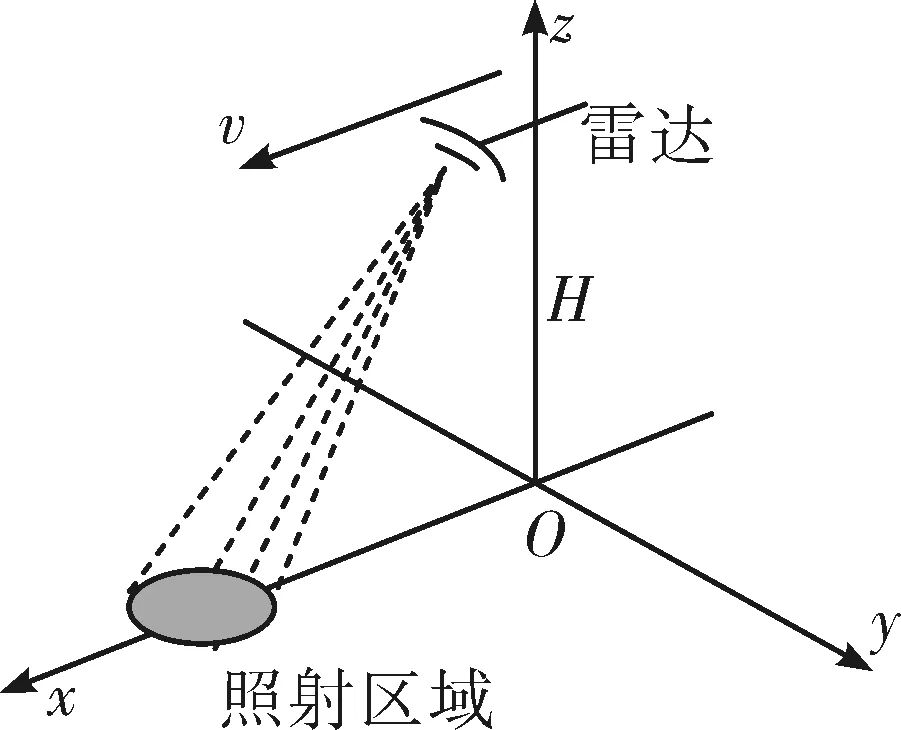
图1 前视SAR成像几何配置

图2 方位面内的虚拟天线阵列

在运动过程中，由于雷达前视正前方目标区域，目标区域中散射点的雷达回波中方位向不存在多普勒效应，这些点无法用多普勒分析进行分离，理论上无法实现方位高分辨。但如果假设在方位面内与雷达运动方向垂直的方向上存在一系列以一定间隔布置的接收天线，这些天线以一定的时序间隔(切换时间)依次接收雷达回波，则相当于雷达沿y轴运动，在不同特定位置上以一定斜视角观察目标区域，形成虚拟的合成孔径，从而实现方位高分辨。当雷达以高的脉冲重复频率发射宽带信号，为了保证发射脉冲与虚拟的天线接收回波相匹配，信号来回双程所用的时间应与虚拟接收天线工作切换时间一致，如果切换速率是vs，则相当于真实接收天线在方位向以同样的速度运动[1]。在方位向形成以一种虚拟线性阵列为长度的合成孔径，可提高方位向分辨率。

方位面内，首先通过逆散射法估计出目标区内的强散射点分布，然后合成方位线阵上各接收天线依次接收一遍后得到的回波数据并按距离进行方位多普勒分析，将同一距离单元内的强散射点进行分离后可获得距离-多普勒图像，然后通过单脉冲比幅测角可生成目标的距离-方位角度像。

俯仰面内，由于雷达平台有一定的飞行高度，在平台向前飞行过程中相当于对成像区域形成一定的转角，经过一段时间积累后，也可依据ISAR原理进行距离-多普勒成像，然后同方位成像一样生成目标角度像。

2 成像算法

2.1 虚拟方位线阵回波信号估计

设雷达系统为单发单收系统，当目标区域未知且分布有多散射中心时，如何根据单一的实际接收信号虚拟出线阵上任意口径上的接收信号成为方位上实现高分辨的前提，这里将采用一种电磁逆散射方法——矩量法求解目标区域内强散射中心的方位分布。

图3 散射中心估计原理

根据电磁散射理论，对于任意散射体，其周围的总场E(r)总等于入射场Ei(r)与散射场Es(r)之和，即

E(r)=Ei(r)+Es(r)

(1)

对未知区域成像可归结为已知散射场(回波)，求解散射中心位置问题，即是一个逆散射问题。对于宽带雷达，当雷达通过脉冲压缩在距离上检测到目标时，可以沿相应距离单元将雷达波束均分为n份，n值由所需的方位分辨率决定，若距离向单元个数为m，则目标区域可以被分为m×n个单元，如图3所示，设每个单元中只存在单一的合成散射中心，则接下来的问题可以归结为求解这m×n个单元的散射系数。这个问题可以通过矩量法求解，经过推导，经典的电磁场积分方程可以重新表示为以下形式[6]：

GE=Es

(2)

矩阵G中对角线元素表达式变为：

(3)

非对角线矩阵元素表达式为：

(4)

以上两式中，xp、xq分别表示坐标x、y的值，k0为自由空间电磁波波数，ω表示角频率，μ0、ε0分别为自由空间磁导率和介电常数，相关参量表达式如下：

τ(r)=σ(r)+jω[ε(r)-ε0]

αmn=k0Rmn，Rmn=|rm-rn|

其中，Rmn表示第m、n个散射中心之间的距离，σ为介质电导率。将强散射中心等效为半径为rn的球，则散射中心体积Δv可由下式进行估算。

方程(2)为N×N阶矩阵方程(N=m×n)， 该方程可以根据实际单天线接收的回波计算各个散射单元内的散射系数，即强散射中心分布情况，具体方法为直接提取那些过门限的散射系数所对应的单元编号及其坐标，应用该方法实际处理时，由于该方法计算量为O(N2)，为降低计算量，需要进行降维处理，可按距离单元进行方位处理，即以任一距离单元的子脉冲为激励，求解该距离单元内的散射点方位分布，这样可以将求解大规模稠密矩阵问题转化为求解多个小规模稠密矩阵问题。

设估计的散射单元个数为F，雷达信号形式为线性调频信号，雷达第n个接收天线的空间位置坐标为(xn,yn,H),目标区域内任意散射中心p的坐标为(xp,yp,zp)，令其发射路程为Rt,n，则任意虚拟阵元n位置处的接收信号为

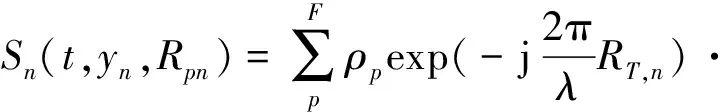
(5)

式中ρp为散射点p的后向散射系数；

沿线阵依次生成Sn(t,yn,Rm)信号后，该序列信号可用于方位向聚焦或非聚焦处理。

2.2 三维像的生成

用宽带信号可以得到高的纵向分辨率，使不同纵向位置的散射点分置在各个距离单元里；然后用多普勒分析将横向位置不同的散射点分离形成多普勒像，再用差波束对各个散射点逐个单脉冲测角，从而得到以距离-角差作为成像平面[7]的雷达图像。

对回波FFT进行距离脉压并进行相位补偿后信号为

(6)

方位直接傅里叶变换即可得到目标像

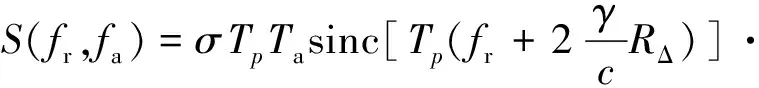
(7)

式中:Tp为发射信号时宽；γ为调频率；Ta=N/PRF为方位积累时间；N为方位脉冲个数；PRF为方位采样频率；fr为快时间频率，fa为方位多普勒频率；c为光速；ys为方位数据录取期间雷达与目标间在方位向的虚拟相对位移量，等于天线切换速度vs与数据录取时间的乘积。

对同一距离单元散射点进行多普勒分离后,在和差信号成像基础上采用像素点比幅法测角, 最后完成散射点定标及成像，比幅可以完成垂直于距离向的定标, 将散射点多普勒转化为实际距离。仍以方位向处理为例，其测角方法为

(8)

式中Kθ为比幅的比例系数。

同理，俯仰面内根据转台模型，也可直接傅里叶变换得到目标俯仰多普勒像，然后通过测角完成俯仰定标。最后，可通过距离-方位像与距离-俯仰像合成三维像。

3 仿真与试验结果

3.1 散射点方位分布估计算法仿真

由于方位向虚拟合成孔径回波模拟的有效性对方位成像极为重要，因此首先对基于逆散射方法的散射点方位分布估计算法的有效性进行了仿真验证。设雷达工作在W波段，波束宽度为1.5o，首先设波束被均分为30份，沿方位向有9个散射强度不同的散射点分布于波束内，这9个散射点分布于同一距离单元上，仿真结果如图4所示，通过图4可以发现，这9个散射点的方位分布被准确的估计出来。

进一步提高方位分辨率，波束被均分为90份，某一距离单元内有10个散射点分布于不同单元内。散射点方位分布情况如下，有5个散射点分布在第10～25个方位单元内，有3个分布在第40～50个方位单元内，还有两个分布在第60～70个方位单元内，通过图5可以发现，文中逆散射方法也可以准确估计这些散射点的方位分布。

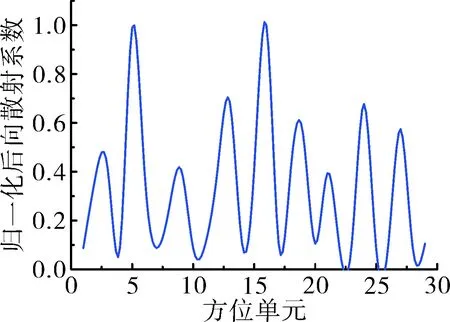
图4 波束被均分30份时方位分辨率仿真结果

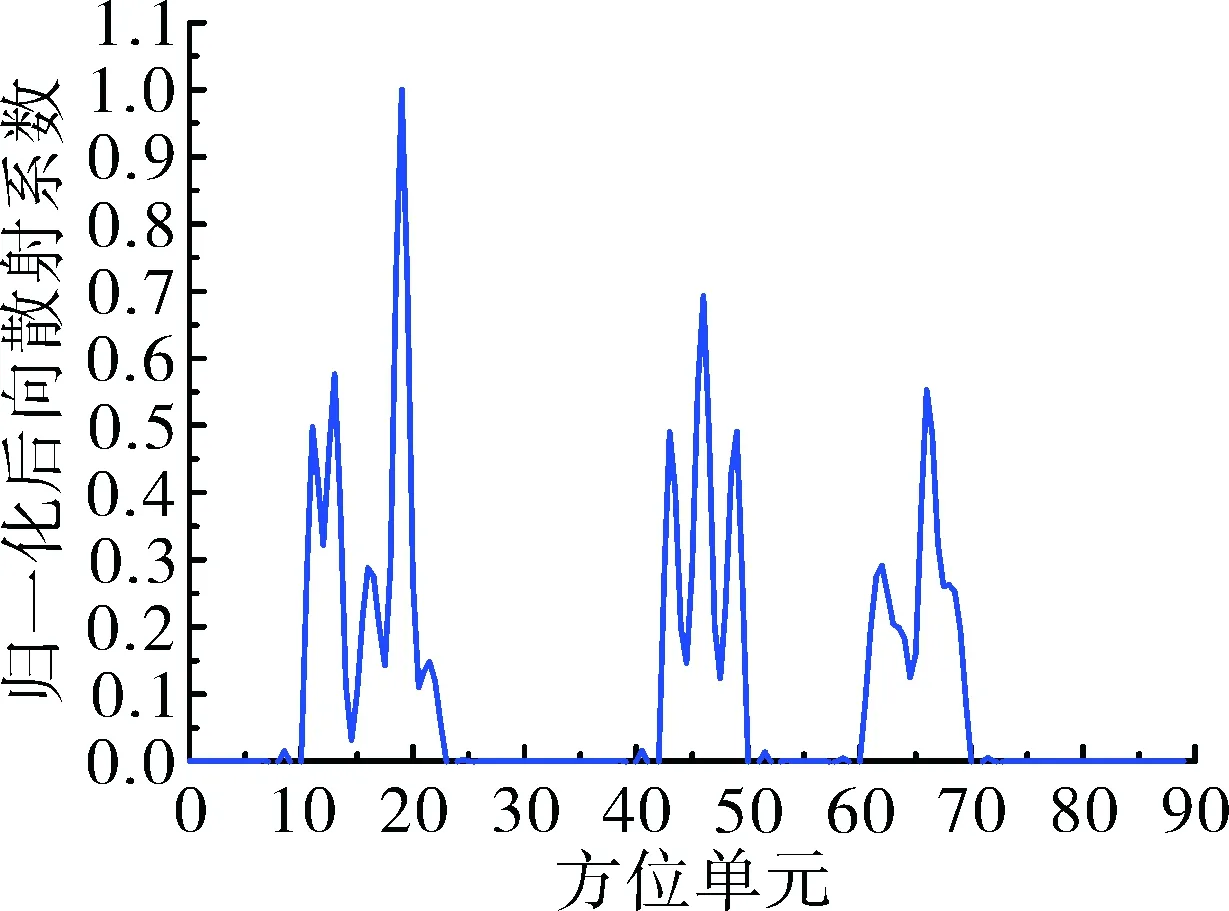
图5 波束被均分90份时方位分辨率仿真结果

3.2 成像仿真

在进行三维成像仿真时，首先建立了坦克三维电磁仿真几何模型，然后应用物理光学法仿真了坦克上散射中心的分布并生成目标回波，对回波成像处理的结果如图6所示。仿真所用参数为：雷达带宽500 MHz，脉冲宽度100 ns，脉冲重复频率20 kHz，雷达速度330 m/s，雷达飞行高度200 m，波束宽度1.5°，波束方位分辨率0.015°(划分为100等份)，雷达与目标相距2 500 m，成像积累时间0.5 s，雷达航迹正对目标。

从成像结果看，目标的轮廓较为清晰，距离、方位、俯仰维的分辨率均优于0.7 m，能够通过成像结果估算目标的三维尺寸。

3.3 实测数据成像处理结果

对文中方法还用实测飞行数据进行了验证，试验时W波段毫米波单脉冲雷达采用直升机系留飞行，所采用的目标1与目标2均为国外特种地面车辆的全尺寸模型，这些模型均可全方位模拟真实目标的雷达特性，飞行时雷达载机正对目标迎头飞行，如图7所示。

实测数据处理时所用参数为，雷达带宽500 MHz，脉冲宽度100 ns，脉冲重复频率20 kHz，雷达载机平飞速度为60 m/s，雷达载机飞行高度180 m，波束宽度1.5°，波束方位同样划分为100等份，雷达与目标相距1 800 m，成像积累时间为3.5 s。

对实测数据的成像结果如图8所示，从成像结果看，无论是目标1还是目标2，实测数据成像结果中目标外形三维轮廓均较为清晰，三个维度的分辨率同样均为0.7 m左右。

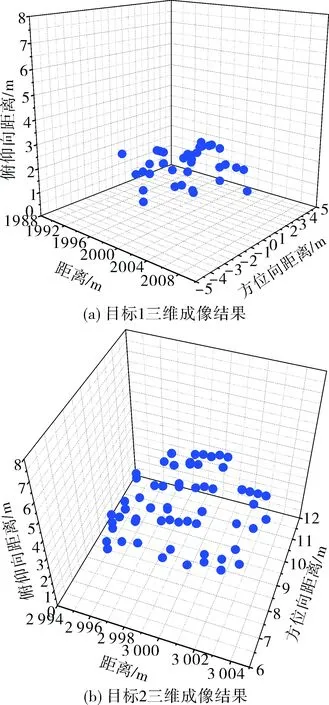
图8 三维成像实测数据处理结果

4 结束语

文中讨论的方法可以实现单孔径单脉冲雷达的高分辨率近实时前视三维成像，这在实际工程中具有广泛的应用前景。目前该方法主要存在两个问题，一是方位散射点分布估计时逆散射方法的运算量问题；二是成像积累时间问题。这两点是导致目前成像时间仍显较长的主要原因，后续需要从这两方面着眼进一步研究提高该算法实时性的方法，以扩展该方法的应用领域。