模式耦合快速求逆稀疏贝叶斯MIMO雷达成像*

2019-11-13胡仁荣童宁宁何兴宇

弹箭与制导学报 2019年3期

关键词：贝叶斯坐标系耦合

胡仁荣，童宁宁，何兴宇，陈桥

(空军工程大学防空反导学院，西安 710051)

0 引言

MIMO雷达成像目标回波信号通常表现出稀疏性。压缩感知技术能在欠采样条件下恢复稀疏信号

y=Ax+w

(1)

A∈RM×N(M≪N)为采样矩阵，x表示N维稀疏信号，w表示噪声，其均值为0，方差为σ2。然而在许多的MIMO雷达成像场景中，目标回波稀疏信号在距离维和方位维都会表现出连续性结构[1]。因此大量算法被提出来研究块稀疏信号恢复问题，比如Block-OMP[2]、混合l2/l1范数最小化[3]、模式耦合稀疏贝叶斯学习(pattern-coupled sparse bayesian learning, PCSBL)[4]等。前两类算法需要先验获取目标块结构信息，后者通过系数耦合的方法在不需要先验信息的情况下能够有效灵活的获取潜在的块结构信息。但其主要的缺点是每次的迭代都要计算复杂矩阵逆运算，随着信号维数的增加，计算量越来越大，从而很难应用到实际场景中。文献[5]提出了快速求逆稀疏贝叶斯算法，其方法是找到一个松弛明显下界，利用该方法，能将迭代过程中复杂矩阵求逆转化为对角矩阵求逆，从而大大降低运算量。

文中将模式耦合稀疏贝叶斯算法与快速求逆稀疏贝叶斯算法结合，提出基于模式耦合快速求逆稀疏贝叶斯(pattern-coupled fast inverse-free sparse bayesian learning, PC-IFSBL)算法，并将其应用到MIMO雷达成像中，该算法在降低运行时间的同时实现了块稀疏信号高效恢复。

1 MIMO雷达线阵收发分置回波信号模型

文中采用收发分置的MIMO雷达线形阵列建立信号模型，其结构如图1所示。发射阵列和接收阵列分别为It个发射阵元和Mr个接收阵元组成的均匀线阵，阵元间距分别为dt和dr。以第一个发射阵元为坐标原点建立三维坐标系，令收发阵列所在平面为X-Y平面，发射线阵为Y轴。分别用Ti和Rm表示第i个发射阵元和第m个接收阵元所在位置，坐标原点为T0。

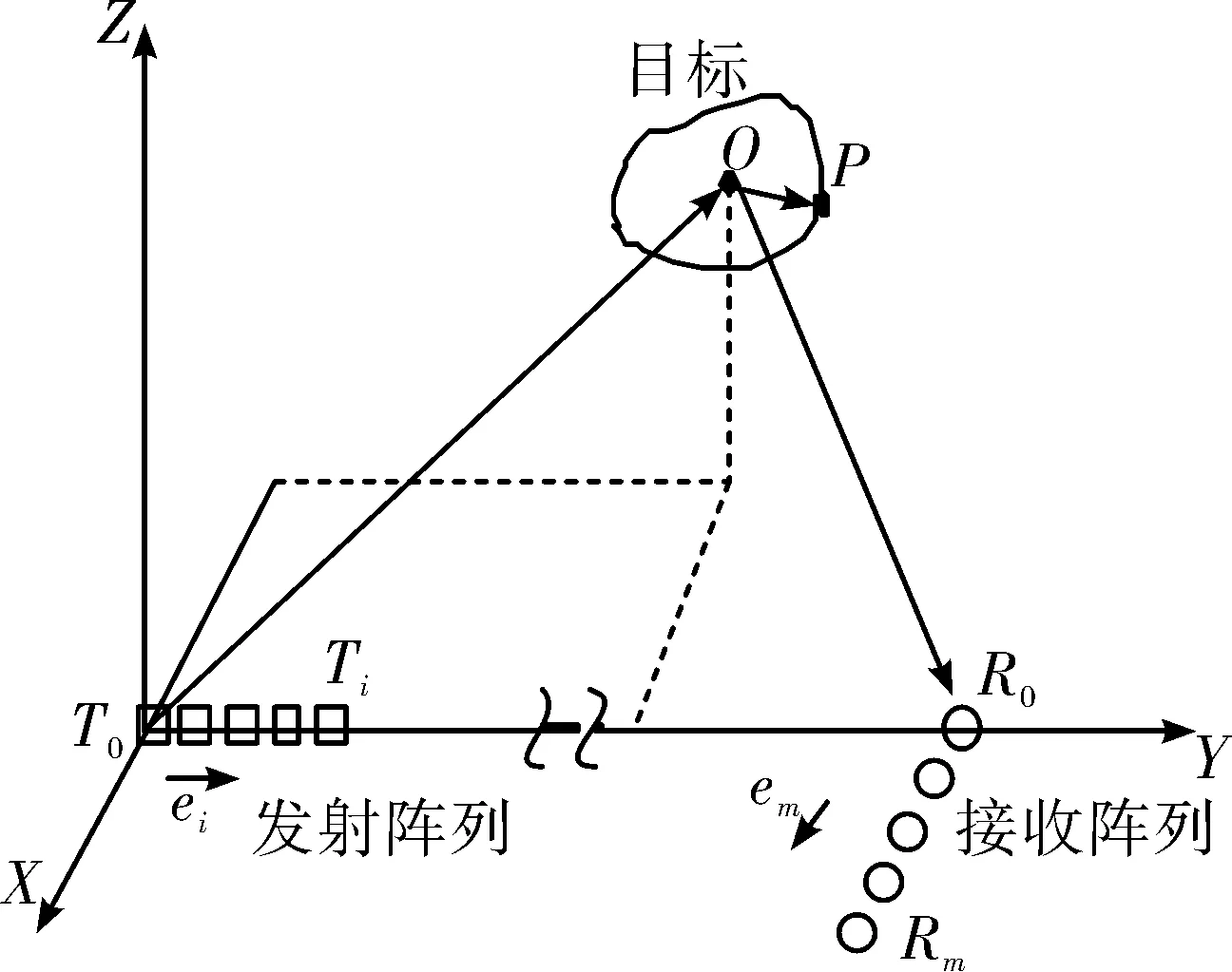
图1 收发分置MIMO雷达阵列模型

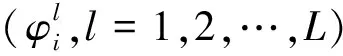
(2)

式中：fc为载波频率，T表示子脉冲长度，且发射信号STi(t)满足

(3)

在匹配滤波之后，第i个发射阵元的发射信号经目标上的散射中心p散射后被第m个接收阵元接收的回波信号为

(4)

式中：αi(t)是发射波形的自相关函数，τp,i,m=(TiP+PRm)/c是回波延时，TiP和PRm分别表示第i个发射阵元和第m个接收阵元到散射中心P的距离，c为波速。

假设目标上的任意一点为参考点O，且指定O为相对坐标系的原点，那么P点在该相对坐标系中的坐标为(Px,Py)，且相对坐标(Px,Py)不随目标的平动而变化。雷达的发射信号为窄带信号波形时，低距离分辨率可以保证不同接收阵元接收到的不同发射阵元的信号主瓣在一个距离分辨单元中，因此式(4)可近似为

(5)

式中λ为发射信号的波长。以参考点O为相位中心，则相位补偿后回波信号可表示为

(6)

根据文献[7]的引理和文献[8]中的近似，最终可得到包含D个散射中心的目标回波信号为

(7)

式中:σp=ζp(-j2π(OP)T(T0O/T0O+OR0/OR0)/λ)，(xp,yp)为包含目标散射中心P的位置信息(Px,Py)的位置参数。

2 模式耦合快速求逆稀疏贝叶斯算法

2.1 模式耦合稀疏贝叶斯模型

文献[4]提出了一种基于模式耦合稀疏贝叶斯分层模型，这种模型下x服从高斯先验分布

(8)

式中：

(9)

假定α0=0，αn+1=0对应端点x1和xn。β为系数xi与其相邻系数xi+1和xi-1之间相关性的参数，其中0≤β≤1。通过β将相邻系数的超参数联系到一起，实现块稀疏信号的精确重构。

根据传统稀疏贝叶斯学习，使用伽马分布作为超参数{αi}的超先验

(10)

式中参数a,b的选择在文献[4]中已经给出。

假设噪声方差已知，通过贝叶斯推理，得到信号x的后验分布为:

p(x|α,y)∝p(x|α)p(y|x)

(11)

式中p(x|α)由式(8)给出，而

(12)

显然，p(x|α,y)服从高斯分布，其均值和方差为:

(13)

式中:D为对角矩阵，其第i个对角元素为(αi+βαi+1+βαi-1)。

文献[4]利用期望最大化(expectation-maximization，EM)算法[9]实现了超参数{αi}的估计。则信号x的最大后验估计就等于它的后验分布的均值μ，即

(14)

综上可以看出，每次迭代更新计算均值μ时，都涉及到N×N维矩阵逆运算。

2.2 快速求逆稀疏贝叶斯模型

(15)

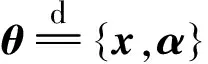
(16)

结合模式耦合稀疏贝叶斯联合参数估计思想，令Λ的第i个分量Λi=αi+βαi+1+βαi-1，通过β将相邻参数联系起来，从而得到基于快速求逆模式耦合稀疏贝叶斯(pattern-coupled fast inverse-free sparse bayesian learning, PC-IFSBL)算法进行计算更新。

若获取到超参数{αi}，则信号x的最大后验估计就等于它的后验分布的均值μ，即

x=μ

(17)

归纳上述分析过程，得出基于PC-IFSBL算法的MIMO雷达成像步骤为：

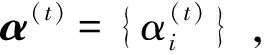
2)根据超参数α(t+1)计算式(16),根据式(17)得到新估计的雷达信号x(t+1)；

4)根据估计的雷达信号重构出目标像。

3 仿真与结果分析

仿真目标为波音747点散射模型，如图2所示，机长18 m、翼展16 m，由300个散射中心点组成，目标散射中心的散射系数随机设置，以发射阵列第一个阵元T0作为测量坐标系的坐标原点，以参考相位中心点O为相对坐标系原点。

图2 散射点模型

线阵收发分置MIMO雷达的阵列排布如图1所示，设发射阵列包含It=25个阵元，阵元间距为dt=8m，第一个发射阵元T0在真实坐标系中的坐标为(0,0,0)m，发射阵列的单位方向矢量ei=(0,1,0)；接收阵列包含Mr=25个阵元，阵元间距dr=8m，第一个接收阵R0在真实坐标系中的坐标(0,5 000,0)m，接收阵列的单位方向矢量em=(1,0,0)。采用线阵时，预设参考点O在真实坐标系中的坐标为(1 000,2 000,5 000)m。发射信号为一组正交序列调制的窄带信号，发射载频fc=10 GHz，信号带宽为0.5 MHz。线形阵列的无模糊成像范围为[-ll,ll]，ll=cR0/(2dtfc)，根据以上设置的仿真条件可知ll=20.539 6m，2ll大于目标尺寸，可以进行成像。

分别用SBL,PCSBL,IFSBL,PC-IFSBL算法对散射点模型进行成像，仿真结果如图3所示。