制导火箭末敏弹系统命中概率研究*
2019-11-13陈德明李广林
陈德明,李广林
(西安现代控制技术研究所, 西安 710065)
0 引言
命中概率研究是武器系统毁伤效能研究的基础,也是评价武器系统设计方案优劣的主要指标。文中的研究对象是携带子母式末敏战斗部的制导火箭末敏弹系统,由于其命中概率与武器系统的射击精度、目标特性、作战使用等密切相关,且在母弹飞行、战斗部开舱抛撒和末敏子弹飞行、探测、作用等工作流程实现中,所受到的影响因素极为复杂且呈随机特性,很难在有限的飞行试验中得到,因此文中采用蒙特卡洛仿真方法对制导火箭末敏弹系统的命中概率进行计算分析和研究。
传统的末敏弹命中概率为目标区内命中目标的末敏子弹数与落入目标区的末敏子弹数之比,主要考虑的是末敏子弹的工作性能。制导火箭末敏弹系统命中概率定义为对给定的目标(包括目标数量、目标大小、队形、所占区域大小等因素)进行多发重复射击,命中目标的末敏子弹数与发射的末敏子弹数之比[1]。
制导火箭末敏弹的仿真模型包括制导火箭末敏弹闭环有控弹道模型和末敏子弹减速段、扫描段、目标捕获与识别段及EFP战斗部命中目标模型等。
文中在已有制导火箭末敏弹闭环控制弹道模型基础上,建立了末敏子弹扫描运动、目标捕获与识别、EFP战斗部命中模型,选取了三种典型目标阵型,以末敏子弹对静止目标的命中概率为目标函数,运用Monte-Carlo法进行计算机仿真计算。
1 命中概率仿真模型
1.1 坐标系
为了分析方便,建立如下坐标系:
发射坐标系OXYZ:原点O为发射点,原点与目标区域中心的连线为OX轴,OY轴铅垂向上,OZ轴依右手定则确定;
扫描坐标系O1X1Y1Z1:原点O1为开始稳态扫描时,扫描中心在地面上的投影,O1Y1轴铅垂向上,O1X1轴、O1Z1轴分别与发射坐标系OX轴、OZ轴平行[2];
目标坐标系O2X2Y2Z2:原点O2为目标区域的几何中心,O2Y2轴铅垂向上,O2X2轴、O2Z2轴分别与发射坐标系OX轴、OZ轴平行。
坐标系之间的关系如图1所示。

图1 坐标关系图
1.2 弹道模型
制导火箭末敏弹母弹弹道模型和子弹弹道模型参照参考文献[3]给出,此文略。
1.3 末敏子弹稳态扫描运动模型
稳态扫描阶段,末敏子弹中的敏感器以稳定的落速和转速对目标区进行扫描。敏感轴延长线与地面的交点运动轨迹如图2所示[4]。

图2 末敏子弹稳态扫描示意图
1.4 目标捕获与识别模型
末敏子弹对目标进行探测识别时,敏感器视场扫入目标的方向是随机的,计算命中概率时,假设目标静止且长短轴在目标坐标系中的取向与O2X2、O2Z2轴一致,见图3,图中(Xmb,Zmb)为单个目标的中心坐标,a、b分别为目标在地面上投影的长和宽。A点为扫描线扫入目标的起始点,A′为扫描线离开目标的结束点,R为扫描半径,φ为矢径R与O2X2间的夹角,(Xc,Zc)为扫描中心坐标。此时目标面积Sm可表示为:
扫描线与目标交会时,如果AA′的弧长S(xA,zA)满足l≤S∈Sm时((xA,zA)为扫描线上弹轴指向点的坐标),则表示捕获到目标,可以进行目标识别。
式中l为识别准则中要求的最小尺寸。模拟仿真时,选取l=1.5 m。
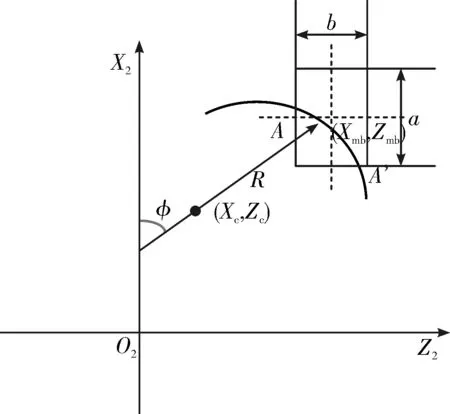
图3 目标捕获示意图
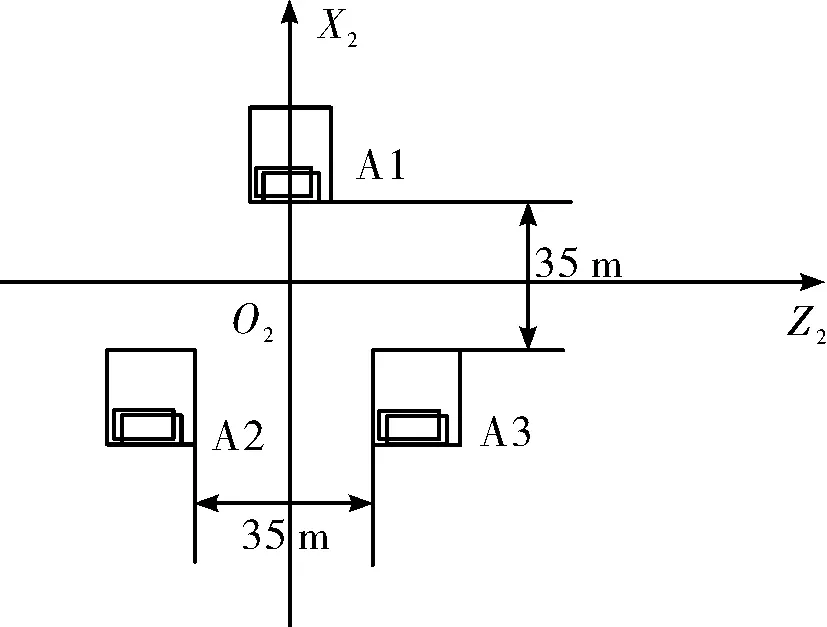
设末敏子弹的识别概率为P,则当生成的伪随机数ξ满足ξ 由于敏感器的响应波形与末敏子弹在目标上理想的扫描历程并不同步,子弹实际瞄准点时刻是在理想瞄准点时刻的基础上,向后平移了一段时间Δt,即存在识别时延。该时间可通过地面试验初步确定,而敏感轴的前置角还与末敏子弹的扫描角、扫描频率等相关,实际过程中,识别时延、扫描角、扫描频率等均为随机量,采取敏感轴前置的办法,补偿由敏感器定位精度引起的瞄准点偏差必然也是一个随机量。 式中:L为EFP射击距离。 模拟仿真时,设EFP战斗部密集度指标为0.25 m×0.25 m,并认为散布误差在距离和方向上相互独立服从正态分布规律,则每发EFP命中点的中心坐标可近似为: x=X0+1.483×Ex×ξx z=Z0+1.483×Ez×ξz 式中:X0、Z0为弧线AA′的中点坐标,ξx、ξz为符合标准正态分布N(0,1)的随机数。 a)单一目标模型 设单一目标(坦克)在地面的投影尺寸为7.5 m(长)×3.5 m(宽),目标的长边沿发射坐标系的X轴方向,目标的短边(宽)沿发射坐标系的Z轴方向,瞄准点为坦克的几何中心,其在发射坐标系中的坐标为(Xmb,Zmb),则目标4个角在发射坐标系中的坐标为(7.5/2+Xmb,-3.5/2+Zmb)、(7.5/2+Xmb,3.5/2+Zmb)、(-7.5/2+Xmb,-3.5/2+Zmb)、(-7.5/2+Xmb,3.5/2+Zmb),作为1.4节中扫描线扫入扫出计算时的比较基准。 b)实战目标队形 以某排3辆坦克为例,进攻队形如图4所示,坦克与坦克之间纵、横向间距为25~50 m,仿真计算时,取35 m。瞄准中心为目标区域中心O2点,即由坦克A1、A2、A3构成的三角形的几何中心,其在发射坐标系中的坐标为(Xmb,Zmb),单个目标尺寸:7.5 m(长)×3.5 m(宽),则可确定目标A1~A3四个角在发射坐标系中的坐标。 图4 坦克排进攻队形 以某连9辆坦克为例,进攻队形如图5所示,排与排纵向间距150~300 m,仿真计算时取200 m,排与排横向间距200~400 m,仿真计算时取300 m,瞄准中心为目标区域中心O2点,其在发射坐标系中的坐标为(Xmb,Zmb),即由排的几何中心构成连的几何中心。单个目标尺寸:7.5 m(长)×3.5 m(宽),则可确定目标A1~A9 4个角在发射坐标系中的坐标。 图5 坦克连进攻队形 c)验证飞行试验目标模型 设目标区域边界尺寸(虚框尺寸)为450 m×270 m,目标间距为纵向70 m,横向60 m,目标数量为24个,呈6行、4列排列。单个目标尺寸:7.5 m(长)×3.5 m(宽),瞄准中心为目标区域中心O2点,其在发射坐标系中的坐标为(Xmb,Zmb)。 各模拟目标点四个角相对于射击目标点的坐标如图6中标记所示。 图6 验证飞行试验模拟目标布置图 制导母弹飞行的误差源模型见参考文献[3]。 在目标捕获与识别、敏感器定位模型中,特征参数虽为随机量,但在工程实践中不可能按照随机参数设定,均按其均值设定,模拟仿真时,也按均值设定,其取值范围如1.4节、1.5节所述。 制导火箭末敏弹命中概率计算按照图7所示流程进行。 图7 命中概率计算流程图 通过建立制导火箭母弹、末敏子弹弹道模型以及末敏战斗部作用过程模型,在制导火箭末敏弹射击精度分析的基础上,建立了末敏子弹扫描运动、目标捕获与识别模型、EFP命中目标模型、模拟目标等误差模型,利用蒙特卡洛法模拟175次射击过程,逐发判断子弹是否命中目标,计算制导火箭末敏弹对特定目标的命中概率。 仿真计算结果:对前述的4种特定目标模型,在0 m及1 500 m海拔条件下进行大小射程(大射程标准射程:40 km左右,小射程标准射程:20 km左右)命中概率计算,并在计算过程中统计了EFP战斗部命中目标时的子弹高度,制导火箭末敏弹的命中概率计算结果见表1~表4。 表1 0 m海拔、大射程条件下,制导火箭末敏弹命中概率仿真结果 表2 0 m海拔、小射程条件下,制导火箭末敏弹命中概率仿真结果 表3 1 500 m海拔、大射程条件下,制导火箭末敏弹命中概率仿真结果 表4 1 500 m海拔、小射程条件下,制导火箭末敏弹命中概率仿真结果 由仿真计算结果可得出如下结论: 1)影响系统命中概率的主要因素是:系统射击精度、末敏子弹的探测识别水平和EFP战斗部的威力轴散布; 2)从仿真结果看,对于母弹的射击精度CEP不大于50 m的制导火箭末敏弹,较适合于对敌小幅员目标(坦克排)的打击作战; 3)不同海拔、不同射程条件下,命中概率变化不大,小射程条件下,母弹的闭环工作时间短,射击精度较低,导致命中概率略低; 4)从EFP战斗部作用时的高度分布情况看,大部分分布在80 m高度以上,说明在子弹扫描的初始阶段,就能够快速捕获、识别目标,母弹的制导精度保证了全弹具有较高的命中概率。 5)在确定的射击精度保证下,末敏子弹的探测识别率及EFP战斗部的威力轴散布是影响命中概率的主要因素; 6)在对连目标进行射击的过程中,命中概率较低。这是由于母弹的制导精度较高,在目前连目标分布情况下,以目标区域中心作为瞄准点时,其周围100 m之内并无目标,导致命中概率较低。武器系统实际使用时,必须考虑这些因素。 制导火箭末敏弹命中概率研究是一项非常有意义的研究内容。文中从理论分析、系统建模和仿真计算等方面较为全面地对制导火箭末敏弹在高低海拔及大小射程条件下对不同的目标对象的命中概率进行了分析计算,建立了末敏子弹稳态扫描运动模型、目标探测识别模型、敏感器定位模型、EFP战斗部命中目标模型及模拟目标模型等。仿真计算结果表明,在确定的总体参数及误差取值条件下,制导类末敏子弹药对小幅员目标的命中概率较高,为下一步进行效能分析及规范武器系统的使用,奠定了较好的基础,也为类似制导类末敏弹药命中概率的仿真研究提供了有价值的参考。1.5 敏感器定位模型
1.6 EFP命中目标模型

1.7 模拟目标模型


1.8 误差模型
2 命中概率仿真计算
2.1 命中概率计算流程
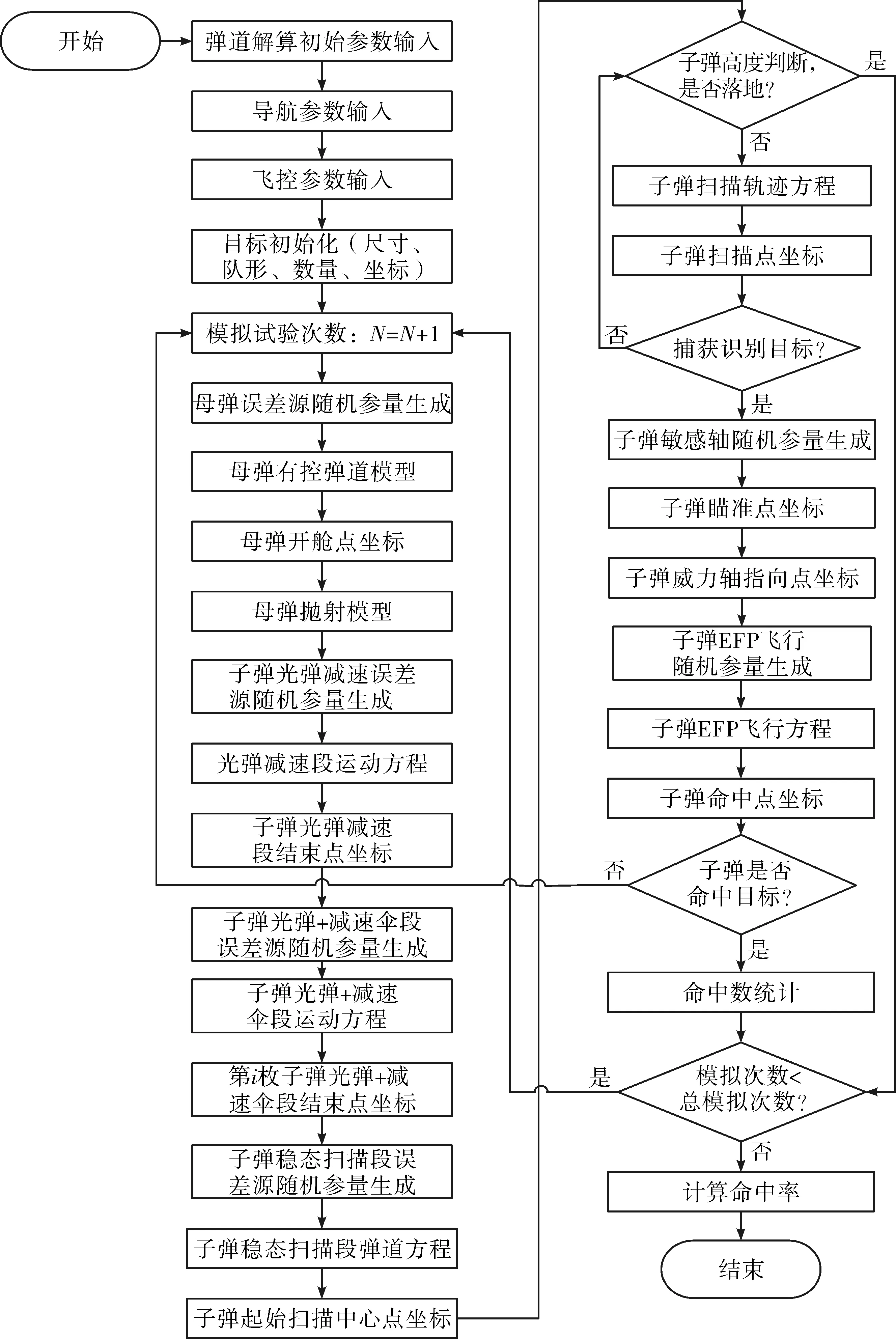
2.2 仿真计算结果




2.3 结论
3 结束语
