间断有限元求解两点边值椭圆问题的超收敛性数值研究

张作政

(长沙学院计算机工程与应用数学学院, 湖南 长沙 410022)

1973年，Reed和Hill[1]首先提出间断有限元方法求解中子输运方程.之后，用间断有限元(DG)求解椭圆方程和抛物方程几乎同时得到了快速发展.1997年，Bassi和Rebay[2]提出了一种求解可压缩Navier-Stokes方程的稳定的高阶收敛的DG格式.接着Cockburn和Shu提出了局部间断有限元(LDG)方法[3], 与此同时，Baumann和Oden[4]引入了一类新的DG方法.Arnold等人建立了基于九种不同数值通量的DG方法的统一框架[5].

连续有限元求解两点边值椭圆问题时，已经有一些超收敛结果.Douglas和 Dupont 证明了对于经典的P阶连续有限元，在网格节点处有2P阶的超收敛[6].Bakker[7-8]分别验证了在 Gauss点处数值解导数有P+1阶超收敛和数值解在 Labatto点具有P阶超收敛.陈传淼[9]对连续有限元求解两点边值椭圆问题的超收敛结果进行了详细完整的综述.

对于间断有限元求解椭圆问题，已经得到一些超收敛结果.Castillo[10]证明了一致且守恒的DG方法，数值通量在节点处是准确成立的，且在Gauss点处导数的超收敛阶为P+1.李璨[11]研究了DG方法求解一维椭圆问题的超收敛现象.后来Larson[12]又证明了，在一致网格下，使用IP-DG方法和NIPG-DG方法在节点处的数值通量均是准确的.Celiker和Cockburn[13]研究了一类DG方法求解一维对流扩散问题的超收敛性质，证明了在网格节点处守恒的数值通量和导数的通量都有超收敛性质，并且对于相应的椭圆型方程，数值通量是准确的.

本文基于局部间断有限元(LDG)方法求解两点边值问题.数值上验证了对于md-LDG方法，P+1阶的右Radau 点与左Radau 点分别是数值解U 和导数Q的P+2阶超收敛点.对于一致且守恒的间断有限元法，在数值解导数处，P阶Gauss点是P+1阶的超收敛.

1 间断有限元方法

考虑Dirichlet边界条件的一维椭圆两点边值问题

(1)

令q=u'，则方程(1)可以写成等价的一阶方程组

(2)

网格剖分为Ij=[xj-1/2,xj+1/2],j=1,2,...,N.

其中x1/2=0,xN+1/2=1.离散区间的中点为xj=(xj-1/2,xj+1/2)/2，单元长度hj=|Ij|，最大步长

用试验函数v和w分别去乘(2)的前两个方程，并在每个单元Ij上分部积分得到

(3)

下面定义DG方法的弱形式.为此先定义间断有限元空间Vh为

Vh={v:v∈PP(Ij),j=1,2,3,...,N},

其中PP(Ij)表示Ij上次数不超过P次的多项式集合.则弱形式为求U,Q∈Vh， 使得对任意v,w∈Vh，在每个单元Ij上满足

(4)

表1和表2列举了一些经典DG方法的数值通量取法，表2中的罚参数α在边界取为

α(0)=α(1)=p/h.

表1 内部节点的数值通量

表2 边界处导数的数值通量

2 数值实验

本节主要是用数值实验验证间断有限元求解两点边值椭圆问题的超收敛性.为简单起见，在所有的数值实验中，在模型(1)中取f=(2π)2cos(2πx).其中u0=u1=1，准确解u(x)=cos(2πx).

本节中所有超收敛结果对均匀和非均匀网格均成立.非均匀网格按下列方式产生.hi,j代表第i层网格第j个单元长度.ni为第i层网格单元个数.第1层网格单元数n1=4.h1,1=0.4,h1,2=0.1,h1,3=0.1,h1,4=0.4.

从第2层网格开始，按照如下规则产生：

其中ni=2ni-1.非均匀网格的第1到第5层网格单元分布图见图2.1.所有表格中的第1列p代表逼近多项式的阶数.第2列表示网格的单元数，N=3,4,...,7代表有

2N个单元数.相关范数定义为

图2-图9展式了数值解U和导数Q的误差曲线图.图2，4，6，8中每个单元里的*代表右Radau多项式的零点，图.3，5，7，9中每个单元里的*代表左Radau多项式的零点.从图2-9可以显然的看到右Radau多项式的零点非常靠近U的误差曲线的零点，而左Radau多项式的零点非常靠Q的误差曲线的零点.从而数值上证实了右Radau点是u的超收敛点，而左Radau点是q的超收敛点.

为了进一步证实md-LDG在Radau点的超收敛性质，表3和表4分别列举了在均匀网格和非均匀网格下数值解U和导数Q的L2和L误差收敛阶.从表3-4和图10-13中可以看到在右Radau点和左Radau点都有P+2阶的超收敛，相应的L2误差只有P+1阶的丰满阶.

对于一致且守恒的间断有限元具有类似的超收敛结果，本文只列举了LDG II 方法相应的超收敛数值结果.图14-15分别画出了LDG II 方法在p=1和p=2时数值解导数Q的误差曲线图.图14-15中的*代表每个单元的Gauss点.从图14-15中可以观察到每个单元的Gauss点非常靠近Q的误差曲线的零点.与表1和表2相似，表5-6列举LDG II方法类似的数值计算结果，但其中||u-U||和||q-Q||表示为每个单元上的Gauss点误差的L范数.从表5-6中可以看到在Gauss点的L范数对U和Q都是p+1阶，而相应的L2范数对U是p+1阶，对Q是p阶，故对于LDG II方法每个单元Gauss点处，不是数值解U的超收敛点而是数值解导数Q的超收敛点.

表3 均匀网格下的md-LDG的收敛阶

表4 非均匀网格下的md-LDG的收敛阶

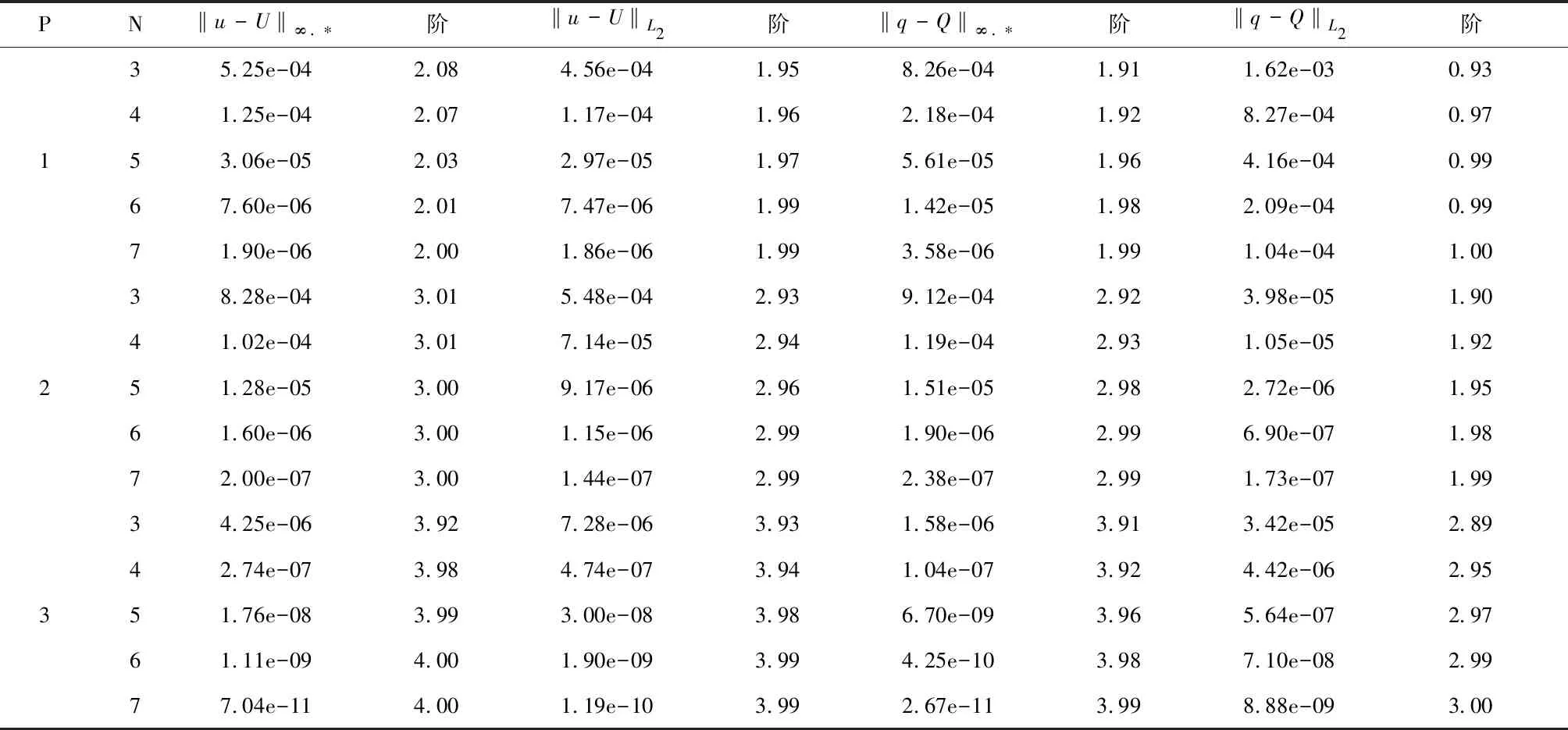
表5 均匀网格下的LDG II的收敛阶

表6 非均匀网格下的LDG II的收敛阶

图1 非均匀网格

图2 md-LDG均匀网格下U的误差曲线，p=1

图3 md-LDG均匀网格下Q的误差曲线，p=1

图4 md-LDG均匀网格下U的误差曲线，p=2

图5 md-LDG均匀网格下Q的误差曲线，p=2

图6 md-LDG均匀网格下U的误差曲线，p=3

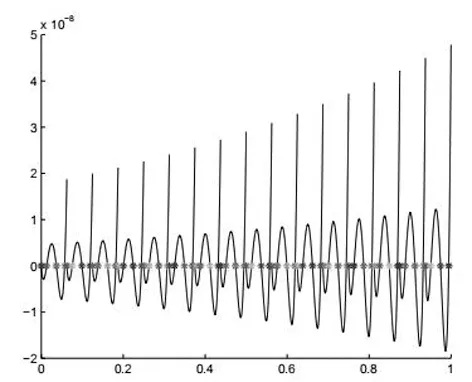
图7 md-LDG均匀网格下Q的误差曲线，p=3

图8 md-LDG均匀网格下在右Radau点的U的误差收敛曲线，

图9 md-LDG非均匀网格下在右Radau点的U的误差收敛曲线，

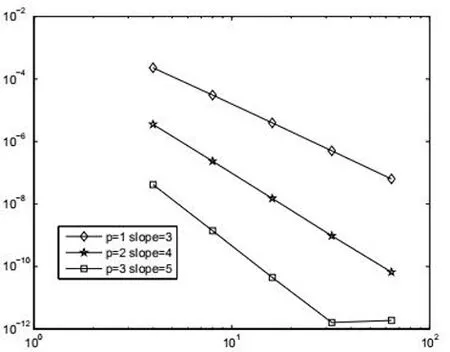
图10 md-LDG均匀网格下在左Radau点的Q的误差收敛曲线

图11 md-LDG非均匀网格下在左Radau点的Q的误差收敛曲线

图12 LDG II均匀网格下Q的误差曲线， p=1

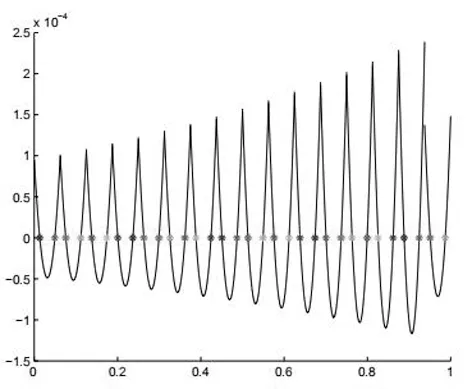
图13 LDG II均匀网格下Q的误差曲线，p=2

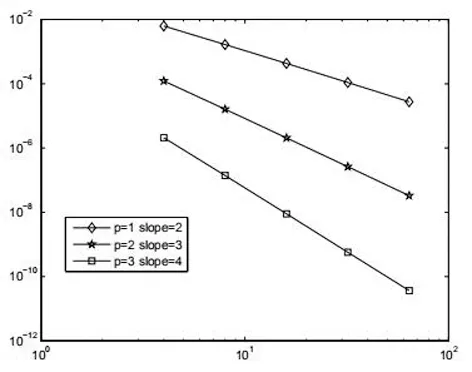
图14 LDG II均匀网格下在Gauss点的Q的误差收敛曲线

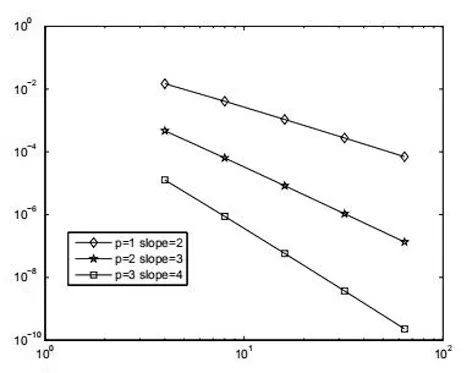
图15 LDG II 非均匀网格下在Gauss点的Q的误差收敛曲线

3 结语

本文从数值上研究了间断有限元方法求解一维椭圆问题的超收敛性质.对于md-LDG方法，P+1阶的右Radau 点与左Radau 点分别是数值解U 和导数Q的P+2阶超收敛点.对于其他一致且守恒的间断有限元法，对于数值解导数Q，P阶Gauss点是P+1阶的超收敛.从数值实验的结果来看，md-LDG方法相比其他的一致且守恒的间断有限元方法具有更多的超收敛性质.不同的DG方法不仅可能具有不同的超收敛阶，而且可能具有不同类型的超收敛点.高维问题的间断有限元的超收敛性质将是下一步研究的方向，另一方面，我们将研究奇异摄动微分方程的超收敛性质.