超高维判别分析中的迭代稳健特征筛选方法
2019-11-11何胜美
何胜美
(广东金融学院 金融数学与统计学院,广东广州510521)
随着科学技术的发展,大数据成了当下研究的热点.高维作为大数据的主要特征,得到了学者们的广泛关注.在数据分析中,当特征的维数超过样本量,统计建模分析将面临巨大的挑战.对于高维数据,涌现出来一批倾向于精确变量选择的方法,例如 LASSO[1],SCAD[2],Elastic net[3]以及它们的各种扩展[4-5].但是,超高维时,上述变量选择方法在计算成本,统计的准确性以及算法的稳定性上都遇到巨大挑战.Fan和Lv在线性模型假情况下,利用边际皮尔森相关性对协变量做初步筛选,提出了确定性独立筛选方法(SIS),证明在一定条件下该方法满足确定筛选性质,即模型所选变量集合包含全部真实变量的概率趋近于1,首次提出了变量筛选的概念[6].随之而来,各种以边际效用为基础的变量筛选方法相继涌现.比如线性与广义线性模型上有基于最大边际似然的筛选方法[7]和基于边际经验似然比的变量筛选方法[8].非参数方法上有Fan等的基于b样条估计边际相关效用的非参数独立筛选[9]、NIS,Li等的基于Kendall相关的变量筛选方法[10]、距离相关筛选方法[11]、球相关变量筛选方法[12]等.针对超高维判别分类问题,也有相关变量筛选方法出现,例如Ma 和 Zou 的 Kolmogorov filter(KF)[13];Cui等的适用于多分类的稳健特征筛选方法 MV-SIS[14]及其修正方法 AD-SIS[15].
边际思想让变量筛选方法能够对超高维模型进行快速降维,但是它忽略了变量间可能存在的强相关性,进而导致漏选重要变量或者错选不重要的变量.为解决这个问题,很多方法都提出了相应的迭代筛选形式,例如 ISIS[6],ISIRS[16],DC-ISIS[17],MBKR-ISIS[18]和 QC-ISIS[19],但上述这些方法主要针对连续变量问题,对于超高维分类问题的变量筛选,相应的迭代筛选还没有得到充分的研究.
本文在Cui等人提出的MV-SIS[14]和He等人提出的AD-SIS[15]的研究基础上,考虑超高维分类数据的判别分析的迭代变量筛选问题.结合Zhu等的思想[16],提出了超高维判别分类问题中的迭代特征筛选方法MV-ISIS和AD-ISIS,并通过数值模拟,研究了这两种方法的有限样本效果.
1 迭代特征筛选方法
1.1 MV-SIS和AD-SIS
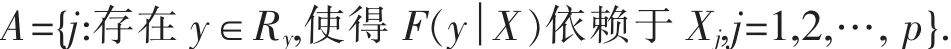
这里 F(y│X),是给定 X 的条件下 Y 的分布函数.则若 j∈A,Xj为重要变量,反之,若 j∉A,Xj为不重要变量.令F(x)=Pr(X≤x)是随机变量X的分布函数,Fr(x)=Pr(X≤x|Y=yr)是给定Y=yr的条件下,X的条件分布函数,以及pr=P(Y=yr),Cui等人提出了:

来刻画X与Y的依赖性[14].显然,MV(X│Y)=0当且仅当X与Y相互独立.因此MV(X│Y)可以作为变量筛选指标.给定n个独立同分布的样本{(Xi,Yi),i=1,2,…,n},Cui等提出了适用于超高维判别分析的变量筛选方法 MV-SIS[14]来求如下特征集合:

其中,d=[n/log(n)],ωˆk是第 k个变量相应指标的样本估计,其具体计算如下:
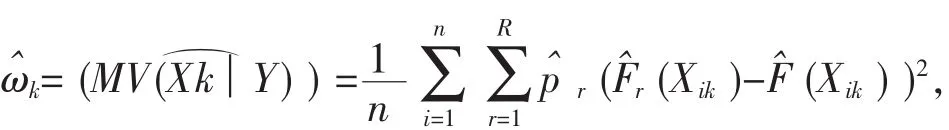
对于厚尾数据,MV-SIS并不能很好反映条件分布函数与无条件分布函数在尾部的差异,He等通过引进权重函数φ(F(x))=1/F(x)(1-F(x))对MV-SIS进行修正,得到:
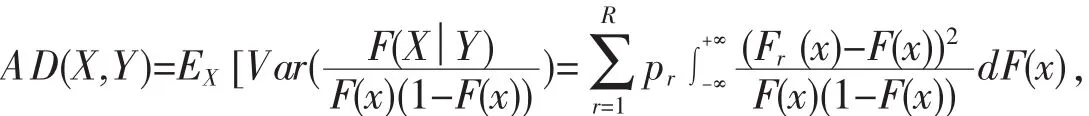
以及:

以此得到新的适用于判别分析的超高维特征筛选方法AD-SIS[15].
1.2 迭代特征筛选MV-ISIS和AD-ISIS
MV-SIS和AD-SIS在数值模拟研究和实际数据研究中都显示了不错效果.但是,二者都是基于某一边际效应指标的特征筛选方法,忽略了变量间可能存在的强相关性,进而可能导致漏选重要变量或者错选不重要的变量.类似于Zhu等的思想[16],本文基于MV-SIS(AD-SIS)做如下迭代算法:
第一步,应用变量筛选方法MV-SIS(或者AD-SIS)对观测样本(X,Y)进行筛选,记这一步中筛选的变量.
第二步,记 X1=(X1A1,X2A1,…,XnA1),显然,X1是是 n×(p-|A1|)矩阵.然后,进一步利用 MV-SIS(或者 AD-SIS)对新数据(Xnew,Y)进行变量筛选,筛选出另外d2个特征,记为
第三步,更新A1=A1∪A2和d1=d1+d2,再重复第二步,直到筛选的变量达到预先给定的数量.最终筛选的变量集合设为A1,则变量数量为d=|A1|.
上述迭代筛选方法简记为MV-ISIS和AD-ISIS.其中,通常设定d=[n/log(n)],实际模拟中选择d1=d2=5.另外,注意到与 Xnew不相关,因此,MV-ISIS(或者AD-ISIS)能在一定程度上解决变量间可能存在的强相关导致的漏选重要变量或者错选不重要的变量的问题.
2 数值模拟
下面通过蒙特卡罗模拟来评价迭代筛选算法MV-ISIS和AD-ISIS的效果.
例1 考虑其中,预测变量生成于正态分布 N(0p,Σ)的随机向量,0p是 p 维零向量,Σ=(σij)p×p为协方差矩阵,满足:(1)σij=1,i=1,2,…,i≠4;(3)σij=ρ,i≠j,j≠4 和 i≠4.ε 为误差项.按照下列规则离散化得到 Y:
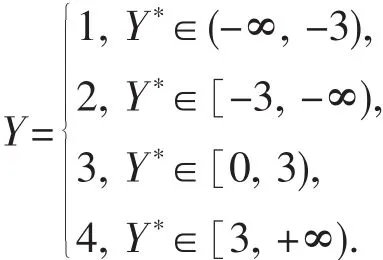
显然,该模型中,Y依赖于X1,X2,X3和X4,但是不难计算Cov(Y*,X4)=Cov(5X1+5X2+5X3-155Cov(X1,X4)+5Cov(X2,X4)+5Cov(X3,X4)-15=0.因此,Y*与X4是边际独立的,从而 Y 与 X4也是边际独立的.取 n=200,p=2 000,考虑以下情况:(1)ρ=0.5 和 0.8;(2)ε~N(0,1)和 ε~t(1).
分别利用MV-SIS,AD-SIS,MV-ISIS和AD-ISIS对生成的数据进行变量筛选,比较它们变量筛选的效果.通过500次独立重复模拟,统计变量Xi正确筛选的频率pi,i=1,2,3,4,同时4个变量同时正确筛选的频率pa,结果如表1和表2所示.

表1 例1中误差项 ε~N(0,1)情形下模拟数据变量筛选结果

表2 例1中误差项ε~t(1)情形下模拟数据变量筛选结果
表1和表2结果表明,MV-SIS和AD-SIS的变量筛选结果受到变量间的相关性影响较大,当变量间相关系数由0.5增长到0.8时,变量X1,X2和X3被正确筛选的频率有较大的下滑(无论误差项是标准正态情形还是t(1)分布情形).而迭代筛选算法有效的解决了上述问题,尤其是对于p=0.8高相关的情况,MV-ISIS(AD-ISIS)大幅度提高了变量X1、X2和X3被正确筛选的频率.例如在表2中,当p=0.8时,MV-SIS和ADSIS对第一个变量筛选的概率p1只有0.690和0.712,但迭代方法的结果有了较大提升,MV-ISIS和AD-ISIS均为为0.998,其它情况也都有类似的结果.而对于X4的筛选,由于X4与类别变量Y边际独立,MV-SIS和AD-SIS在各种情况下都未能正确的将X4筛选出来,相应的概率p4都为零,从而导致4个变量全部被正确筛选的概率pa全为零.而两种迭代筛选方法得到了满意的结果.表2结果显示,在误差项,ε~t(1),p=0.8时,MV-ISIS和AD-ISIS对应的p4分别从零上升到了0.864和0.918,相应的pa也从零分别提高到了0.864和0.918.
3 结语
本文研究了超高维判别分类问题中的迭代变量筛选问题,针对以往边际筛选方法忽略了变量间可能存在的强相关性,进而可能导致漏选重要变量或者错选不重要的变量的问题,提出了两种迭代稳健变量筛选方法MV-ISIS和AD-ISIS,并通过数值模拟,讨论了这两种方法在有限样本上的效果.模拟结果表明,在判别分类模型中,某些不重要变量与重要变量高度相关,而其他重要变量与类别变量的相关性较弱;或者某些变量与类别变量边际相关性较弱,但联合相关性又较强时,MV-ISIS(或者AD-ISIS)能大幅提高原始方法MV-SIS(AD-SIS)的变量筛选效果.
