复合型Laguerre方程边值问题解的相似结构

李顺初，张红丽*，郑鹏社，桂钦民

（1.西华大学 应用数学研究所，四川 成都610039；2.北京东润科石油技术股份有限公司，北京100029）

在处理石油等领域实际问题时，经常会涉及微分方程，所以研究方程解的内在规律是简化求解方程不容忽视的一步，方程的解式能否用统一的式子来表示呢？近年来，就有相关研究报告给出了肯定的回答，并且逐步构成了微分方程解的相似结构理论［1-6］.

Laguerre方程在统计学［7-9］、量子力学［10-11］领域有着广泛的应用，但在以往的研究中，却没有针对复合型Laguerre方程解的相似构造进行研究.鉴于以上研究的思路，本文研究了复合型Laguerre方程［12］边值问题：

其中：D、E、F、K、H、a、b、c、n、α、β 为已知实常数，且 D≠0，K2+H2≠0，0＜a＜b，n 为正整数.

1 预备知识

引理1［12］Laguerre方程的通解可以写为：

其中，A1、A2、B1、B2为任意常数是 Laguerre 多项式，Gi(-ni,1,x)是第二类 Kummer函数.

引理2［12］已知 F(α,γ,x)为第一类 Kummer函数，则

依据引理 2，以及 Lni(x)与 F(-ni,1,x)的关系：Lni(x)=ni！F(-ni,1,x)；Gi(-ni,1,x)与 F(-ni,1,x)的关系：Gi(-ni,1,x)=F(-ni,1,x)lnx-1.求得：

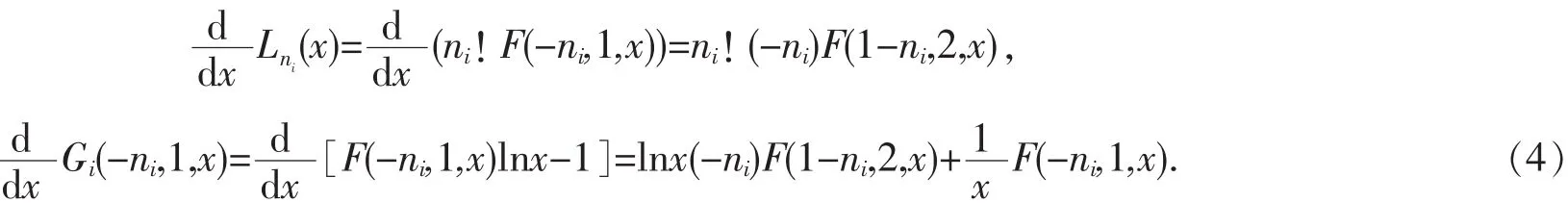
引理3 对于二元函数：

有：

其中：i=1 代表左区(a＜x＜c)，i=2 代表右区(c＜x＜b).

2 解的相似结构

本文的证明思想是，首先论证下面的相似结构定理.

定理 1若边值问题（1）有解，则它的左区(a＜x＜c)解为：

右区(c＜x＜b)解为：

其中：ψ*(x)称为右（区）相似核函数：

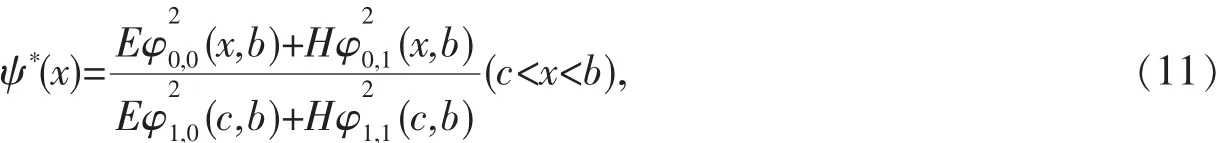
ψ(x)称为左（区）相似核函数：

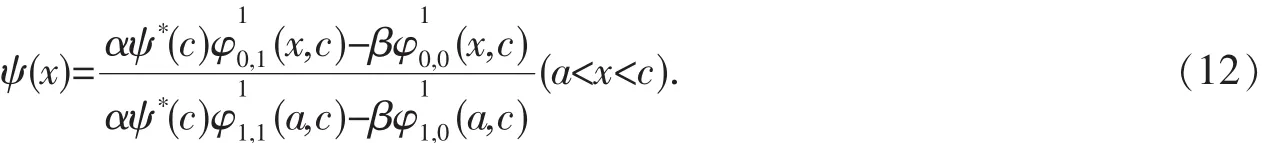
证边值问题（1）的定解方程是 Laguerre方程，根据引理1，可以得到(1)的通解为：

其中 A1、A2、B1、B2为待定常数，可以由边值问题(1)左右边界条件确定待定常数 A1、A2、B1、B2.

由边值问题(1)的左边界条件B1知：

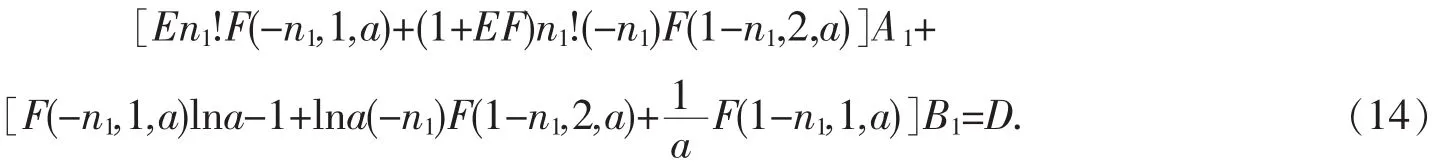
由边值问题（1）的右边值条件［Ky2+Hy2′］x=b=0知：

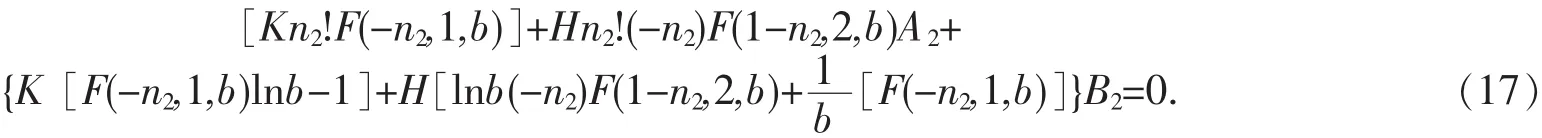
根据边值问题（1）有唯一解［13］可以得到，关于待定系数 A1、A2、B1、B2的线性方程组（14）～（17）的系数行列式△≠0，且经过计算得：

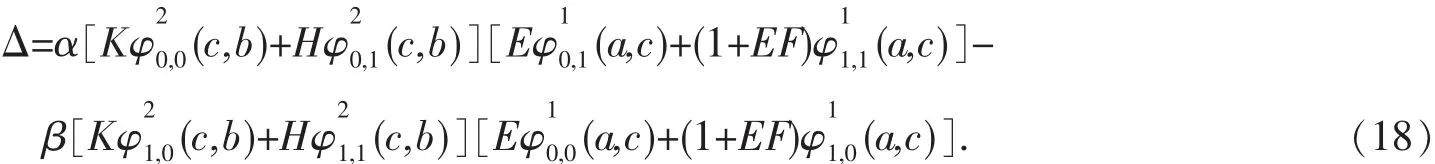
求解线性方程组（14）～（17），得：

推论1在边值问题（1）中，如果右边界条件为y2(b)=0(即K≠0,H=0),则其对应的右相似核函数为：

推论2在边值问题（1）中，如果右边界条件为y2′(b)=0(即K=0,H≠0)，则其对应的右相似核函数为：

推论3 边值问题（1）的解式与它的导数存在有如下性质：

3 相似构造法步骤

第一步：构造引解函数.

利用边值问题（1）的左右区定解方程的两个线性无关的解Lni(x)与Gi(-n,1,x)(i=1,2)，作出引解函数：

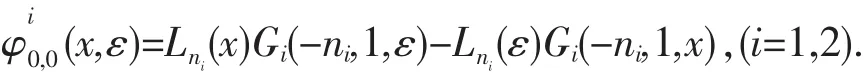
第二步：构造左右相似核函数.

第三步：获得边值问题的解.

对复合型 Laguerre 方程边值问题（1），根据（9）式，结合左边界条件［Ey1+(1+EF)y1′］x=a=D 的系数 E、F、D和左相似核函数ψ(x)，组合整理即可得到该边值问题的左区间解；同理，根据（10）式，通过对［Ey1+(1+EF)y1′］x=a=D 的系数 E、F、D，左引解函数、交界面条件系数α、β与右相似核函数ψ*(x)进行组合整理，即得到该边值问题的右区间解.

实例求解如下边值问题：

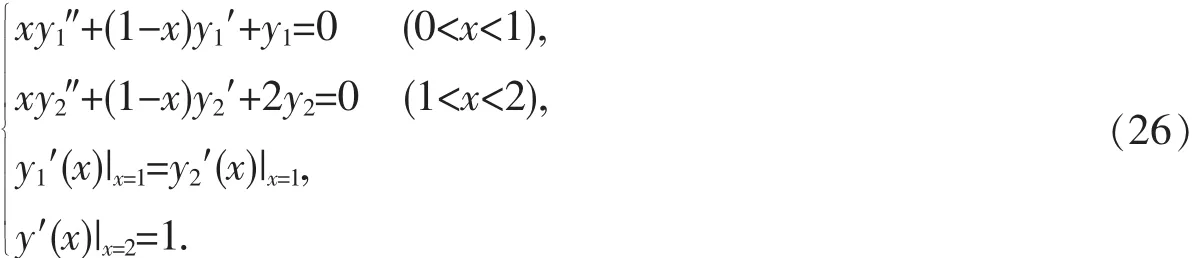
与边值问题（1）对比可知，在本例中，a=0,c=α=β=1,b=2,n1=1,n2=2,E=0,K=0,F=H=D=1.根据相似构造法的步骤，可直接求解出边值问题（26）的解.

第一步：构造引解函数.

根据方程 xy1″+(1-x)y1′+y1=0(0＜x＜1)的两个线性无关的解，构造引解函数(x,ε)=L1(x)G1(-1,1,ε)-L1(ε)G1(-1,1,x).

同理，根据方程 xy2″+(1-x)y2′+2y2=0(1＜x＜2)的两个线性无关的解，构造引解函数(x,ε)=L2(x)G2(-2,1,ε)-L2(ε)G2(-2,1,x).为方便，记 Gi(x)=Gi(-ni,1,x).

第二步：构造左右相似核函数.

根据（11）式，获得右相似核函数如下：

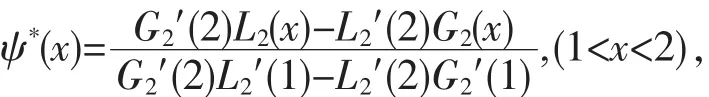
并求得：

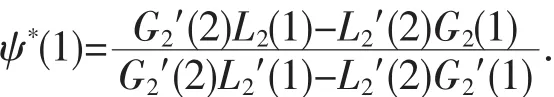
同理，根据（12）式，获得左相似核函数如下：

并求得：

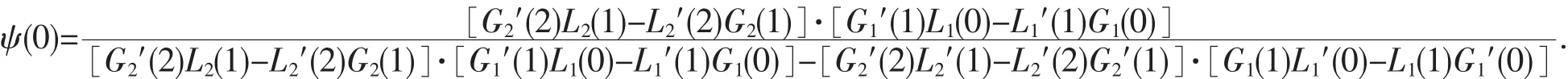
第三步：获得边值问题的解.

根据（9）式即可得到边值问题（1）的左区间解：

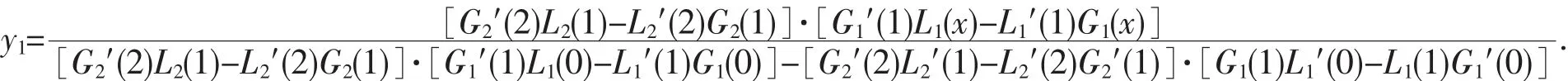
根据（10）式即得到边值问题（1）的右区间解：

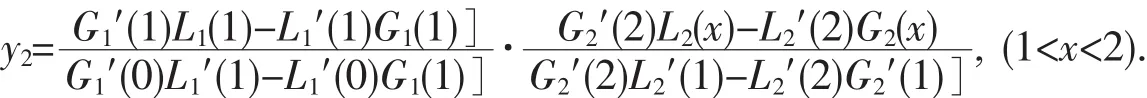
其中：

4 结论

复合型Laguerre方程边值问题的左区间解(9)式，可由左边界条件的系数E、F、D和左相似核函数(0)进行组装，且能用统一的式子表示；右区间解（10）式，可由交界面条件的系数α、β和右相似核函数ψ*（x）进行组装构成.

左相似核函数ψ(x)与右相似核函数ψ*(x)是由右边界条件系数K、H交界面条件的系数α、β和Laguerre方程的两个线性无关Lni(x)、Gi(-n,1,x)来构成.

随着右边界条件，交界面条件的系数的改变而改变相应的左、右相似核函数［14-16］，可以得到Laguerre方程的边值问题的解的相似结构式从而避开复杂的运算，提高求解的效率.