基于大数据分析的死缓限制减刑司法适用研究

陈 敏，李书琪，广文革

（1．西安理工大学 人外学院，陕西 西安710054；2．北京交通大学 理学院，北京100044；3．陕西省高级人民法院，陕西 西安710063）

一、引 言

中国《刑法修正案（八）》创制了死缓限制减刑制度，八年来，司法实践中判处死缓限制减刑的判决日益增多，该制度的研究也在饱受争议中不断成长，历史的车轮推动着此制度的研究从初始的实质法解释学研究，进入今天制度后时代的法教义学研究。理论界围绕死缓限制减刑的性质、宣告时间、裁判标准、量刑情节的适用等问题展开了较为热烈的讨论，其在饱受争议中不断前行并日渐丰富。《刑法修正案（八）》规定了死缓限制减刑的条件，但立法规定较为笼统，至今也没有相关司法解释对此制度进行细化。2011年最高人民法院《关于死刑缓期执行限制减刑案件审理程序若干问题的规定》也仅涉及死缓限制减刑的程序问题，使得法官对死缓限制减刑司法适用的把握难上加难，各种因素的叠加使法官对此制度的尺度把握不一，结果造成死缓限制减刑适用的异化［1］。由于死缓限制减刑司法适用标准尚未确定，各地法院未做到严格统一执行该项制度，此制度存在着自我失灵的天然缺陷。法官必须理性行使自由裁量权，也就是要高度重视死缓限制减刑的量刑规范化工作。法官对涉及死刑的案件是否决定适用死缓限制减刑，必须对各种情节或因素进行权衡，进行司法裁量上的价值判断［2］。法定情节和酌定情节、从宽情节和从严情节到底在裁判中占多大的分量？如将此纳入量刑规范化、科学化的考察，就可避免法官肆意行使自由裁量权导致死缓限制减刑司法适用的异化［3］。

关于死缓限制减刑制度的法律性质，是一个根本性的问题，是此制度适用的前提和基础。目前理论界与实务界对死缓限制减刑制度的性质产生重大分歧，主要包括两种观点：死刑中间说和死缓法律后果说。按照最高法院司法解释，死缓限制减刑制度的法律性质明确为死刑中间说，全国人大法工委也支持该学说。死刑中间说的学者认为，死缓限制减刑同死刑立即执行和死刑缓期两年执行（以下简称“死缓”）都是死刑的执行方式，因此在死刑裁量时法官根据犯罪情节等情况有三种选择，这在理论上是可以成立的［4］。然而，最关键的问题是法官们如何根据犯罪情节等情况对死刑的三种执行方式进行准确科学的界分，从而准确的适用死刑。三者之间的区分模糊不清，导致法官在死刑裁量时没有可供参照的标准，从而导致死缓限制减刑在司法适用中的异化。面对以上问题，死刑中间说的学者也是一筹莫展，如黎宏教授虽然坚持死刑中间说，并未提出如何科学界分死刑三种执行方式的明确标准。还有一些学者通过列举的方式提出死缓限制减刑适用更为详尽、具体的案件情节，然而仍存在能否解决司法适用疑难的问题。同时，这些学者的观点，只是就单一情节下如何适用死缓限制减刑表达自己的看法，并未涉及多重情节，特别是多种双重情节逆向竞合情况下，死缓限制减刑如何适用的问题。而上述情形是司法实务中的常态。相反，只具有单一情节的案件是例外。因此，截至目前，不论哪种学说都未从理论上提出有效解决死缓限制减刑司法适用难题的学术方案。

本文打破以往针对死缓限制减刑单纯从法学解释或者社科法学进行研究的桎梏，试图运用比较研究法梳理出此制度司法适用后时代时期凸显的问题和矛盾所在，从多学科视角探索出logistic模型来切实可行的解决死缓限制减刑司法适用的学术路径。中国在运用logistic模型解决法律适用中疑难问题的研究比较晚，针对死缓限制减刑的司法适用研究更是一片学术洼地。这种研究一般就是司法实践中评估经验的汇集，缺乏更深层次的分析。本文创新之处就是采用SPSS统计分析软件进行了体系化的模型构建，以此来估计犯罪人的主观恶性和人身危险性，将学理探究建立在大数据统计、案例分析、统计学分析的路径之上，从而实现死缓限制减刑精准的司法适用。

本文通过中国裁判文书网公布的案例随机遴选实证研究样本，分别输入关键词“死刑立即执行”、“死缓限制减刑”、“死缓”检索生效判决，随机抽取判处死刑三种执行方式的生效判决共1 300份。从收集的样本案例可看出，死缓限制减刑情节适用不统一、裁判思路不一致并非个别现象，反映了该问题的严重性。从作出判决的法院来看，不但遴选样本所涉及的中级人民法院存在上述问题，很多地方高级人民法院也存在上述问题；从省份分布看，多个省份都有类似问题出现。因此，“量刑情节适用模糊、裁判逻辑思路混乱”等现象是从不同侧面交叉反应了死缓限制减刑司法适用的问题，这些问题具有一定的代表性和可研性。目前中国司法实践中考虑的量刑情节多达30多种，其中，既有从宽情节又有从严情节，既有法定量刑情节又有酌定量刑情节。由于死缓限制减刑适用缺乏明确的标准，使得裁判者没有清晰的思路可供借鉴，由此也导致量刑情节适用的混乱［5］。因此，本文试图通过对上述司法判决梳理统计以及模型的数据分析，构建死刑司法判决辅助化量刑系统，从而实现死刑量刑的规范化、科学化。

二、Logistic模型

线性回归模型是统计学中非常广泛使用的分析数据方法，用线性关系来表达随着自变量的变化因变量是如何变化的。但考虑到量刑时响应变量是一个分类变量（“死刑”“死缓限制减刑”“死缓”），而不是一个连续变量，所以对于这种问题需要使用非线性函数构建模型［6］。在二分类因变量分析中，经常使用的累积分布函数有Logistic分布，标准正态分布（Probit模型），t分布等等，其中，在社会科学问题的分析中使用最广泛的是Logistic分布［7］。

假设观测到n个独立的二分类因变量（y1，y2，…，yn），其中yi是服从于参数为pi的伯努利分布，pi与一系列的解释变量（离散或者连续）有关。引入潜在变量（z1，z2，…，zn），假设zi与自变量之间存在一种线性关系，即zi＝xTiβ＋εi。定义当zi＞0时，令yi＝1，反之，zi＜0时，令yi＝0。则：

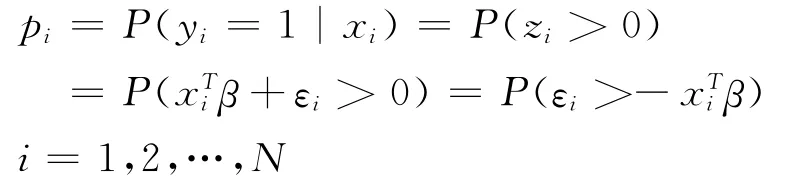
其中β是一个k×1的未知的参数向量，xTi＝（xi1，xi2，…，xik）为已知的解释变量。

本文定义εi服从均值为0，方差为π2／3的标准Logistic分布，由于Logistic分布是对称的［8］，那么

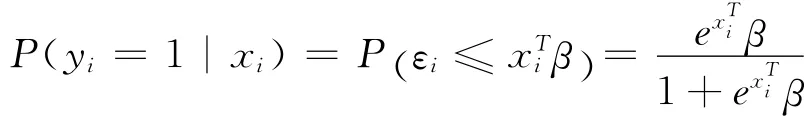
Logistic分布函数的累计概率曲线如图1所示。观察图像可知，无论xTiβ取何值，P（yi＝1｜xi）的取值范围始终在0～1之间。上述非线性函数可以使用Logit变换转变为线性函数。

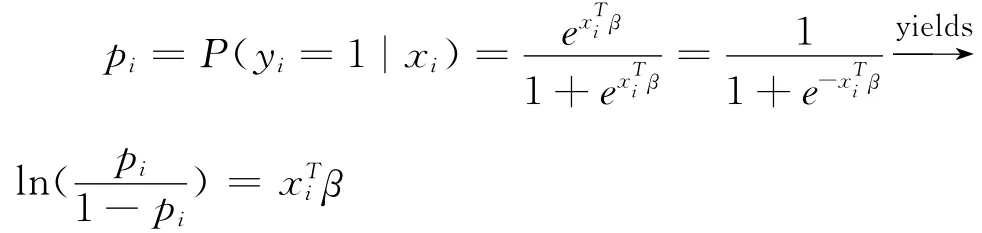
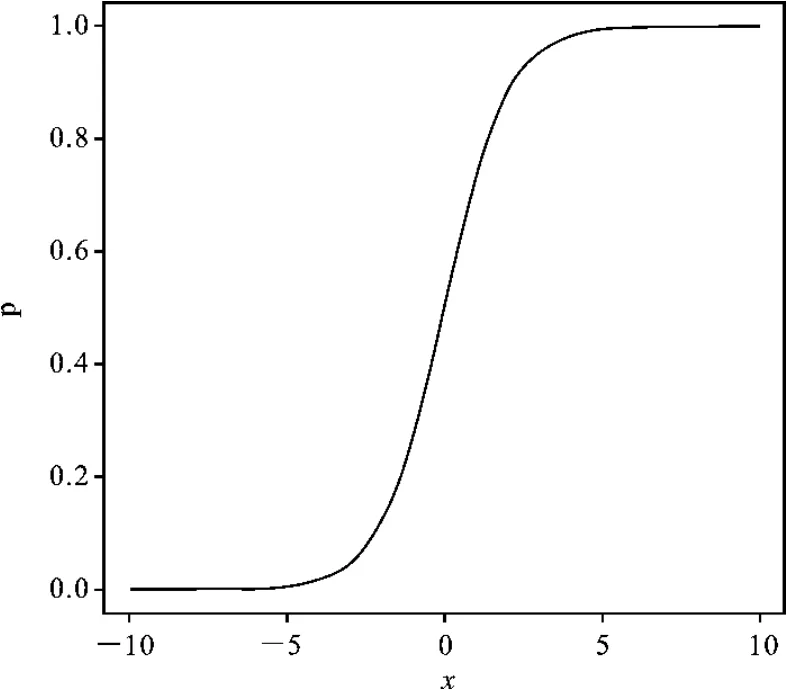
图1 Logistic分布的累积概率曲线图

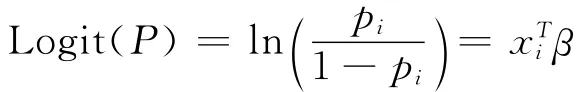
Logistic分布函数还有一个特性，那就是在xTiβ取值在0附近时，事件发生的概率随着解释变量的改变变化幅度很大，但是解释变量的值趋于两端时，事件发生的概率不会变化太大［9］。以本文的背景来说，当罪犯的罪行严重程度增加时，判死刑的概率越来越大，在中间状态时，可能很小的因素都会影响判决结果。但到罪行严重到一定程度时，再有影响判决的因素，判死刑概率的变化就没那么大了，因为还要考虑到极端事件的存在［10］。因此，Logistic回归模型很贴合我们所要讨论的量刑问题，下面我们建立量刑指标体系。

三、数据来源与指标体系

1．量刑指标体系

死缓限制减刑司法适用的实质条件，《刑法修正案（八）》和《关于死刑缓期执行限制减刑案件审理程序若干问题的规定》中都可找到相关规定。上述条文中关于死缓限制减刑司法适用的实质条件分别表述为：“根据犯罪情节等情况”和“根据犯罪情节、人身危险性等情况”，显然这样的条文规定过于模糊笼统，为司法适用的混乱留下空间。本文认为可以从主观和客观两个方面把握死缓限制减刑的实质条件，主观方面包括犯罪分子的年龄、犯罪动机、犯罪后的认罪、悔罪态度还有以往表现等，客观方面包括犯罪分子所犯罪行的性质、犯罪手段、情节是否恶劣、造成的实际危害后果，将上述死缓限制减刑司法适用问题抽象为统计学定性变量的预测问题，最终筛选出立功及重大立功、自首、未遂、坦白等21个对于判决结果具有重要意义的法定量刑情节作为解释变量，并对样本添加标签，见表1。

表1 解释变量及其标签表

2．数据来源及使用软件

本研究数据来源为中国裁判文书网，实际整理案例为1 300例，经过数据预处理，即进行缺失值替换、异常值检测与剔除，最终得到有效案例共900例，其中包括死刑立即执行300例、死缓限制减刑300例、死刑缓期执行300例。本文使用软件SPSS 25对数据进行拟合与计算。

四、模型拟合与分析

1．量刑判决概率的测算及评价

考虑到本文所选择的每个解释变量都有其实际背景意义且对最终结果都有较大的影响，所以本文不做变量选择，将所有解释变量均纳入模型。

本文将建立一个两阶段的概率测算模型，先将死缓限制减刑和死缓纳为一类均标记为0，将死刑标记为1，建立模型一。再从从缓刑样本中，将死缓标记为0，死缓限制减刑标记为1，建立模型二。

在线性回归中，主要采用最小二乘法（LSE）进行参数估计。与LSE相比，极大似然估计法（MLE）可以用于更为复杂的非线性估计。它是利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。故本文使用极大似然方法进行参数估计［11］。

第一，模型一的建立及检验（死刑或缓刑）。模型一的极大似然估计的结果如表2所示。

表2 模型一参数估计和显著性检验结果表

模型预测的结果是得到每一个样本的响应变量取1的概率，为了得到分类结果，需要设定一个阈值p0，当p大于p0时，认为该样本的响应变量为1，否则为0。阈值大小对模型的预测效果有较大影响。

通常选择接受者操作特性曲线（Receiver operating characteristic curve，简称 ROC曲线）作为评价Logistic回归模型的指标［12］。在计算ROC曲线的过程中，设置了两个指标：

TPR（正确覆盖率，True Positive Rate）：将实际的1正确地预测为1的概率。

FPR（错误覆盖率，False Positive Rate）：将实际的0错误地预测为1的概率。

TPR与FPR相互影响，而我们希望建立的模型能够使TPR尽量地大，而FPR尽量小。影响TPR与FPR的重要因素就是上文提到的“阈值”。当阈值为0时，所有的样本都被预测为正例，因此TPR＝1，而FPR＝1。此时的FPR过大，无法实现分类的效果。随着阈值逐渐增大，被预测为正例的样本数逐渐减少，TPR和FPR各自减小，当阈值增大至1时，没有样本被预测为正例，此时TPR＝0，FPR＝0。

由上述变化可以看出，TPR与TFR存在同方向变化的关系（这种关系一般是非线性的），即为了提升TPR（通过降低阈值），意味着FPR也将得到提升，两者之间存在相互制约的关系。本文希望能够在牺牲较少的FPR的基础上尽可能地提高TPR，由此画出了ROC曲线。当预测效果较好时，ROC曲线凸向左上角的顶点。平移图中对角线，与ROC曲线相切，可以得到TPR较大而FPR较小的点。模型效果越好，则ROC曲线越远离对角线。ROC曲线下的面积可以定量地评价模型的效果，记作AUC，AUC越大则模型效果越好［13］。

图2为模型一的ROC曲线。由图可看出ROC曲线凸向左上角的顶点，计算得到AUC＝0．942 963 2，接近于1，说明建立的Logistic模型一拟合效果较好，反映了量刑中区分死缓和死刑的潜在规律。

图2 模型一的ROC曲线图

第二，模型二的建立及检验（死缓或死缓限制减刑）。模型二的极大似然估计的结果如表3所示。图3为模型二的ROC曲线。由图可看出ROC曲线凸向左上角的顶点，且计算得到AUC＝0．826 079 6，接近于1，说明建立的Logistic模型二拟合效果较好，反映了量刑中区分死缓和死缓限制减刑的潜在规律。

综上，可以看到，所建立的Logistic模型很好地解释了数据的潜在规律，AUC的值最高达到0．94，由此，使用此Logistic模型对案例进行初步量刑。

2．模型预测与分析

本文使用三种案例各30例（三种判决结果各10个案例）进行预测，并计算精度，最终预测结果如表3所示。

表3 模型二参数估计和显著性检验结果表

图3 模型二的ROC曲线图

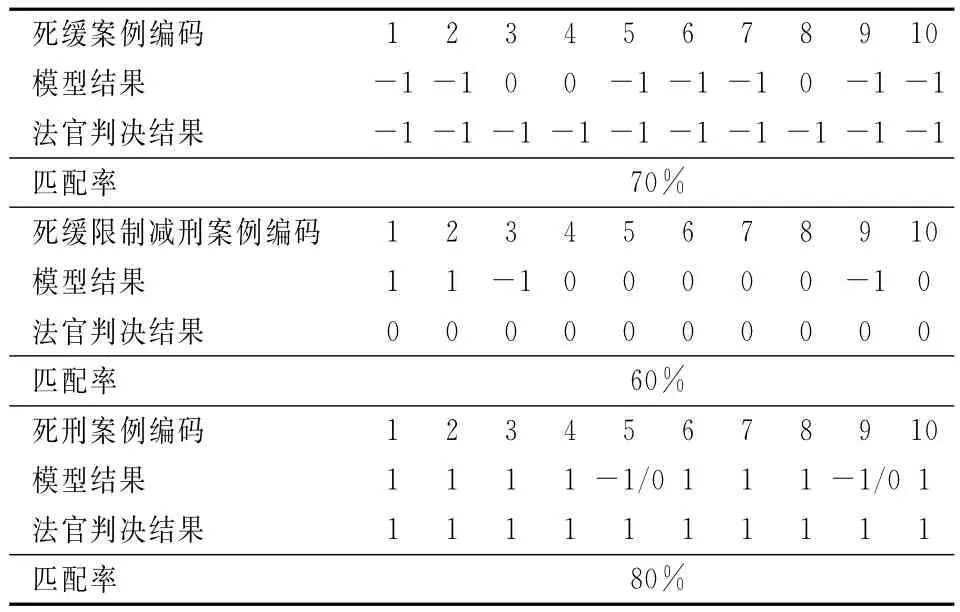
表4 模型泛化性检验表

从上表可以看出，列举的10个死缓案例中，70%的模型结果都与实际判决结果相同，剩下的30%模型结果为死缓限制减刑；10个死缓限制减刑案例中，60%的模型结果与实际判决结果相符，剩下的40%模型结果为死缓；10个死刑案例中，匹配率最高，达到80%。

研究发现，实际在法官判决过程中，死缓限制减刑与死缓的界限更加模糊，由于死刑的严重性与特殊性，这使得它与死缓限制减刑这个中间刑法界限更明确。法官判决时的人为因素和案件发生的政治社会背景差异是导致计算结果和实际判决结果不一致的部分原因，除此之外，还要考虑两种分析方法的差异，即定性分析和定量分析。运用定性与定量相结合的分析方法是最为妥善的。

四、结论与展望

为解决死缓限制减刑司法适用的疑难问题，本文系统研究讨论了Logistic函数与模型作为量刑的理论基础，并给出了构建模型的统计方法，同时结合司法案例实际数据运用Logistic回归模型对案例进行了实证分析。Logistic回归结果表明，建立的模型可以用来做法官判决的辅助工具，死刑量刑规范化的辅助手段，模型拟合结果与主观判断匹配程度可达到AUC＝94%。由于法律中变量考虑的严格不变性，并未进行变量选择，直接使用量刑过程中法官判断的标准进行回归分析，基于此发现，某些解释变量间相关程度较高，在司法实践中，法官对于死缓限制减刑适用条件的选择，属于弹性较大的裁判过程，这里面既有法律规范问题，也有刑事政策问题，甚至还存在社会学的因素，因此，建立的模型与实际判决结果存在些许差异是允许的。Logistic模型本身也存在局限性，如对线性可分的样本不可采用极大似然估计，样本的数量不宜太少，而且使用前提是自变量与因变量是线性关系，若是想要加入其它的解释变量进去，则必须考虑这一点，这是模型可以进一步改进的方向。

本文打破以往死缓限制减刑法学解释或者社科法学理论构建的研究方法，从统计学学科视角下结合实证研究方法进行交叉研究，梳理出此制度司法适用的量化研究路径，希望对公正司法、实现精密司法起到一定的参考作用，从而使刑事司法判决更加具有权威性和终局性。