考虑无形磨损的拖拉机残值系数预测模型

王 英，管延萱，冯佳欣，魏 来，宋知霖

考虑无形磨损的拖拉机残值系数预测模型

王 英，管延萱，冯佳欣，魏 来，宋知霖

（东北农业大学工程学院，哈尔滨 150030）

针对当前随着农机设备更新速度加快，无形磨损对农机折旧影响加重的问题，该文在传统拖拉机残值系数预测模型的基础上引入无形磨损系数，构建了考虑无形磨损的拖拉机残值系数预测模型。以来自于农机服务中心农机及农具拍卖结果的25台拖拉机拍卖数据为研究样本，以机龄、年平均工作时长、无形磨损系数为变量参数，分析其价值变化规律；同时，为了进一步综合对比改进模型与原模型的残值系数预测精度，引入基于几何学的“弗雷歇距离”度量法。结果表明，改进模型与原模型相比，预测偏差较小，预测精度大幅度提高，达到24.9%及以上，能够显著地提高拖拉机残值预测准确度，该研究为折旧成本的计算和农机设备的更新决策提供了科学、准确的决策依据。

农业机械；模型；磨损；拖拉机；残值系数；弗雷歇距离

0 引 言

在农业机械化生产中，折旧是设备使用过程中由于机器磨损、技术落后、使用时间等原因造成的价值损耗，在农业机器作业成本中占有很大比重。科学合理的折旧应以正确估计机器设备的残值为基础，才能保证成本计算的准确性和农机系统优化决策的科学性。

关于农机折旧的理论研究一直较少，更多的集中在资产重估[1-3]和折旧方法方面[4-6]。目前国内外折旧方法主要包括直线法、年数总和法、定值递减法[7]、余额递减法、双倍余额递减法[8]等，经过综合研究表明动态余额递减法是目前最能反映机器价值变化规律的折旧模型[9-10]。但是不同农业机器的实际价值转移规律具有很大的差异性，具体用哪一种折旧方法和采取多少折旧比例来计算某一种农业机器的折旧成本，一直是困扰管理工作者的难点，也直接影响折旧额的科学性和合理性[11-13]。农机折旧成本计算的要素包括残值和折旧年限，若建立残值系数模型，则能够更加科学地估计不同机龄、不同类型的农业机器折旧成本[14-17]。现有的ASABE（American Society of Agricultural and Biological Engineers）农机通用残值系数模型是以公开拍卖的机器数据为基础，通过回归分析方法建立了12种不同农机的残值函数表达式[18-19]。但是由于该模型的基础数据来自于美国生产实践，而农业机器的残值与其制造水平、作业条件、维修保养等诸多因素有关，因此该模型并不适用于中国实际情况，建模思想可以学习，但模型不能照搬[20]。小型拖拉机的残值预测模型是国内较早建立的残值模型，但是忽略了不同拖拉机年平均工作时间的差异性和不同年份资金的时间价值，忽略了无形磨损的影响，因此模型精度不高[21-23]。

一直以来，对于农机残值的研究大多考虑的是有形磨损因素，但是随着科技进步，劳动生产率提高，无形磨损速度也随之加快。因此，农机残值的预测需要将有形磨损和无形磨损有机结合。本文将对2种磨损类型进行量化分析，并以此为基础，建立拖拉机残值系数预测模型。

1 设备磨损类型及量化分析

1.1 有形磨损

有形磨损亦称物理磨损，是指设备在使用或闲置期间发生的物理变化或化学侵蚀，可分为2种类型：第1种有形磨损是指设备在使用过程中产生的损耗，如因摩擦、振动、疲劳等导致的损耗、意外损耗、故障维修；第2种有形磨损是设备在闲置过程中受环境影响造成的损耗，如：氧化生锈、腐蚀、老化等。这2类有形磨损无疑直接导致了设备性能减弱、精度降低，同时提高了作业及维修成本，从而间接导致设备的使用价值大幅降低。

1.2 有形磨损量化分析

一直以来，对于农机装备磨损程度评价主要考虑的是工作量、燃油消耗、维修费用等因素。因此，对于某一机龄的某种机器的磨损程度评价对应的是一个多元指标集，但是最终都归结于机器本身残值的降低。现有的残值预测模型均只考虑了有形磨损的影响，因此对于有形磨损量化的研究就是对残值系数模型的研究。

美国ASABE通过大量试验给出了农机通用残值系数模型，即

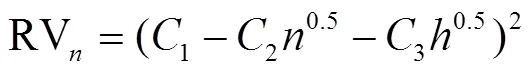
式中RV为农业机器第年的残值系数，即为折现后农业机器第年的残值与其原值之比；1、2、3为ASABE残值系数模型的系数，取值如表1所示；为农业机器的预计使用年限，a；为设备年平均作业时长，h。

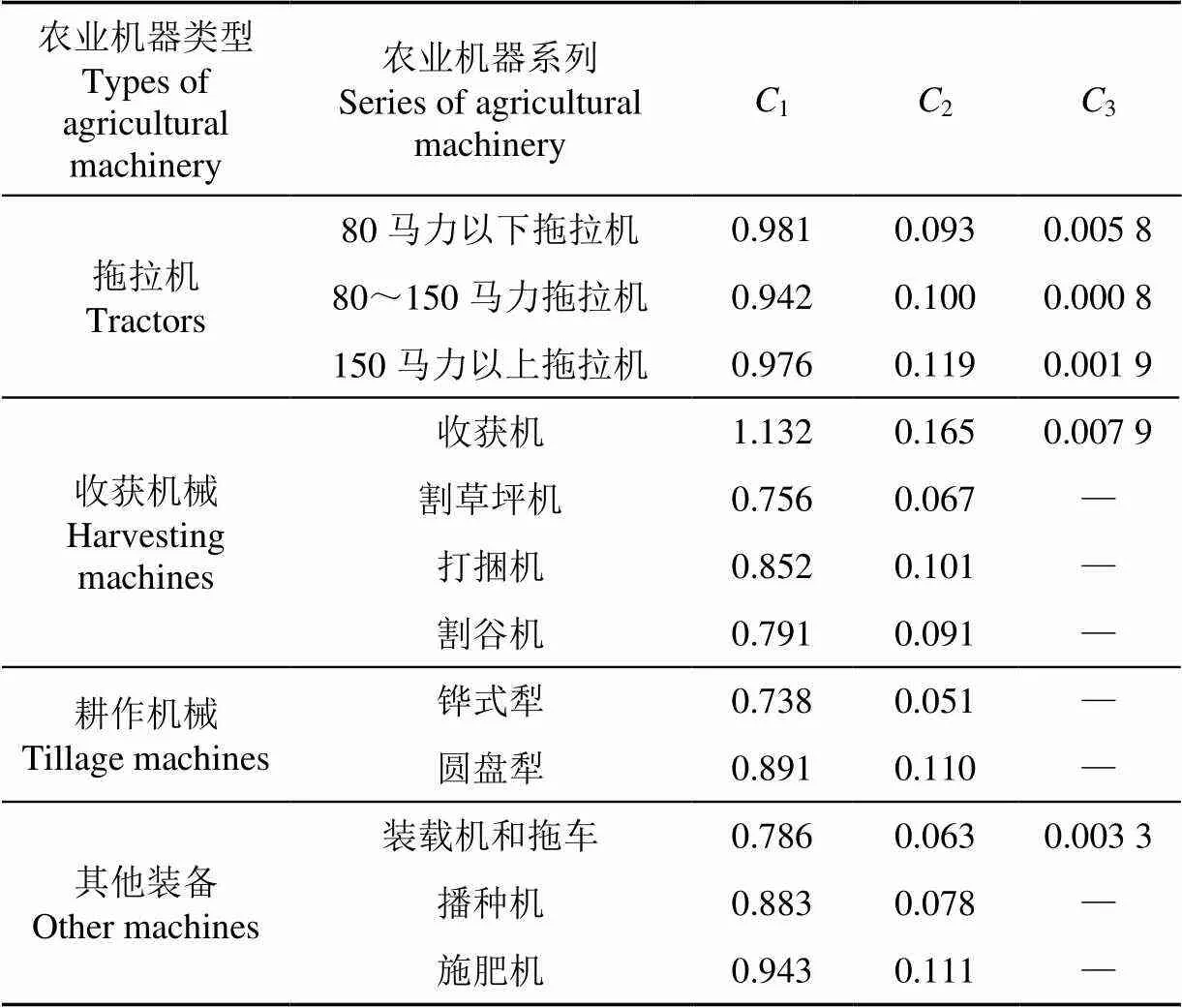
表1 ASABE残值模型系数

ASABE模型的建立是基于美国的农业现状和气象数据，由于地理环境、经济水平、人文基础以及农业生产的差异性导致了中美两国农业发展有很大不同，因此适用于美国的很多技术参数在中国环境条件下会发生较大改变。

文献[24]以江苏省大丰市上海农场的81台大中型拖拉机公开拍卖数据为基础，主要考虑机器的机龄和年平均作业时长两大因素，对ASABE农机通用残值系数模型进行改进，对自变量和因变量进行不同的Box-Cox变换，得到了范围更广的6种不同类型的残值系数函数形式，并通过回归分析和数据检验，优选了适合国内大中型拖拉机的残值预测模型，即双平方根残值模型

式中为拖拉机残值系数；1为机龄，a；2为年平均作业时长，h。

前期研究发现，当拖拉机机龄超过4 a时，该模型对于残值系数预测的精度大幅降低，主要原因是随着拖拉机使用时间的增长，机器残值受无形磨损，即技术进步的影响逐渐增强[25]。

因此，在当前主要研究有形磨损对拖拉机残值影响的基础上，本文将进一步研究无形磨损对拖拉机残值的影响，对上述模型进行改进。

1.3 无形磨损

无形磨损又称经济磨损，是指设备由于科学技术进步或市场需求变化而引起的价值贬值，不是因设备使用或自然力作用导致的，而是技术进步的结果。无形磨损可分为2种类型：第1种无形磨损是随着技术进步和社会劳动生产率水平的提高，同类设备的再生产价值降低，导致原设备相应贬值；第2种无形磨损是由于科技进步和技术创新，农机制造企业生产出更加完善高效的设备，相比较之下原设备技术性能逐渐落后，经济效益降低[26-27]。

1.4 无形磨损量化分析

由技术进步所导致的无形磨损缩短了设备最佳使用寿命，已成为驱动设备更新的重要影响因素[28-29]。近些年，一些学者通过假设技术进步速率已知或呈指数分布，构建了设备更新决策模型，探讨考虑无形磨损情况下设备更新周期的变化[30-32]。技术进步或无形磨损主要表现为原机器设备的价值贬值，运行与维修费用的增加和经济效益的下降[33-35]，因此，关于无形磨损及其严重程度则主要考虑经济上是否合理。针对1.3节的2种无形磨损情况，分别进行量化。

1）劳动生产率提高导致的无形磨损量化模型为

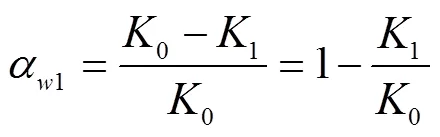
式中α1为第1种无形磨损程度；0为机器原始价值，元；1为机器目前价值，元。

2）高效设备出现导致的无形磨损量化模型为

式中为α2第2种无形磨损程度；C为新机器单位作业成本，元；0为原机器单位作业成本，元。

因此，无形磨损综合程度α为

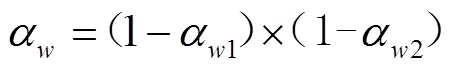
2 拖拉机残值系数预测模型构建

大中型拖拉机残值与诸多因素有关，如使用年限、作业时长、交易手段及经济效益等。因此，在不降低模型计算精度的前提下，为方便计算应筛选出主要变量。依据文献[20，36-37]的研究，本文将选择机龄、年平均作业时长和无形磨损程度作为主要变量进行研究，与此同时，考虑资金的时间价值。残值系数的本质含义和函数形式如式（6）、式（7）所示。

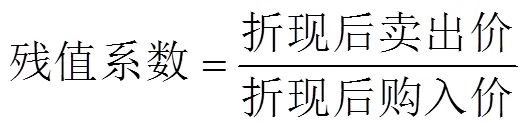
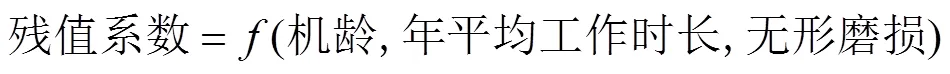
2.1 建模假设

拖拉机残值系数预测模型建模假设如下：

1）残值系数及其相关变量之间相互独立；

2）模型的自变量为机龄、年平均工作时长和无形磨损程度；

3）通过公开拍卖方式得到的农机设备数据可以体现其真实价值变化规律。

2.2 试验数据获取

试验数据来自于农机服务中心农机及农具拍卖结果公示，相比二手交易市场复杂的交易环境，通过公开拍卖方式得到的农机设备数据能够更真实地表示当时条件下的拖拉机真实价值。为了计算准确性，引入折现系数。折现系数是货币单位复利值的倒数，将不同年份的现金流量通过折现系数得到需要的客观现值。为排除货币时间价值的影响，将样本数据中不同年份机器设备的购入价与卖出价均折现到同一时间点。本文选取样本数据中机器买入时间最早的时间节点，即2010年3月，则通过折现系数将所有农机购入和卖出金额均折现到2010年3月。由于每年银行利率可能会进行多次调整，则年利率按照平均年利率计算，各年平均年利率见表2，即可得到表3中机器设备购入年和卖出年的资金折现系数；并按照式（6）可计算出各机器设备的残值系数。

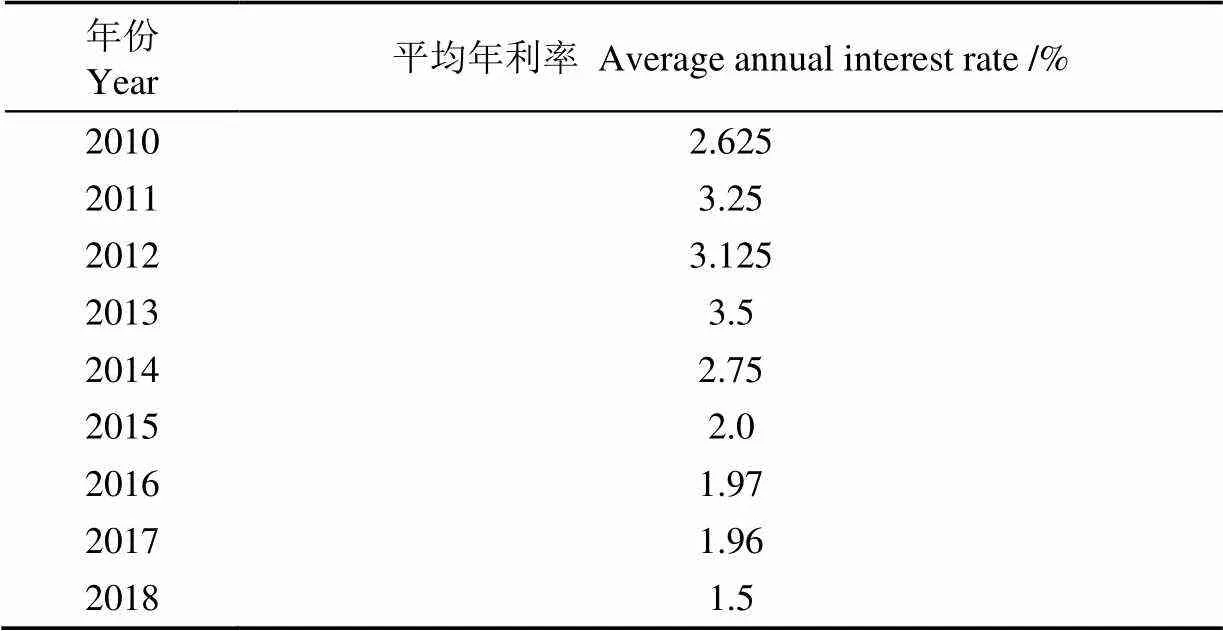
表2 银行不同年份平均年利率

注：数据来源中国统计摘要人民币一年期存贷款利率。Note: The data source is from China statistical abstract CNY one-year deposit and loan interest rate.

样本数据如表3所示，其中，观察样本共有25台轮式拖拉机；机龄以卖出时间与购买时间的实际差值来计算；拖拉机的年平均作业时长则以拍卖时上报的总工作时长与机龄之比来计算[38]。从表3中可知，25个轮式拖拉机的机龄4～8 a，年平均工作时长232～720 h不等。

表3 研究样本基本数据

注：数据来源农机服务中心农机及农具拍卖结果公示。

Note: The data source is from the announcement of the auction results of agricultural machinery and farm tools in the Agricultural Machinery Service Center.

2.3 构建残值系数预测模型

通常计算设备折旧是采用预估折旧费用的方式，计算方法是设备原值乘以残值系数。国内外诸多学者通过大量的数据研究得到机器残值系数的变化趋势是随着机器年平均作业时长和机龄的增加而下降。文献[24]通过回归分析、残差分析得到了相对准确的拖拉机残值系数预测模型，如式（2）所示，并用于预测中国大中型拖拉机的残值，且预测精度较高。但该模型存在的问题是对机龄3～4 a的拖拉机残值系数预测精度较高，当拖拉机使用机龄超过4 a，模型预测精度明显降低，主要原因是随着拖拉机使用时间的增长，其价值受无形磨损的影响逐渐增强。因此，为了提高拖拉机残值系数的预测精度，应在现有预测模型基础上，考虑无形磨损对拖拉机残值的影响。

假设现有的拖拉机残值系数预测模型与无形磨损系数相乘，模型的预测精度会得到提高，则改进的拖拉机残值系数预测模型如式（8）所示。

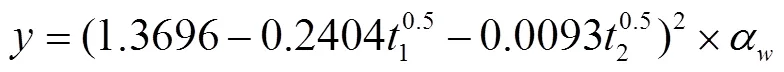
式中为拖拉机残值系数；1为机龄，a；2为年平均作业时长，h。

下面将通过样本数据来验证上述假设：首先，利用式（5）计算表3中25台拖拉机样本的无形磨损综合程度；然后，通过式（2）和式（8）分别计算原有模型和改进模型的残值系数预测值；最后，将原有模型和改进模型的残值系数预测值与残值系数的实际值进行比较，具体结果如表4所示。

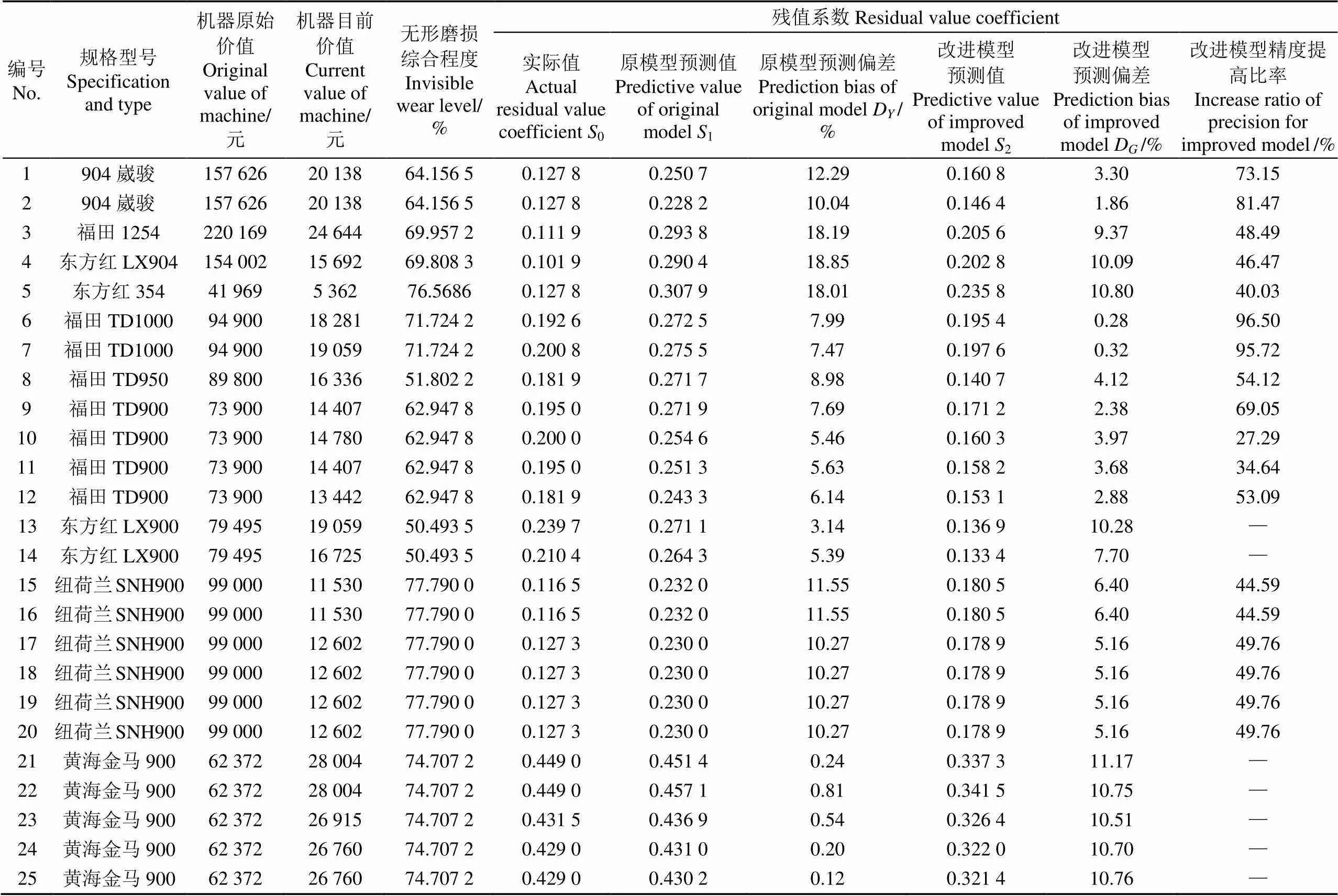
表4 改进模型与原模型预测结果对比

注：表中机器原始价值＝机器买入价格×买入时间折现系数；机器目前价值＝机器拍卖价格×卖出时间折现系数；原模型预测偏差D＝︱1－0︱×100；改进模型预测偏差D＝︱2－0︱×100；改进模型精度提高比率＝(D－D)×100／D；“－”表示改进模型精度没有提高。

Note: Primitive value of machine＝Buying price of machine×Discount coefficient of buying time; Current value of machine＝Auction price of machine×Discount coefficient of buying time; Prediction bias of original modelD＝︱1－0︱×100;Prediction bias of improved modelD＝︱2－0︱×100; Increase ratio of precision for improved model＝(D－D)×100／D; “－” denotes no increase of precision for improved model.

根据表4，对于1～20号机型（除13和14号机型外），使用改进模型计算得到的残值系数更接近于实际残值系数，同原模型相比，其预测偏差较小，预测精度得到大幅度提高（达到27%以上）；而对于21～25号机型，原模型残值系数预测值与实际残值系数更为接近，改进模型的预测偏差较大，预测效果不理想。这是由于21～25号机型的机龄为4 a以内，1～20号机型的机龄均在5 a以上，由此可见，农机在使用初期，由于技术变化不大，其受无形磨损影响较小；但是随着农机机龄的增长，科学技术不断发展和进步，一方面设备制造工艺的改进和社会劳动生产率的提高使同类设备的再生产价值降低，另一方面技术更先进、性能更完善、生产效率更高、原材料和能源消耗更低的新型设备将会出现，则无形磨损对农机残值的影响会逐渐体现，并日益增强。因此，对于使用年限相对较长的农机残值预测，必须考虑技术进步导致的无形磨损带来的影响。

2.4 模型验证

为了进一步综合对比原模型与改进模型的残值系数预测精度，引入基于几何学的“弗雷歇距离”度量法，根据基于弗雷歇距离定义的相似度函数，分别计算原模型和改进模型曲线与实际残值系数曲线的相似度，相似度最大的曲线所对应的模型即为最优。该方法无需大量的训练样本，且具有较高的准确率和识别度[39]。

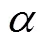
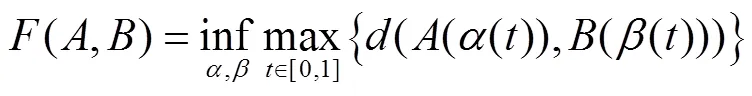
式中为上的度量函数；为变量，且∈[0，1]。

根据弗雷歇距离的思想，采用弗雷歇距离算法来刻画2条曲线之间的距离，即弗雷歇距离，具体操作如下：

4）分别计算和上各样本点到上各样本点的距离，得到距离矩阵D、D

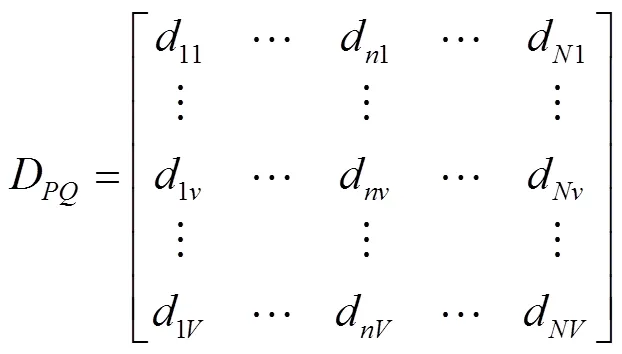
式中d为曲线上的第个样本点到曲线上第个样本点的距离，计算公式如下

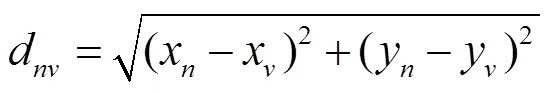
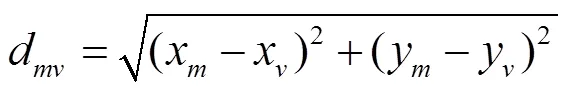
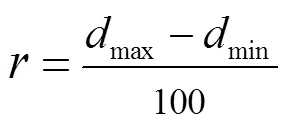
6）将距离矩阵D和D中小于或等于各自min的元素设为1，大于min的元素设为0，即可得到2个二值矩阵。

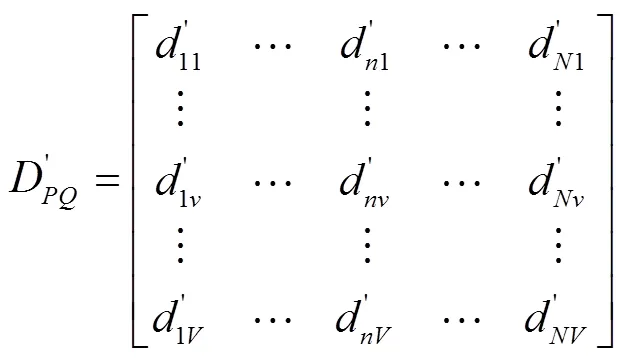
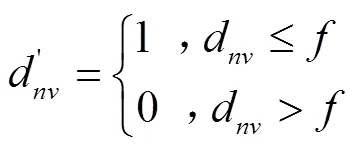
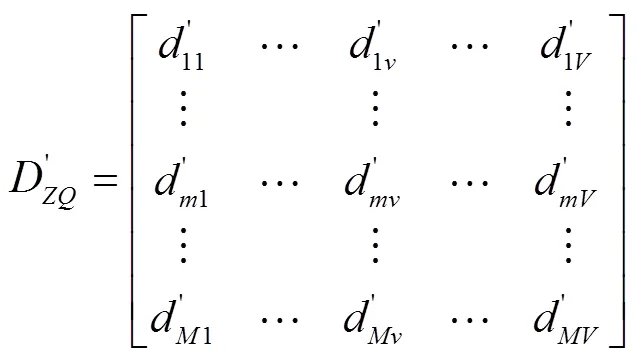
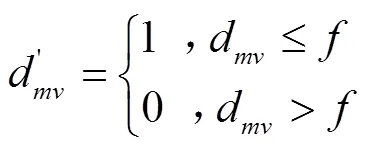
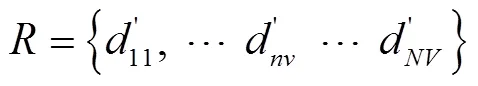
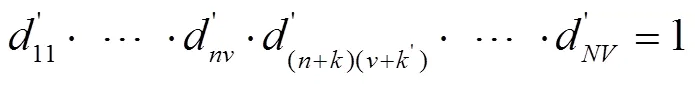
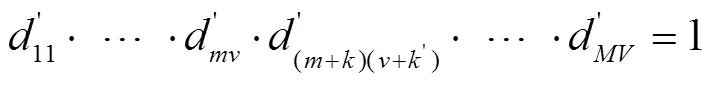
根据以上步骤，通过Matlab编程实现计算过程，比较曲线和与的弗雷歇距离，即计算原模型曲线、改进模型曲线与实际残值系数曲线的相似度，弗雷歇距离越小，相似度越大，所对应的模型即为最优。计算结果如表5所示。

表5 残值系数预测模型曲线相似度计算结果

通过弗雷歇距离可以得到2条曲线点集之间的距离，距离越小，说明2条曲线之间的相似程度越高。由表5可知，与原模型相比，改进模型的残值系数预测曲线与实际残值系数曲线的弗雷歇距离更小，说明改进模型的残值系数预测值与实际残值系数的相似程度更大，即预测的准确度更高。

根据弗雷歇距离的意义，改进模型相对于原模型预测精度的提高程度可通过弗雷歇距离的降低程度来表示，即

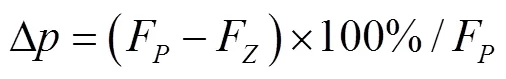
将表5中相应数据带入式（20）得：改进模型相对于原模型的预测精度提高了24.9%。

通过改进模型验证和弗雷歇距离度量法验证，表明改进模型具有更高的预测精度和预测准确度，因此，可用改进模型来预测拖拉机的残值，以得到更为满意的预测结果。

3 结 论

1）对于由于劳动生产率提高和科技进步导致的2种无形磨损，分别建立了量化模型，模型简便易操作，推广性强，不仅可用于成本效益分析，同时可以拓展到农机设备更新决策研究。

2）随着农机机龄的增长，科学技术不断发展和进步，无形磨损对农机残值的影响逐渐增强，农机残值系数预测必须考虑无形磨损的影响。

3）以美国ASABE残值系数模型、机龄和年平均作业时间双平方根模型为基础，引入无形磨损系数，采集来自于农机服务中心及农具拍卖结果的25台轮式拖拉机拍卖数据作为研究样本，对已有的残值系数预测模型进行了改进。结果显示，同原模型相比，改进模型得到的残值系数预测值更接近残值系数的实际值，其预测偏差较小，预测精度得到了大幅度提高，达到27%以上。

4）根据基于弗雷歇距离定义的相似度函数，综合评价原模型与改进模型对残值系数的预测精度。结果表明，改进模型具有较高的预测精度，能够更好地提高拖拉机残值预测的准确度。

本文研究仍存在不足之处，由于市场上经过公开拍卖的农机数据较少，不同机龄的样本数量有限，该项因素可能会影响模型的精度。

[1] Liapis K J, Kantianis D D. Depreciation methods and life-cycle costing (LCC) methodology[J]. Proedia Economics and Finance, 2015, 19: 314－324.

[2] Kupper H U, Pedell B. Which asset valuation and depreciation method should be used for regulated utilities? An analytical and simulation-based comparison[J]. Utilities Policy, 2016, 40: 88－103.

[3] 唐恒书，刘俊秀，程余圣鸿. 固定资产折旧模式与企业价值研究[J]. 会计之友，2018(20)：112－114. Tang Hengshu, Liu Junxiu, Cheng Yushenghong. Research on depreciation model and enterprise value of fixed assets[J]. Friends of Accounting, 2018(20): 112－114. (in Chinese with English abstract)

[4] Keil J. Depreciated depreciation methods? Alternatives to sraffa’s take on fixed capital[J]. Review of Political Economy, 2016, 28(4): 566－589.

[5] 王奕娇，乔金友，任国强，等. 农业机器折旧方法研究[J]. 农机化研究，2016，38(7)：129－132. Wang Yijiao, Qiao Jinyou, Ren Guoqiang, et al. The reasearch on depreciation methods of agricultural machinery[J]. Journal of Agricultural Mechanization Research, 2016, 38(7): 129－132. (in Chinese with English abstract)

[6] Jennergren L P. A note on the linear and annuity class of depreciation methods[J]. International Journal of Production Economics, 2018, 204: 123－134.

[7] 董国荣. 一种新的农机折旧计算方法—定值递减法[J]. 农业机械学报，2000，31(4)：120－121. Dong Guorong. A new method for calculating depreciation of agricultural machinery——the method of definite value decreasing[J]. Transactions of the Chinese Society for Agricultural Machinery, 2000, 31(4): 120－121. (in Chinese with English abstract)

[8] 王福林. 农业机器折旧中的双倍余额递减法改进研究[J]. 农业机械学报，2003，34(4)：66－67. Wang Fulin. Improvement of double diminishing method for farm machine depreciation[J]. Transactions of the Chinese Society for Agricultural Machinery, 2003, 34(4): 66－67. (in Chinese with English abstract)

[9] 朱亚东. 黄海农场农业机器选型与配备的研究[D]. 南京：南京农业大学，2009. Zhu Yadong. Study on Selection and Allocation of Agricultural Machinery in Huanghai State Farm[D]. Nanjing: Nanjing Agricultural University, 2009. (in Chinese with English abstract)

[10] 汤二征，何瑞银. 大中型拖拉机折旧方法选择的研究[J]. 江苏农机化，2010(1)：32－34. Tang Erzheng, He Ruiyin. Study on depreciation method selection of large and medium-sized tractors[J]. Jiangsu Agricultural Mechanization, 2010(1): 32－34. (in Chinese with English abstract)

[11] Wilson P. Estimating tractor depreciation: the impact of choice of functional form[J]. Journal of Farm Management, 2010, 13(12): 799－818.

[12] 王奕娇，乔金友，任国强，等. 农业机器折旧决策支持系统的研究与设计[J]. 农机化研究，2016，38(1)：106－108. Wang Yijiao, Qiao Jinyou, Ren Guoqiang, et al. The research and design on decision support system for agricultural machinery depreciation[J]. Journal of Agricultural Mechanization Research, 2016, 38(1): 106－108. (in Chinese with English abstract)

[13] 张馨璐，张义. 企业固定资产折旧方法对企业财务影响[J]. 商场现代化，2016(7)：190－191. Zhang Xinlu, Zhang Yi. Study on the influence of depreciation method of fixed assets on enterprise finance[J]. Market Modern, 2016(7): 190－191. (in Chinese with English abstract)

[14] Dumler T J, Burton R O, Kastens T L. Predicting farm tractor values through alternative depreciation methods[J]. Review of Agricultural Economics, 2003, 25(2): 506－522.

[15] Guadalajara-Olmeda N, Fenollosa-Ribera M L. Valuation models of agricultural machinery in southern Europe. An analysis of real depreciation[J]. Agrociencia, 2010, 44(3): 381－391.

[16] Smolyak S A. Models for estimating depreciation in plants, machinery, and equipment: Analysis and proposals[J]. Journal of Property Tax Assessment and Administration, 2012, 9(3): 47－73.

[17] Sahu A K, Narang H K, Sahu A K, et al. Machine economic life estimation based on depreciation-replacement model[J]. Cogent Engineering, 2016, 3(1): 1－15.

[18] Cross T L, Perry G M. Remaining value functions for farm equipment[J]. Applied Engineering in Agriculture, 1996, 12(5): 547－553.

[19] Agricultural Machinery Management Data: ASAE standards D497.5[S]. St. Joseph, Mich: ASABE, 2006.

[20] 何瑞银，王耀华，马培刚，等. 大中型拖拉机残值模型的研究[J]. 农业工程学报，2008，24(5)：131－135. He Ruiyin, Wang Yaohua, Ma Peigang, et al. Model for remaining value function of the large and medium-sized tractors in China[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2008, 24(5): 131－135. (in Chinese with English abstract)

[21] Hansen L R, Lee H. Estimating farm tractor depreciation: tax implications[J]. Canadian Journal of Agricultural Economics/Revue Canadienne Dagroeconomie, 1991, 39(3): 463－479.

[22] 吴建民. 小型拖拉机最佳更新期的动态研究[J]. 农业工程学报，1998，14(2)：78－81. Wu Jianmin. The dynamic study on optimum renewal opportunity of the small tractors[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 1998, 14(2): 78－81. (in Chinese with English abstract)

[23] Bobby Himawan. Analisis Perhitungan Cost Pengelolaan Sampah Dan Pelaporan Keuangan[D]. Yogyakarta: Universitas Gadjah Mada, 2018.

[24] 何瑞银. 农业机器系统优化模型与水稻种植区典型系统评价的研究[D]. 南京：南京农业大学，2008. He Ruiyin. Study on the Optimization Model of Farm Machinery System and the Evaluation of Typical Systems in Paddy Regions[D]. Nanjing: Nanjing Agricultural University, 2008. (in Chinese with English abstract)

[25] 吴媞，刘鹏飞，张小龙. 拖拉机经济性虚拟综合测试系统设计与试验[J]. 农业机械学报，2016，47(3)：117－123. Wu Ti, Liu Pengfei, Zhang Xiaolong. Design and field test of integrated virtual test system for tractor economy performance[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(3): 117－123. (in Chinese with English abstract)

[26] 刘义乐，伍书剑，徐宗昌. 无形磨损对产品技术寿命的影响[J]. 中国船修，1995(5)：37－39. Liu Yile, Wu Shujian, Xu Zongchang. The influence on product technical life span of invisible wear and tear[J]. China Shiprepair, 1995(5): 37－39. (in Chinese with English abstract)

[27] 谢斌，武仲斌，毛恩荣. 农业拖拉机关键技术发展现状与展望[J]. 农业机械学报，2018，49(8)：1－17. Xie Bin, Wu Zhongbin, Mao Enrong. Development and prospect of key technologies on agricultural tractor[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(8): 1－17. (in Chinese with English abstract)

[28] Schochetman I E, Smith R L. Infinite horizon optimality criteria for equipment replacement under technological change[J]. Operations Research Letters, 2007, 35(4): 485－492.

[29] Emmanuel D, Esra B I. Optimizing capital investments under technological change and deterioration: A case study on MRI machine replacement[J]. Engineering Economist, 2017, 62(2): 105－131.

[30] Hritonenko N, Yatsenko Y. The dynamics of asset lifetime under technological change[J]. Operations Research Letters, 2008, 36(5): 565－568.

[31] Motamedi N, Peyghami R, Hadizadeh M. A mixed integer nonlinear programming model for the optimal repair-replacement in the firm[J]. Mathematical Social Sciences, 2013, 66: 366－370.

[32] Yatsenko Y, Hritonenko N. Machine replacement under evolving deterministic and stochastic costs[J]. International Journal of Production Economics, 2017, 193: 491－501.

[33] 王英，方淑芬，吕文元. 技术进步条件下设备经济寿命分析[J]. 东北农业大学学报，2007，38(2)：85－88. Wang Ying, Fang Shufen, Lv Wenyuan. Analysisi on economic life of equipment under technological progress[J]. Journal of Northeast Agricultural University, 2007, 38(2): 85－88. (in Chinese with English abstract)

[34] Hritonenko N, Yatsenko Y. Economic life replacement under improving technology[J]. International Journal of Production Economics, 2011, 33: 596－602.

[35] Yatsenko Y, Hritonenko N. Algorithms for asset replacement under limited technological forecast[J]. International Journal of Production Economics, 2015, 160: 26－33.

[36] 常征. 水稻产区农业机械优化配备及产业化经营模式研究[D].哈尔滨：东北农业大学，2003. Chang Zheng. Study on Optimization and Equipment and Industry Management Model of Agricultural Machinery in Paddy Region[D]. Harbin: Northeast Agricultural University, 2003. (in Chinese with English abstract)

[37] 李中才. 农业机器系统状态仿真及更新决策的研究[D]. 哈尔滨：东北农业大学，2005. Li Zhongcai. Study on the State Transfer Simulating and Replacement Decision of Agricultural Machinery System[D]. Harbin: Northeast Agricultural University, 2005. (in Chinese with English abstract)

[38] 王福林，石光辉，王吉权. 拖拉机技术经济指标的获取与处理方法[J]. 农业机械学报，2006，37(6)：76－78. Wang Fulin, Shi Guanghui, Wang Jiquan. Study on the method of getting and dealing with some technical and economic indexes of tractor[J]. Transactions of the Chinese Society for Agricultural Machinery, 2006, 37(6): 76－78. (in Chinese with English abstract)

[39] 黄世泽，陈威，张帆，等. 基于弗雷歇距离的道岔故障诊断方法[J]. 同济大学学报：自然科学版，2018，46(12)：1690－1695. Huang Shize, Chen Wei, Zhang Fan, et al. Method of turnout fault diagnosis based on fréchet distance[J]. Journal of Tongji University: Natural Science, 2018, 46(12): 1690－1695. (in Chinese with English abstract)

Prediction model of tractor residual value coefficient considering factor of invisible wear

Wang Ying, Guan Yanxuan, Feng Jiaxin, Wei Lai, Song Zhilin

(,,150030,)

Depreciation takes up a large proportion in the total activity cost of agricultural machinery. As the update speed of agricultural machinery was gradually accelerating, the impact of the invisible wears was strengthened by technological progress on agricultural machinery depreciation. Aiming to this problem, two types of invisible wears, which were caused by increased labor productivity and the emergency of more advanced machines, were analyzed and quantified respectively, and based on which, the comprehensive invisible wear degree was given in this paper. According to the traditional ASABE (American Society of Agricultural and Biological Engineers) residual value coefficient prediction model of tractors, considering the invisible wear factor, an improved prediction model of the residual value coefficient for tractors was established. Based on the auction data of 25 wheeled tractors collected from the agricultural machinery and tools auction results in the agricultural machinery service center, the age, the average annual working hours and the comprehensive degree of the invisible wears were used as the main independent variables to construct the improved model of the tractor residual value coefficient prediction and to analyze the law of the tractor value change. In addition, in order to increase the calculation accuracy, the discount coefficient was introduced to consider the time value of the capital. The results showed when the tractor age was above five years, the prediction value of the improved model was closer to the real residual value coefficient, and compared with the original model, the improved model was with less prediction deviation and higher prediction precision that was improved by more than 27%; but when the tractor age was within four years, the prediction deviation for the improved model was bigger than the original model, and the prediction result of the improved model was not satisfactory. The main reasons causing the results were that the effect of the invisible wears on the tractor was very small due to smaller technological progress in its early working period, but with the increasing of the tractor age and the development of science and technology, on one hand, the reproduction value of the same type of tractor would go down because of the improvement of manufacturing process and the increase of social labor productivity; on the other hand, the new type of machines, which were with more advanced technology, better performance, higher productivity and lower consumptions of raw materials and energy, would occur, so the effect of the invisible wears on the tractor residual value would intensified gradually, which also demonstrated that when predicting the residual value of agricultural machinery used for a relatively long period of time, the influence of the invisible wears must be considered. At the same time, the method of the geometry-based “Fréchet distance” metric was applied to further comprehensively compare and evaluate the prediction accuracies of the original model and the improved model. The results showed that compared with the original model, the improved model was with the higher prediction precision that was improved by 24.9%, and was able to significantly improve the accuracy of residual value prediction of tractors. The research of this paper can provide scientific and accurate decision-making basis for the calculation of depreciation cost and the determination of replacement time of agricultural machinery.

agricultural machinery; model; wear; tractors; residual value coefficient; Fréchet distance

10.11975/j.issn.1002-6819.2019.17.008

S232

A

1002-6819(2019)-17-0058-08

2019-05-20

2019-07-06

十三五科技部国家重点研发计划项目“黑龙江半湿润区粳稻全程机械化丰产增效技术体系集成与示范”（2018YFD0300105-6）

王英，博士，教授，博士生导师，主要从事农业机械化生产与管理研究。Email：angelbabywan@163.com

王 英，管延萱，冯佳欣，魏 来，宋知霖. 考虑无形磨损的拖拉机残值系数预测模型[J]. 农业工程学报，2019，35(17)：58－65. doi：10.11975/j.issn.1002-6819.2019.17.008 http://www.tcsae.org

Wang Ying, Guan Yanxuan, Feng Jiaxin, Wei Lai, Song Zhilin. Prediction model of tractor residual value coefficient considering factor of invisible wear[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(17): 58－65. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.17.008 http://www.tcsae.org

中国农业工程学会会员：王英（E040500008M）