水轮机调速器功率调节模式下负荷调节过渡过程稳定性研究

鲍海艳，龙丽婷，付 亮，魏加富

水轮机调速器功率调节模式下负荷调节过渡过程稳定性研究

鲍海艳1，龙丽婷1，付 亮2，魏加富2

（1. 长沙理工大学水利工程学院，长沙，410114；2. 国网湖南省电力有限公司电力科学研究院，长沙，410007）

作为电力系统中调峰调频的骨干电源，水电机组负荷调节过渡过程稳定性对电网安全运行及源网协调意义重大。该文采用理论分析及数值仿真的方法对水轮机调速器功率模式下负荷调节过渡过程的稳定性进行了深入分析，得出了以调速器参数为变量的机组运行稳定域，并推导出满足稳定性的判别式。分析了水流惯性、接力器响应特性以及水轮机特性对稳定域的影响，得出水流惯性不利于系统的稳定，而接力器响应特性对系统稳定性有利，及水轮机特性最不利工况为水轮机综合特性系数与水轮机传递系数e乘积值最大处。该文的研究成果能够准确地找到负荷调节稳定性的最不利工况，有效的指导水轮机调速器功率模式下参数整定，保障水电机组的稳定运行。

水电站；水轮机；功率模式；负荷调节；稳定性；调速器参数

0 引 言

目前中国电力系统已基本形成了以特高压为骨干网架的交直流混联电网，随着大量的风电、太阳能等间歇性能源投运，电网的安全稳定问题愈加突出。作为电力系统中调峰调频的骨干电源，水电机组负荷调节过渡过程的稳定性及调节品质直接影响到了电网的安全及网源协调[1-4]。

为维持电网频率的稳定及功率的平衡，电网调度部门通过自动发电控制系统（automatic generation control）实时向水电厂计算机监控系统下达目标负荷调节指令，水电机组接受到AGC负荷调节指令后自动调节机组有功功率[5]，对于已投入AGC的水电机组每天的负荷调节次数非常频繁，如凤滩水电厂日调节次数就超过了2 000次[6]。目前水轮机调速器负荷调节主要有2种模式：开度模式和功率模式[7]。相比开度模式，功率模式下监控系统只需下发功率目标值，由调速器自动完成功率闭环调节，其响应快且能够实现一次调频与AGC的协调控制，已在很多大型水电机组中得到应用。由于水轮机调节系统“水锤效应”及水轮机非线性参数时变的特性，水电机组功率调节性能十分复杂，一旦控制参数设置不当就容易恶化负荷调节性能甚至出现功率振荡，严重危及电网安全[8-10]。特别是对于水电比例相对较高的区域电网，水电机组本身的功率振荡易诱发电网的低频振荡[11-17]，因此电网调度部门对水电机组参与AGC调节的性能极为重视，各区域电网均出台了相应的考核办法，同时也建立了电网低频振荡预警系统，对水电机组功率调节过程中出现的失稳及功率振荡进行预警并进行严格控制[18]。

目前对于水轮机调速器功率模式下负荷调节过渡过程的研究主要集中在控制逻辑、试验仿真以及控制参数优化三个方面。文献[19]分析了功率调节模式的直接式和间接式调节结构及其实现方法，并在此基础上提出了功率调节的适应式变参数策略及其在水电厂AGC系统中的应用情况。文献[20]提出了一种基于自适应PID控制的水电站有功功率调节。文献[21]提出了基于三段速度调节方式的功率反馈调节模式。文献[22]对带变顶高尾水洞水电机组调速器功率模式下负荷调节及一次调频进行了仿真和试验，优化了控制参数。文献[23]提出了一种改进型控制结构结合增量式PID算法的功率调节控制逻辑。文献[24]对调速器功率模式下一次调频试验方法进行了探讨。

综上所述，目前的研究成果中对于调速器功率模式调节过程中稳定性问题很少涉及，而实际有多个水电厂在运行过程中就曾出现过调速器功率模式下失稳的问题，导致了功率的振荡，影响了电网的正常运行及网源协调[25-26]。本文试图采用理论分析及数值仿真的方法对水轮机调速器功率模式下负荷调节过渡过程稳定性进行深入分析，得到调速器功率模式下调节稳定域，分析水锤现象、水轮机特性、调速器响应特性对稳定域的影响，提出调速器参数优化方法从而控制功率振荡的风险。

1 基于弹性水击模型的数值分析

1.1 数学模型

水电机组负荷调节过程中并大网运行，此时认为机组转速无变化，因此其调节原理如图1所示，各子系统数学模型如下所示。

注：Kp、KI、KD为水轮机调速器参数，其中Kp为比例增益，KI为积分增益，KD为微分增益；Ty为接力器响应时间常数，s；ey为水轮机转矩对导叶开度的传递系数；eh为水轮机转矩对水头的传递系数；eqy为水轮机流量对导叶开度的传递系数；eqh为水轮机流量对水头的传递系数；s为拉普拉斯算子。

引水管道数学模型：忽略水头损失，采用弹性水击模型，变量取相对偏差形式并利用拉氏变换可得

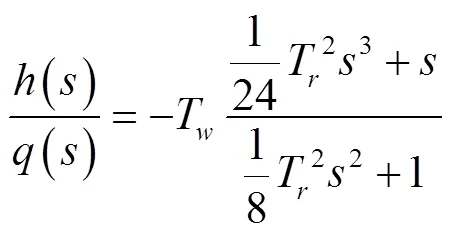
式中(0)/Q=∆Q/Q(0)/H=∆H/H。0和0分别为扰动前的流量(m3/s)和水头(m)；T为水流加速时间，s；T为水击波相长，s；T=L/c，为引水系统长度，m，为水击波波速，m/s；为拉普拉斯算子。如果不考虑水流及管道的弹性，令T=0，可得到刚性水击引水系统传递函数()=-Ts。

水轮机数学模型：采用在稳态工况点局部线性化的方法，用水轮机的传递系数来表述的水轮机稳态特性如下式所示

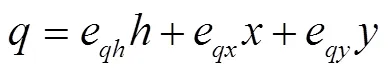
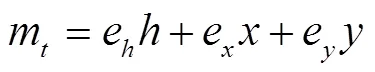
式中(0)00，0和分别为扰动前后水轮机的转速，r/min。由于机组负荷调节过程中并大网运行，此时认为转速无变化，即0；(0)00，0和分别为扰动前后的水轮机开度；m=(M-M0)/M0=∆M/M0，M和M0分别为扰动前后作用于水轮机的水力力矩；e、e、e、e、e、e为水轮机6个传递系数。

对于水轮机调速器功率控制模式，在并网后一般采用PI调节[7]，可以得到其传递函数为

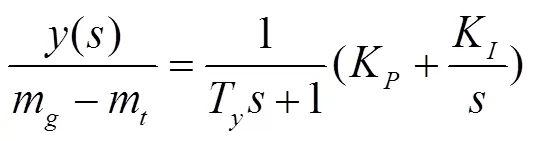
式中m为水轮机阻力力矩变化相对值，其值可以反映水轮机有功功率变化的大小。

根据以上各子系统数学模型可推导得出水电机组负荷调节过渡过程总传递函数为

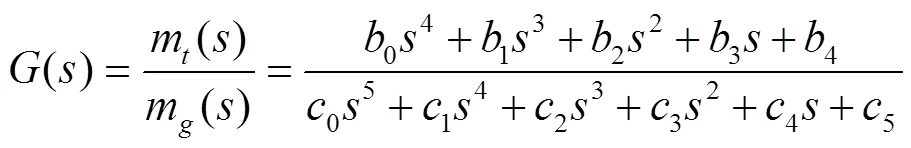
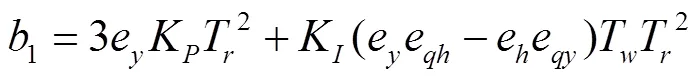
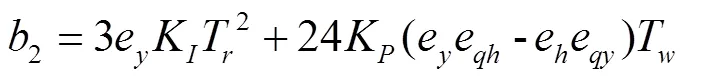
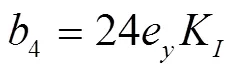
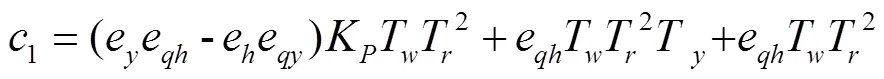
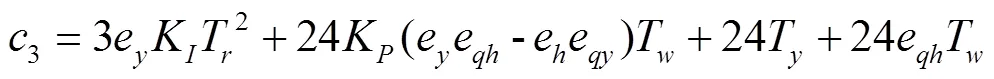
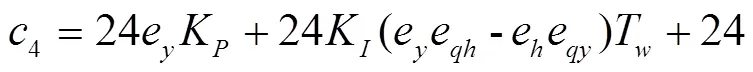
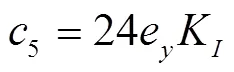
1.2 稳定性数值分析

根据常微分方程稳定理论，当式（5）所示系统的特征方程的各系数只有满足以下Routh-Hurwitz稳定条件

1）各项系数大于0，即001020304050；

2）各系数组成的Hurwitz行列式大于0，即212-030，4(12-03)(34-25)-(14-05)2，系统才是稳定的。

取理想水轮机参数e=1.0，e=1.5，e=1.0，e=0.5，T值可根据实际水电站设计图纸计算得到，本次计算取5.268 s，T值可根据实测辨识获得[27]，本次计算取0.04 s，取水击波波速分别为1 400、1 000、800 m/s，同时采用刚性水击模型，得到以调速器参数K、K为变量的稳定域如图2所示，图中各曲线为刚性水击以及不同水击波速下的稳定域边界，图中位于曲线左下部为稳定区域，反之则为不稳定区域。

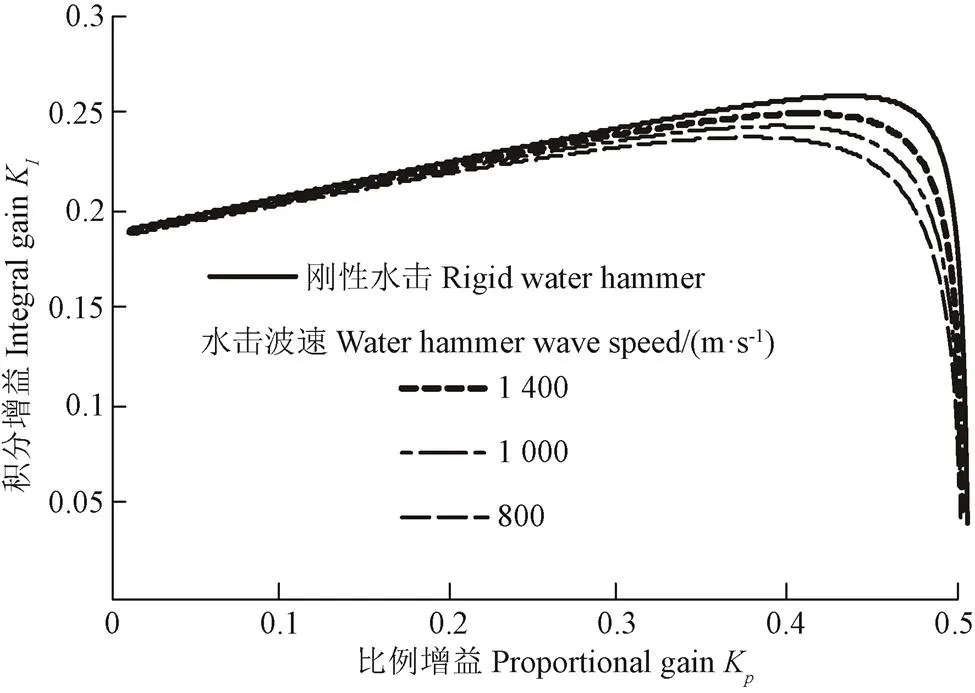
图2 不同波速计算结果

由图2可知，随着波速的变化稳定边界线的两端几乎无变化，边界线的中间段随着波速的增大，稳定域增大，且接近刚性水击稳定边界线。

由于弹性水击下的系统为5阶系统，很难从理论上推导稳定域，根据文献[28]的研究成果，对于水轮机控制系统，由于其波动周期为数秒钟，可用刚性水击模型，分析图2可知弹性水击与刚性水击的临界稳定边界线差别不大。因此可以采用刚性水击模型对稳定域进行理论分析，其具有一定的指导意义。

2 基于刚性水击的稳定域理论推导

基于刚性水击从理论上推导水电站调速器功率模式下负荷调节过渡过程稳定域，得出合理的调速器参数K、K取值范围。

令式（5）各项系数中的T=0，则得到刚性水击下系统总的传递函数。该系统的特征方程为

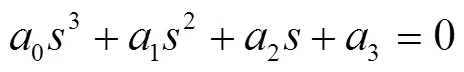
式中0=24eTT；1=−24eeTK+24T+24eT；2=24eK−24eeKT+24；3=24eK，其中=ee/e−e，为水轮机综合特性系数[24]。

根据Routh-Hurwitz稳定条件可知0>0，1>02>0，3>0及Hurwitz行列式2>0时系统才是稳定的。显然0>0及3>0是恒成立的，只需分析1>02>0及2>0。

在进行稳定域推导之前，首先分析特征方程系数中的水轮机传递系数e、e和的正负值。e为水轮机力矩对导叶开度的偏导数，其值总大于0；e为水轮机流量对水头的偏导数，其值也是恒大于0的；为水轮机综合特性系数，由文献[29]可知，=－()反映的是出力不变、转速不变的条件下，水轮机流量相对变化率与水头相对变化率的关系，由于与是成反比的，因此恒大于0。

由于e、e和恒大于0，故可根据1>02>0及2=12－03>0，得出

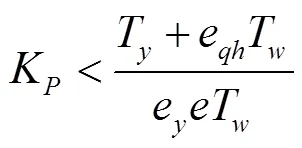
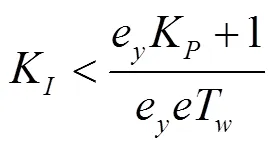
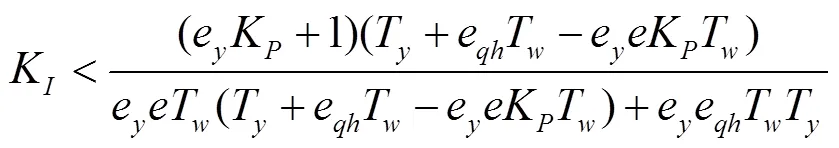
T=0.1 s、T=3.0 s时式（7）～式（9）取等号时对应的曲线，可知式（9）为双曲线，式（8）为该双曲线的一条渐近线，式（7）为双曲线下半支与轴的交点，即当K=0时，根据式（9）可得出K=(T+eT)/eeT，此式刚好为式（7）取等号的情况。由图3易得出，稳定区域即为双曲线下半支包含的区域。

由以上分析可知，基于刚性水击满足水电站调速器功率模式下负荷调节过渡过程稳定性的条件为

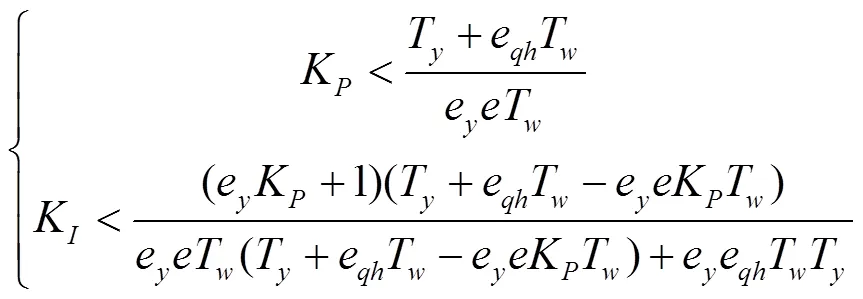
3 本文稳定域计算公式的验证

根据本文推导的稳定域判别式（10），取理想水轮机参数e=1.0，e=1.5，e=1.0，e=0.5，及T=0.4s、T=2.0s，计算得出水电站功率调节模式下负荷调节过渡过程稳定域边界线如图4a所示。由动力系统稳定域理论可知，当参数取值位于稳定域边界上则系统受小扰动后波动是等幅振荡的；当参数取值位于稳定域边界外（图4a中稳定边界线右上方）则系统受小扰动后波动是发散的；当参数取值位于稳定域边界内（图4a中稳定边界线左下方）则系统受小扰动后波动是稳定收敛的。

为验证本文稳定域的计算公式，分别在稳定域边界上任取一点1(K=0.4、K=0.526)，稳定域边界线外任取一点2(K=0.4、K=0.6)，稳定域边界上任取一点3(K=0.4、K=0.3)，进行m向上阶跃0.2时的负荷调节过渡过程模拟，计算结果如图4b所示。

注：特征点1位于稳定域边界，特征点2位于稳定域边界右上方（边界外），特征点3位于稳定域边界左下方（边界内）。

由图4可知，稳定边界线上的计算结果是等幅振荡的，在边界外的点（即不稳定区域）计算结果是发散的，在边界内的点（即稳定区域）是收敛的，在18.6 s时稳定在目标值。由此亦可佐证本文推导的稳定条件的正确性。

4 稳定域影响因素分析

4.1 Tw值及Ty值对系统稳定域的影响

根据式（10），取理想水轮机参数，分析T及T对系统稳定域的影响，如图5所示。图5a以T为参变量，T取固定值0.4 s，图5b以T为参变量，T取固定值2.0 s。

分析图5a可知，随着T值的增大，稳定域面积不断缩小，不利于系统的稳定；图5b中可用对角线将稳定域边界线分为上、下半支，随着T值的增大，边界线上半支下移，对稳定性不利，但下降幅度不大；边界线下半支右移，对稳定性有利，且变化幅度较大；由此可知当T值变大时，K可取大值，而K则应取小值。总体来看，随着T值的增大，稳定域面积增大，有利于系统的稳定。

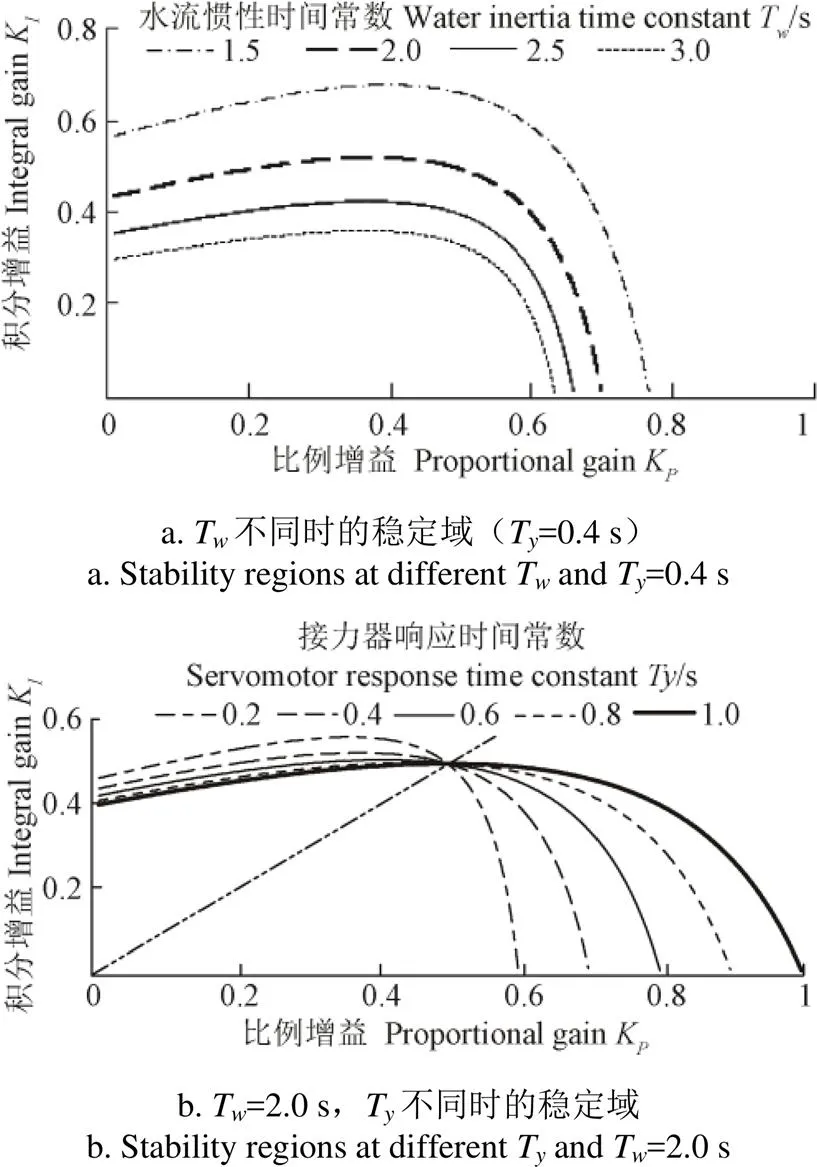
图5 不同Tw及Ty下的稳定域

4.2 水轮机运行工况对系统稳定域的影响

本文以某实际水电站为例，分析水轮机运行工作范围内不同工况点下的稳定域。某单管单机水电站基本参数为：水轮机额定出力44.92 MW，额定水头42.40 m，最小水头38.00 m，最大水头54.99 m，额定转速136.4 r/min，额定流量118.04 m3/s，T值为5.268 s，转轮直径3.85 m，转轮型号A551-35.2，水轮机特性曲线如图6所示。

4.2.1 不同水头下稳定域的变化规律

取T为0.4 s，导叶相对开度66.12%（绝对开度18.51 mm，如图6绿线所示），分析最小水头38.00 m、额定水头42.40、45.00、49.00、52.00 m，最大水头54.99 m下稳定域的变化规律，此6种水头对应的工况点如图6中△所示，传递系数如表1所示。各工况点下计算的稳定域如图7所示。

注：图中标记△的为相同导叶开度（66.12%）下，不同水头下的工况点；图中标记○的为在3个特征水头下（38.00、42.40、49.00 m），相同水头不同导叶开度下的工况点。

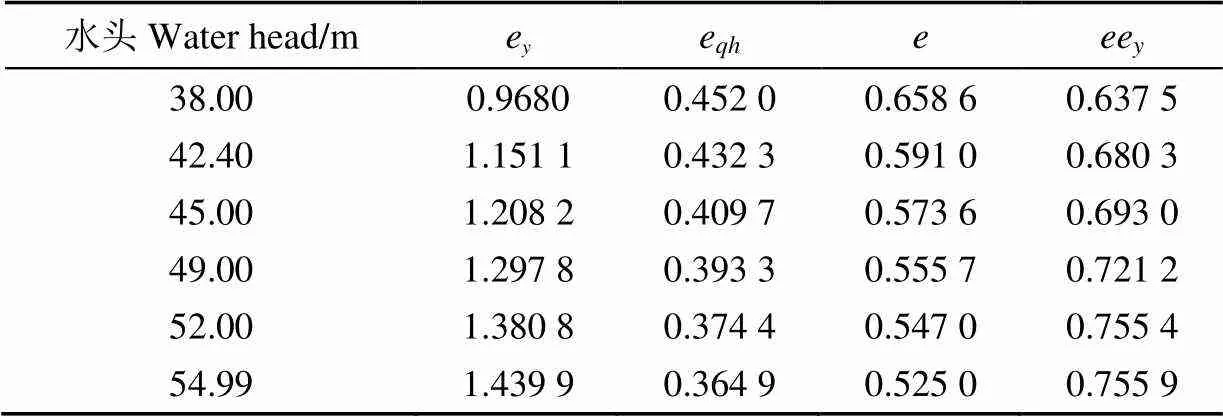
表1 不同水头下水轮机传递系数（开度为66.12%）

分析图7可知，当开度相同时，随着水头的增大，稳定域面积越小，稳定性越差。其主要原因为随着水头的增大，e逐渐减小，ee逐渐增大，因此K（如式（10）可知）逐渐减小，稳定域减小。由于最大水头时ee最大，因此其稳定性最差。

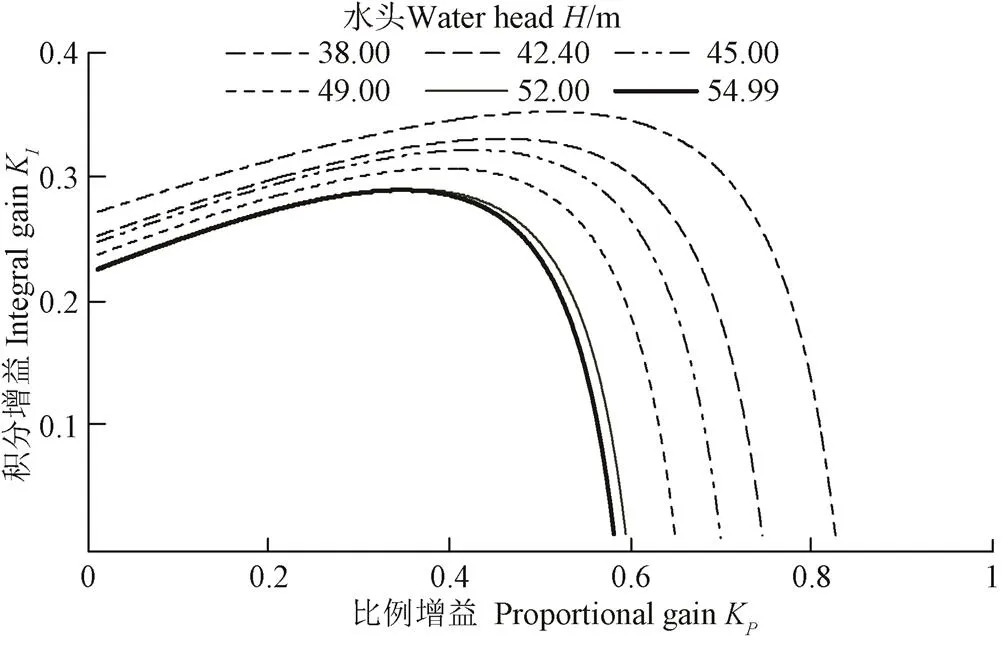
图7 相同开度不同水头下的稳定域

4.2.2 不同开度下稳定域的变化规律

取T为0.4 s，分析最小水头38.00 m、额定水头42.4和49.00 m水头下，不同开度时稳定域的变化规律。3种水头下，各开度对应的工况点如图6中○点所示，传递系数如表2所示。各工况点下计算的稳定域如图8、9所示。

表2 3种水头下各开度水轮机传递系数

分析图8可知，3种水头下最小稳定域分别发生在导叶开度为73.36%、81.15%及73.04%的工况点处，对比表 2可知，这3种开度对应的工况点的ee值分别是相同水头下的最大值。因此可以得出，相同水头下稳定域最不利的工况点为ee值最大处。

图8 不同水头下不同导叶开度下的稳定域

4.2.3 最不利工况分析

由4.2.1及4.2.2两小节的分析来看，ee值最大处为稳定性最不利的工况点。根据图6所示的综合特性曲线，计算得出任一工况点的ee值，如图9所示，图中红色线为该电站水轮机运行工作范围边界线。

对比图6和图9可知，在高效率区附近ee值较大，在高效率区下方出现最大值，因此高效率区下方的高水头工况为稳定性最不利工况。在实际工程中可以根据水轮机的工作范围与高效区的相对位置，来初步确定最不利工况，如本水电站水轮机工作范围包含高效区，因此在大于额定水头小于最大水头满负荷运行时的工况为最不利工况。

图9 A551-35.2水轮机任一工况点的eye值分布图

5 结 论

本文对水轮机调速器功率模式下负荷调节过渡过程的稳定性进行了分析，得出了以调速器参数为变量的机组运行稳定域，并推导出了满足调速器功率模式下负荷调节过渡过程稳定性的判别式，分析了水流惯性、接力器响应特性以及水轮机特性对稳定域的影响，得出以下主要结论：

1）通过对不同水锤波速下机组稳定域的对比可知，水锤波的波速对调速器功率模式稳定域的影响有限，弹性水锤模型和刚性水锤模型下得到的稳定域差别不大。

2）水流惯性时间常数T值对稳定域的影响较大。随着T值的增大，稳定域面积不断缩小，不利于系统的稳定。

3）调速器反应时间常数T值对稳定域的影响较大。随着T值的增大，稳定边界K略有减小但K有明显的增加。总体来看，随着T值的增大，稳定域面积增大，有利于系统的稳定。当T值减小时，为保证功率调节过程的稳定，调速器K值应减小。

4）水轮机运行工况对系统稳定域有较大影响。本文通过某一水电站工程实例对“相同开度，不同水头”及“相同水头，不同开度”下的工况点进行稳定域计算，得出随着水头的增大，水轮机综合特性系数与水轮机传递系数e乘积值（即ee）逐渐增大，稳定域面积逐渐减小，稳定性变差；同时得出稳定域大小与ee值密切相关，ee值越大，系统稳定域越小，稳定性越差。根据水轮机综合特性曲线计算得出任一点ee值，发现在高效率区附近ee值较大，在高效区下方出现最大值。因此由水轮机的工作范围与高效区的相对位置，可初步确定负荷调节稳定性的最不利工况点，如本文实例中水轮机工作范围包含高效区，因此在大于额定水头小于最大水头满负荷运行时的工况为最不利工况。

[1] 程春田，励刚，程雄，等. 大规模特高压直流水电消纳问题及应用实践[J]. 中国电机工程学报，2015，35(3)：549－560. Cheng Chuntian, Li Gang, Cheng Xiong, et al. Large-scale ultra High voltage direct current hydropower absorption and its experiences[J]. Proceedings of the CSEE, 2015, 35(3): 549－560. (in Chinese with English abstract)

[2] 易跃春. “十三五”我国水电及新能源发展路径[J]. 中国电力企业管理，2017，4(7)：27－30. Yi Yuechun. “Thirteenth Five-Year Plan” development path of hydropower and new energy in China[J]. China Power Enterprise Management, 2017, 4(7): 27－30. (in Chinese with English abstract)

[3] 路晓敏，陈磊，陈亦平，闵勇，侯君，刘映尚. 电力系统一次调频过程的超低频振荡分析[J]. 电力系统自动化，2017，41(16)：64－70. Lu Xiaomin, Chen Lei, Chen Yiping, et al. Ultra-low-frequency oscillation of power system primary frequency regulation[J]. Automation of Electric Power Systems, 2017, 41(16): 64－70. (in Chinese with English abstract)

[4] 周益华，竺炜. 水轮机及其调速系统对电力系统低频振荡的影响分析[J]. 中国水能及电气化，2012(4)：13－18. Zhou Yihua, Zhu Wei. The study of low-frequency oscillations of hydro-turbine speed control system in power system[J]. China Water Power & Electrification, 2012(4): 13－18. (in Chinese with English abstract)

[5] 黄海军，王秋晨，刘照友. 论AGC功能在大型水电机组中应用的优化策略[J]. 云南水力发电，2018，34(3)：119－123. Huang Haijun, Wang Qiuchen, Liu Zhaoyou. Discussion on optimization tactics of application of the AGC function to large hydropower plant power generation units[J]. Yunnan Water Power, 2018, 34(3): 119－123. (in Chinese with English abstract)

[6] 乔亮亮，李晨坤，付亮，等. 某250MW水电机组振动区划分及AGC避振方法应用[J]. 水电能源科学，2018，36(9)：152－154. Qiao Langliang, Li Chenkun, Fu Liang, et al. Vibration zone division of a 250 MW hydropower unit and application of AGC vibration avoidance method[J]. Water Resources and Power, 2018, 36(9): 152－154.(in Chinese with English abstract)

[7] 魏守平. 水轮机调节[M]. 武汉：华中科技大学出版社，2009：40－42.

[8] Wang Guoteng, Xu Zheng, Guo Xiangyang, et al. Mechanism analysis and suppression method of ultra-low-frequency oscillations caused by hydropower units[J]. Electrical Power and Energy Systems, 2018, 103: 102－114.

[9] Yang Weijia, Per Norrlund, Johan Bladh, et al. Hydraulic damping mechanism of low frequency oscillations in power systems: Quantitative analysis using a nonlinear model of hydropower plants[J]. Applied Energy, 2018, 212: 1138－1152.

[10] 黄伟，段荣华，江崇熙，等. 多机系统超低频振荡稳定分析与调速器参数优化[J]. 电力系统自动化，2018，42(21)：185－193. Huang Wei, Duan Ronghua, Jiang Chongxi, et al. Stability analysis of ultra-low frequency oscillation and governor paramaeter optimization for muli-machine system[J]. Automation of Electric Power Systems, 2018, 42(21): 185－193. (in Chinese with English abstract)

[11] Mo Weike, Chen Yiping, Chen Haoyong, et al. Analysis and measures of ultra-low-frequency oscillations in a large-scale hydropower transmission system[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(3): 1077－1085.

[12] 徐敏，涂亮，柳勇军，等. 水电机组高占比电网频率振荡问题分析[J]. 广东电力，2017，30(7)：46－52. Xu Min, Tu Liang, Liu Yongjun, et al. Analysis on frequency oscillation of power grid with high-proportion hydro-electric generating set[J]. Guangdong Electric Power, 2017, 30(7): 46－52. (in Chinese with English abstract)

[13] 高海翔，伍双喜，苗璐，等. 发电机组引发电网功率振荡原因及其抑制措施研究综述[J]. 电网分析与研究，2018，46(7)：49－55，66. Gao Haixiang, Wu Shuangxi, Miao Lu, et al. Overview of reasons for generator-induced power oscillations & its suppression measures[J]. Grid Analysis & Study, 2018, 46(7): 49－55, 66. (in Chinese with English abstract)

[14] 伍双喜，徐衍会，张莎，等. 机组引发低频振荡的传播特性分析及定位研究[J]. 电网技术，2018，42(6)：1917－1921. Wu Shuangxi, Xu Yanhui, Zhang Sha, et al. Research on propagation characteristics and locating method of low frequency oscillations induced by turbine generator unit[J]. Power System Technology, 2018, 42(6): 1917－1921. (in Chinese with English abstract)

[15] 关欣. 大惯性比率水电机组对现代电力系统稳定性的影响[D].西安：西安理工大学， 2018. Guan Xin. The Influence of Large Inertia Ratio Hydro-Power Unit on the Stability of Modern Electric Systerm[D]. Xi’an: Xi’an University of Technology, 2018. (in Chinese with English abstract)

[16] Sun Zhenglong, Cai Guowei, Yang Deyou, et al. Application of power system energy structures to track dominated oscillation paths and generator damping contribution during low-frequency oscillations[J]. International Journal of Electrical Power & Energy Systems, 2019, 104: 52－68.

[17] Wang Guoteng, Xu Zheng, Guo Xiangyang, et al. Mechanism analysis and suppression method of ultra-low-frequency oscillations caused by hydropower units[J]. International Journal of Electrical Power & Energy Systems, 2018, 103: 102－114.

[18] 张建新，刘春晓，陈亦平，等. 异步联网方式下云南电网超低频振荡的抑制措施与试验[J]. 南方电网技术，2016，10(7)：35－39. Zhang Jianxin, Liu Chunxiao, Chen Yiping, et al. Countermeasures and experiments on ultra-low frequency oscillation of yunnan power grid in asynchronous interconnection mode[J]. Southern Power System Technology, 2016, 10(7): 35－39. (in Chinese with English abstract)

[19] 魏守平，王雅军，罗萍. 数字式电液调速器的功率调节[J]. 水电自动化与大坝监测，2003，27(4)：20－22. Wei Shouping, Wang Yajun, Luo Ping. Power adjustment of digital electric-hydraulic governor[J]. Hydropower Automation and Dam Monitoring, 2003, 27(4): 20－22. (in Chinese with English abstract)

[20] 陈艳，李学礼. 基于自适应 PID 控制的水电站有功功率调节[J]. 大电机技术，2016(1)：62－64. Chen Yan, Li Xueli. Active power regulation based on self adapting PID controller[J]. Large Electric Machine and Hydraulic Turbine, 2016(1): 62－64. (in Chinese with English abstract)

[21] 魏加富，邹桂丽，孟佐宏，等. 基于三段速度调节的水电机组功率调节模式探讨[J]. 水电自动化与大坝监测，2014，38(3)：3－4，29. Wei Jiafu, Zou Guili, Meng Zuohong, et al. Power regulation mode study nased on three-stage speed regulation of hydropower unit[J]. Hydropower Automation and Dam Monitoring, 2014, 38(3): 3－4, 29. (in Chinese with English abstract)

[22] 付亮. 带变顶高尾水洞水电机组调速器功率模式优化研究[J].水力发电学报，2018，37(3)：88－95. Fu Liang. Optimization of governor power mode for hydro-turbine units with slope ceiling tail tunnels[J]. Journal of Hydroelectric Engineering, 2018, 37(3): 88－95. (in Chinese with English abstract)

[23] 刘国富，王晓瑜，金玉成. 水轮机调速器改进型控制结构结合增量式PID算法的功率调节及一次调频的实现[J]. 大电机技术，2016(4)：61－64. Liu Guofu, Wang Xiaoyu, Jin Yuchen. The realization of improved power regulation control structure and the frequency primary regulation for hydraulic turbine governor[J]. Large Electric Machine and Hydraulic Turbine, 2016(4): 61－64. (in Chinese with English abstract)

[24] 高晓光，唐戢群. 构皮滩水电机组功率模式下的一次调频功能试验研究[J]. 水电站机电技术，2015，38(9)：25－28. Gao Xiaoguang, Tang Jiqun. Study on pfr function test of Goupitan hydropower unit in power mode[J]. Mechanical & Electrical Technique of Hydropower Station, 2015, 38(9): 25－28. (in Chinese with English abstract)

[25] 尹利群，王雄，付亮，等. 水电机组有功波动分析及处理[J].湖南电力，2017，37(5)：51－59. Ying Liqun, Wang Xiong, Fu Liang, et al. Analysis and treatment on active power fluction of hydro generator[J]. Hunan Electric Power, 2017, 37(5): 51－59. (in Chinese with English abstract)

[26] 纪可可，徐亮，汪志华. 二滩水电站3号机组低频振荡原因分析[J]. 人民长江，2016，47(21)：103－105. Ji Keke, Xu Liang, Wang Zhihua. Cause analysis of low frequency oscillation of unit 3 in Ertan Hydropower Station[J]. Yangtze River, 2016, 47(21): 103－105. (in Chinese with English abstract)

[27] 国家能源局.同步发电机原动机及其调节系统参数实测与建模导则：DL/T 1235—2013 [S]. 北京：中国电力出版社，2013.

[28] 沈祖诒. 水轮机调节系统分析[M]. 北京: 水利电力出版社，1991.

[29] 杨建东，赖旭，陈鉴治. 水轮机特性对调压室稳定断面积的影响[J]. 水利学报，1998，29(2)：7－11. Yang Jiandong, Lai Xu, Chen Jianzhi. The effect turbine characteristic on stable sectional area of surge tank[J]. Journal of Hydraulic Engineering, 1998, 29(2): 7－11. (in Chinese with English abstract)

Stability of load regulation transition process of hydro turbine governor in power regulation mode

Bao Haiyan1, Long Liting1, Fu Liang2, Wei Jiafu2

(1.,,410114,;2.,410007,)

Whether the load regulation transition process of the hydropower unit can be stably carried out will have an important impact on the safe operation of the power grid and the coordination of the source network as it is the backbone power supply for peak and frequency modulation in the power system,. During the load regulation transition process, the governor power mode automatically completes the power closed-loop regulation by the governor, and quickly responds to the load adjustment command issued by the AGC, which responses fast and realizes the coordinated control of the primary frequency modulation and the AGC. Due to the combination of water hammer effect, the nonlinearity of the turbine and the time-varying parameters, the stability characteristics of load regulation transition process of hydropower units become more complicated than imagined. At present, the research on governor power mode mostly focuses on control logic, experimental simulation and control parameters optimization and rarely involves the stability problem of load regulation. Yet there are actually more than one hydropower plants that have experienced instability during operation. The problem of instability in the power mode leads to power oscillation, endangering the security of the grid and the coordination of the source network. In this paper, the method of theoretical analysis and numerical simulation is used to deeply analyze the stability of the transition process of load regulation under the governor power mode of hydraulic turbine, therefore the stability region of unit operation with the governor parameters as variables is obtained and the discriminant for the stability of load regulation transition process in the power mode of governor is deduced. Through this discriminant, the stable condition of load regulation transition process can be obtained quickly, and the parameter setting of governor in power mode can be effectively guided to ensure the stable operation of hydropower unit. The influence of water flow inertiaT, servo response characteristicTand turbine characteristics on the stability domain are analyzed. The results show that the value ofThas a great influence on the stability region. As the value ofTincreases, the area of the stable region decreases, which is not conducive to the stability of the system. With the increase of T’s value, the area of the stability region increases, which is conducive to the stability of the system. WhenT’s value decreases, the governor parameterKshould be reduced in order to ensure the stability of the power regulation process. The study also indicates that the operating condition of water turbine has a great impact on the system's stability region. The size of the stability region is closely related to the product value of the comprehensive characteristic coefficient of water turbineand the transfer coefficient of water turbinee. The larger the product value, the smaller the system's stability region. Based on the research results of this paper, a detailed analysis of a case of hydropower unit is carried out. According to the comprehensive characteristic curve of the turbine, the most unfavorable working condition of power regulation stability can be accurately found. The research results of this paper can effectively guide the safe operation of hydropower units, which is of great significance to the safety of the power grid and the coordination of the source network.

hydropower station; hydro turbine; power mode; load regulation; stability; governor parameters

2018-12-21

2019-08-27

国家自然科学基金资助项目（51309033）

鲍海艳，副教授，博士，从事水电站过渡过程的研究。Email：83369537@qq.com

10.11975/j.issn.1002-6819.2019.17.007

TK43

A

1002-6819(2019)-17-0050-08

鲍海艳，龙丽婷，付 亮，魏加富. 水轮机调速器功率调节模式下负荷调节过渡过程稳定性研究[J]. 农业工程学报，2019，35(17)：50－57. doi：10.11975/j.issn.1002-6819.2019.17.007 http://www.tcsae.org

Bao Haiyan, Long Liting, Fu Liang, Wei Jiafu. Stability of load regulation transition process of hydro turbine governor in power regulation mode[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(17): 50－57. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.17.007 http://www.tcsae.org