DNTF凝固过程显微疏松的模拟计算和试验研究

2019-11-11刘瑞鹏贾宪振王永顺

火炸药学报 2019年5期

刘瑞鹏，贾宪振，王永顺

(西安近代化学研究所, 陕西西安 710065)

引言

DNTF是一种常用的熔铸载体炸药，其凝固特性会对炸药装药结构产生显著影响。许多研究者对DNTF的宏观凝固特性进行了分析。王亲会等[1]对DNTF的能量特性和熔铸性质进行了研究，认为DNTF熔融态时的黏度和流动性适合熔铸炸药工艺；蒋秋黎等[2]获得了TNAZ/DNTF双元载体的组分—温度相图，并研究了低共熔物的热安定性等熔铸性能；刘瑞鹏等[3]对TNT、DNAN及DNTF等3种载体宏观缩松结果进行了数值模拟，并分析了它们的宏观凝固机理；罗一鸣等[4]分析了TNT、DNTF的凝固行为，认为DNTF具有体积凝固的机理。由以上研究可知，DNTF具有体积收缩小、相变潜热少、比热容和导热系数低等材料特性。对于DNTF凝固过程宏观规律的认识较为深刻。

除了宏观缩孔以外，DNTF凝固过程中还会形成许多显微疏松缺陷。这种缺陷导致炸药成型密度低、安定性差，对装药结构产生不利影响。而显微疏松明显不同于宏观缩孔。目前关于显微疏松的研究多集中在金属材料领域[5-11]，金属熔体在凝固过程中形成的凝固缺陷可分为宏观缩孔、缩管及显微疏松等3种形式，但关于DNTF显微疏松方面的研究报道较少。

本研究采用数值模拟与试验验证的方法对DNTF凝固过程显微疏松进行了探索研究，对温度曲线进行了拟合分析，构建了DNTF显微疏松的计算模型，为深入理解DNTF显微疏松的形成规律提供参考。

1 计算模型构建

DNTF体积凝固的特性容易导致整体凝固而产生缺陷。凝固过程还包含枝晶结构的形成过程[12]。液固密度差使DNTF凝固时产生体积收缩。枝晶结构阻碍了液相的补缩作用，导致缺陷产生。同时液相中析出的气体也会形核而产生疏松。当析出气体压力与补缩阻力之和超过环境压力与液相静水压之和时[5,10]，就会在凝固过程中产生显微疏松。显微疏松的形成与质量守恒、动量守恒、热传导以及气体含量守恒等4个方面相关。

1.1 质量守恒

建立质量守恒方程时进行了3点假设：固相是静止的；固相是无变形的；忽略气体质量。质量守恒方程如式(1)、(2)所示：

(1)

gs+gl+gp=1

(2)

式中：ρs为固相密度，ρl为液相密度；gsgl和gp分别为固相、液相和气相的体积分数；v为枝晶骨架间液相的流动速度。

1.2 动量守恒

以达西定律描述糊状区枝晶结构间液相的流动，如式(3)所示：

(3)

式中：Pd为液相补缩阻力；Pl为局部压力；g为重力；K为枝晶结构的渗透率；μ为液相黏度。

其中渗透率K采用科泽尼-卡尔曼方程进行计算，如式(4)所示。其中λ2为二次枝晶臂间距。

(4)

1.3 热传导

假定DNTF是各向同性的，以傅里叶热传导定律描述凝固时的温度变化，如式(5)所示：

(5)

式中：T为温度；t为时间；cp为比热容；λ为导热系数；Q为相变潜热。采用温度补偿法对相变潜热进行处理，即将每个时刻释放的相变潜热折算成可补偿的温度值。

1.4 气体含量守恒

一般情况下，DNTF熔体中会混入少量气体杂质。考虑气体在固相和液相中的溶解，采用杠杆定律对气体分配过程进行描述，如式(6)所示：

(6)

式中：[c]0为DNTF熔体中混入的气体浓度；[c]s和[c]l分别为固相和液相中的气体浓度；α为气体转换系数；Pp为气体压力。

2 模拟计算

在理论分析基础上，首先采用ProCAST软件中的热传导模块对DNTF凝固过程温度变化进行模拟计算，之后在此结果前提下继续使用高级缩松模块对凝固过程显微疏松进行数值模拟。

计算模型由DNTF熔体和铜质模具两部分组成，如图1所示。其中DNTF熔体尺寸为Ф60mm×120mm；铜质模具的厚度为10mm。四面体计算网格总数为228803。

铜质模具使用软件自带的材料数据。DNTF材料参数如表1所示。表中列出的数据取自试验测试结果，其中导热系数、比热容在模拟计算时假定为常数。

图1 计算模型及网格划分Fig.1 Computational model and mesh

表1 DNTF材料参数

注：ρs为固相密度；ρl为液相密度；λ为导热系数；cp为比热容；Tl为液相线温度；Ts为固相线温度；Q为相变潜热。

DNTF熔体的初始温度为110℃，浇注速度为1.5m/s，铜质模具的初始温度为25℃。计算最大时间步长为1s，计算总步数为5000步，计算停止温度为30℃。首先使用热传导模块对DNTF凝固过程温度结果进行求解计算。

显微疏松的模拟计算需要以温度计算结果为前提。为此，需要根据用户手册手工编辑参数文件，对DNTF凝固过程的二次枝晶臂间距、气体含量、形核半径及网格间距等参数进行定义。其中二次枝晶臂间距是对DNTF凝固样品微观形貌扫描电镜结果进行分析而获得的计算参数。气体含量及形核半径计算参数参考了文献[9-11]的研究结果，并结合DNTF熔体性质经反复修正计算而得到的。网格间距是对计算误差和计算耗时进行综合衡量而确定的计算参数。之后再使用高级缩松模块(Advanced Porosity Module, APM)，在温度模拟计算结果的基础上，叠加使用有限差分方法，对DNTF显微疏松进行迭代计算。求解完成后使用后处理模块对计算结果进行处理。

3 试验验证

试验验证模型如图2所示。试验中使用的DNTF原料由甘肃银光化学工业集团有限公司生产，经西安近代化学研究所精制。模具为铜质，外观尺寸与计算模型相一致。

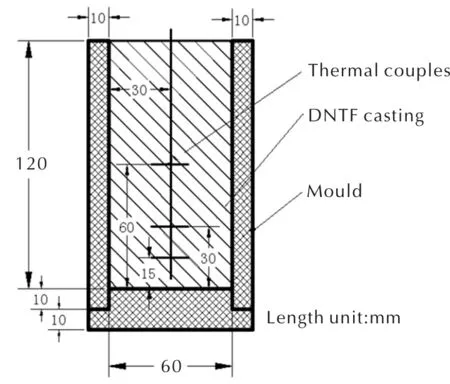
图2 试验方案示意图Fig.2 Schematic diagram of the experiment process

试验时以过饱和蒸汽为热源，在熔化锅中将DNTF完全熔化成液相，以1.5m/s的速度浇注到上述模具中。采用测温热电偶记录凝固时不同测点处的温度变化结果，试验共设置3个测点，距模具底面中心的垂直距离h分别为15、30和60mm。当DNTF液相物料完全凝固冷却后，去除外部铜质模具，采用450kV工业CT进行显微疏松检测。

4 结果与分析

4.1 DNTF凝固过程温度变化

图3为DNTF凝固过程中距模具底面中心的垂直距离(h)分别为15、30和60mm测点处温度试验结果、计算结果及拟合结果对比图。采用四参数Logistic模型对试验结果进行拟合，Logistic模型如式(7)所示，其中A1、A2、x0和p为待拟合参数。拟合结果如表2所示。

y=A2+(A1-A2)/(1+(x/x0)p)

(7)

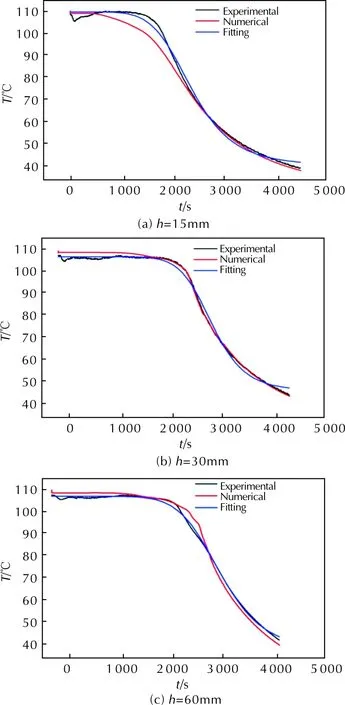
图3 不同测温点处DNTF凝固过程温度试验结果、计算结果及拟合结果对比图Fig.3 Comparison of experimental, numerical and fitting results for temperature during DNTF solidification process at different positions

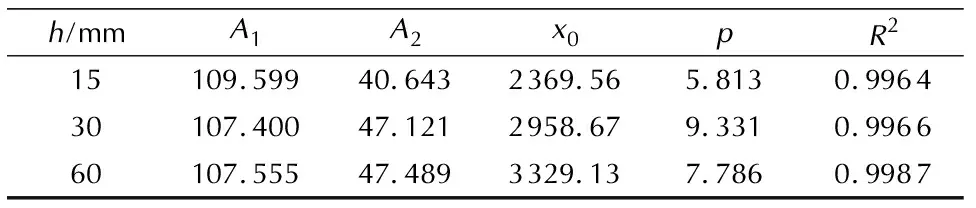
h/mmA1A2x0pR215109.59940.6432369.565.8130.996430107.40047.1212958.679.3310.996660107.55547.4893329.137.7860.9987

由图3可知，DNTF凝固过程温度曲线可分为平衡阶段和降低阶段。平衡阶段体现的是凝固点温度附近液固两相共存的过程。降低阶段反映的是液相消失后由于传热而导致温度逐渐降低的过程。凝固过程中液固界面的迁移规律是由四周到中心，因此各个位置处两个温度阶段的持续时间有所不同。15mm测点在最下部，液相最快消失，因而平衡阶段最短；30mm测点处次之；而60mm测点处的平衡阶段最长。

3个测温点处的温度计算结果与试验结果相符。15mm测点处平衡阶段的计算结果偏低，而降低阶段的计算结果与试验结果一致，平均误差约为7.5%。30mm测点处平衡阶段及降低阶段计算结果与试验结果几乎一致，平均误差约为1.5%。60mm测点处温度拐点计算结果略滞后于试验结果，降低阶段计算结果稍低于试验结果，平均误差约为5.1%。15mm测点处平衡阶段计算精度较差的原因可能是：模具底部液固界面迁移速率大、液相消失快，相变潜热对温度补偿的折合时间过长而导致计算结果偏低。60mm测点处降低阶段计算结果略低的原因可能是：上部液相在周围环境冷却作用下首先凝固，导致热阻增大而使温度计算结果偏低。凝固过程温度变化容易受到热阻的影响。凝固初期主要为模具热阻，温度下降速率较小；随着凝固过程进行，温度下降速率逐渐增大；当达到某一限度时，液固界面热阻成为主要热阻，温度下降速率又逐渐减小。温度曲线变化规律符合Logistic模型。采用四参数Logistic模型进行拟合的准确度高，相关系数平均值约为0.997。

4.2 DNTF凝固过程显微疏松分析

图4为DNTF凝固过程显微疏松试验结果及计算结果对比图。

图4 DNTF凝固过程显微疏松试验及计算结果对比Fig.4 Comparison of experimental and numerical results for microporosity of DNTF solidification process

DNTF材料过冷度大，相变阶段短，体积凝固特征明显，使凝固后形成的药柱中存在许多气隙分布，导致装药结构整体致密程度较低。由图4可知，显微疏松结果大致可分为两个部分：药柱上部主要缺陷为大尺寸的封闭孔洞；药柱下部主要缺陷为微尺寸的空穴疏松。药柱上表面受到空气冷却作用，温度快速降低到凝固点以下而形成封闭表面。DNTF熔体受到重力作用向下流动补缩。由于上表面提前封闭，使得药柱上部无法补缩，因而容易形成较大孔洞缺陷。左图中上部空缺部分即为孔洞缺陷，相应的，右图中红色区域显示为宏观缺陷。药柱下部中显微疏松的分布位置更加随机，分布范围遍及整个区域。DNTF凝固过程中伴随着枝晶结构的形成过程。糊状区中粗大的枝晶结构阻碍了上部液相的补缩作用，并且DNTF凝固速率大，使得很多区域得不到充分补缩而产生空穴疏松。左图中弥散排布的浅色斑点即为显微疏松，而右图中药柱内部及四周无规散布的浅绿色节点代表的则是显微疏松。由此可见，DNTF凝固过程显微疏松计算结果与试验结果基本相符。

显微疏松的形成容易受到凝固条件、过冷度以及枝晶形态等因素的影响。DNTF凝固时的凝固速率高于其他常用熔铸载体炸药，糊状区域的补缩时间短，容易形成显微疏松。同时，DNTF高过冷度的材料特性使显微疏松形成的倾向性更大。DNTF枝晶形态也会对显微疏松的形成过程造成影响。二次枝晶臂间距的增大使糊状区与外界区域的连通性下降，将液相区分割成更细小的孤立封闭区域，关闭补缩通道，使补缩阻力明显增大，导致显微疏松更加分散。