一种改进的多目标正余弦优化算法
2019-11-11王万良李伟琨王宇乐
王万良,李伟琨,王宇乐,王 铮
(浙江工业大学 计算机学院视觉研究所,大数据重点实验室,杭州 310023)E-mail:lwk@zjut.edu.cn
1 引 言
随着技术的不断革新,工业生产的迅速发展,优化问题已逐渐成为现行科学与工程领域的研究热点.在这其中,元启发算法(Metaheuristic Algorithm,MA)扮演了极其重要的角色.其核心思想为通过每种算法的不同运算符,搜索并不断更新位置,使得找到最优解的概率增加.在过去的十几年间,元启发算法不断被开发与延伸,如遗传算法(Genetic Algorithm,GA)[1],差分进化算法(Differential Evolution,DE)[2],进化策略(Evolution Strategy,ES)[3],蚁群算法(Ant Colony Algorithm,ACO)[4],粒子群算法(Particle Swarm Algorithm)[5]等等.但随着设备的不断更新,信息的不断多元化发展,优化问题也从传统的单目标优化问题逐渐向复杂的多目标问题转化.区别于传统的单目标优化问题,多目标优化问题往往含有两个或三个相互矛盾的目标,且无法找到单一的最优方案来满足所有的目标,其最终结果为一组多个目标相互权衡后的结果集合,也被称为帕累托最优解集(Pareto Optimial Set,PS)[6]或非支配解集,非劣解集等.而这也使得多目标优化算法(Multi-Objective Evolutionary Algorithms,MOEAs) 获得了极大的关注.从早期的强化帕累托算法(Strength Pareto Evolutionary Algorithm,SPEA)[7],基于非支配排序的遗传算法2(Non-dominated Sorting Genetic Algorithm version 2,NSGA-II)[8],基于分解的多目标进化算法(Multi-Objective Evolutionary Algorithm based on Decomposition,MOEA/D)[9]到近些年来涌现出的许多新的多目标优化算法,如改进的多目标粒子群算法[10],多目标分解算法[11],基于偏好的多目标优化算法[12].正余弦算法(Sine-Cosine algorithm,SCA)[13]是近年来提出的一种非常有效的单目标优化算法,他通过采用正弦与余弦函数来有效的搜索空间,已经被应用到很多方面如手写体输入、图像检测、能源生产等[14].尽管如此.受限于其设计机理与筛选机制,这些算法仍难以满足现行的需求.鉴于此,本文提出一种改进的多目标正余弦优化算法(Improved Multi-Objective Sine Cosine Algorithm,IMSCA),该算法继承了原有SCA算法的优良性能,并引入了两种新的机制:反向学习机制与网格密度筛选机制.通过结合反向学习本文提出一种全新的初始化方法来来增强可行解的获得的几率,并通过引入网格坐标提出一种基于密度筛选的新机制来更新和保存非劣解集,最终使得算法在具有良好收敛能力的同时使获得的解具有良好的分布性,进而强化算法的性能.
本文其余章节安排如下,第二节介绍算法相关背景,第三节陈述算法设计与其具体机制.第四节通过将IMSCA与其他五个多目标优化算法在一系列标准测试函数上进行仿真实验来验证算法的良好性能,第五节通过将IMSCA与其他多目标算法在真实工程设计优化问题上进行对比分析,验证所提算法在解决实际问题中的性能.最后第六节总结全文.
2 背景知识
2.1 反向学习
反向学习(opposition-based learning,OBL)[15]的出现为算法的搜索提供了一种新的思路,通过反向学习策略,算法在搜索最优解的同时,还会对其相反方向的解进行评价,从而增大最优解的获得概率,进而提升算法收敛速度.其基础概念如下所示:

(1)
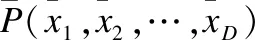
2.2 网格坐标
网格坐标是一种非常有效的空间划分机制,在这种机制中,一个网格被用作框架来确定个体在客观空间中的位置.它具有同时反映收敛性和多样性信息的内在属性.下面给出了网格的基础定义[16].
定义3.(网格边界)给定个体x在第dth个目标下的最小值和最大值为minfd(x)与maxfd(x).则其上边界与下边界为ud,ld,其具体公式如下:
(2)
(3)
其中h∈Z,h≥2为固定参数,表示在目标空间每一维度下的划分.
定义4.(网格坐标)给定个体x,第dth目标下的网格坐标可表示为:
(4)
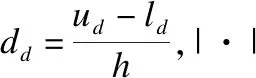
算法1.Improved Multi-Objective Sine Cosine Algorithm
Data:population siszN. external archive sizeN,objective numberM.
Result:optimal front.
begin

3 IMSCA算法框架
本文所提出的IMCSA算法伪代码如算法1所示.该算法由四个主要阶段组成.首先在初始化阶段,初始个体通过反向学习进行初始化.随后通过应用正余弦函数与反向学习获得子代解决方案.最后,通过在网格机制更新和保存外部解集,最终生成解决方案.在下面的段落中,将详细解释IMCSA中各个环节.
3.1 反向学习初始化
传统采用随机初始化的算法由于缺乏先验知识,大大降低了算法中较好区域的搜索几率.但利用OBL可以在没有先验知识的情况下,获得更适合的初始化候选解,从而提升探索到更好区域的概率.本文通过结合OBL,提出一种全新的方法来初始化IMSCA算法.其具体流程如下:
Step1.首先将初始种群PN分为两个部分,第一个部分PN1通过随机分布来产生.
Step2.第二个部分PN2通过2.1节中的反向学习方法来产生:
PN2=ai+bi-PN1
(5)
Step3.所产生的集合{PN1∪PN2}将作为初始种群NP带入算法的后续流程.
3.2 正余弦操作
正弦余弦算法(SCA)是一种基于种群的算法,在SCA中,为了高效探索并有效的更新位置,它使用了两种不同的数学表达式来更新每一代的解决方案.这些表达式如下[13]:
(6)
(7)

(8)
3.3 基于网格密度的筛选机制
为方便从子种群中筛选出优秀个体来构成新的种群,本文提出一种基于网格密度的新机制来辅助算法对较好的个体进行优先筛选,根据2.2节构建网格坐标后,每一个个体都有自己对应的网格坐标,首先采用全局网格排序进行筛选:
定义5.(全局网格排序)对于给定两个体x,y,个体x的全局网格排序(Global Grid Ranking,GGR)为:
(9)
其中M为目标个数,Gm(x),Gm(y)表示个体x,y在目标m上的网格坐标.GGR反映了个体的全局支配程度,换言之,一个个体其支配其他个体越多,其GGR值也就越大,则其被优先选择的几率也就越大.通过GGR的排序筛选,可以辅助算法快速筛选优秀个体,但个体仍可能存在GGR值相同的情况,针对此类情况,我们综合考虑其个体分布多样性提出一种基于网格密度排序(Grid Density Ranking,GDR)的新机制来进行进一步筛选最优个体,其定义如下:
定义6.(网格密度排序) 对于给定两个体x,y,个体x的网格密度排序为:
GDR(x)=find(GD(x,y) (10) (11) 全局网格密度排序GDR反映了个体周边的拥挤程度,换言之,一个个体与其他个体的密集程度越小,其GDR值也就越小,则其被优先选择的几率也就越大. 图1 网格密度排序Fig.1 Grid density ranking 如图1 所示为双目标最小化问题,个体p1,p2,p3,p4,p5,p6,p7的网格坐标分别为(3,5),(3,4),(2,4),(2,3),(1,3),(2,2),(3,2).从图中可以看出,个体p5,p6的GGR 值最大,支配的个体最多,但由于两个个体的GGR值均为13,此时我们采用GDR排序对其进行进一步筛选.对于个体p5,其与p6,p4,p3的GD 值分别为2,1,2,所以其GDR 值为1. 而对于个体p6,其与p5,p4,p7的GD 值分别为2,1,1,所以其GDR 值为2.p5的GDR 值更小,所以优先选择p5(从个体的密度来看,相比p6,p5周围拥挤度较低,多样性更好,则优先选择p5). 维护和更新非支配解集是算法中重要的一环.传统多目标优化算法大多采用建立一个外部档案来存储非支配解.当非支配解个数达到预定值时,需要对其进行删减,以提高算法的搜索效率,从而保持解的多样性.在这里,我们将外部存档的大小设置为N,与种群的大小相同,并使用3.3节中的GGR和GDR策略将前50% 的解决方案按升序存放到外部存档中.由于整个种群的分布在外部存档中发生了变化,因此需要重新计算网格排序来获得最优的帕累托前沿. 在本节,IMSCA算法将与5种优秀的多目标优化算法(NSGA-II,MOEA/D,AGE-II[17],IM-MOEA[18],NSLS[19])在一系列标准测试函数上进行对比,在这里,我们采用ZDT{1,2,3,4,6}、UF{4,5,6,7,8,9}与 DTLZ{1,2}测试函数[20]进行验证.此外,本文采用两个经典评价指标反转世代距离(Inverted Generational Distance,IGD)[16]与空间指标(Spacing,SP)[22]来对各个算法的结果进行评估,最后,为了客观的显示对比结果,本节还引入了秩序检验来对结果的差异性进行客观评估,从而验证所提算法的性能与表现. 本文引入了5种算法与IMSCA进行对比试验,其中各算法的参数设置如表1所示,为避免算法结果的偶然性,每个算法实验都独立运行30次进行统计. 表1 各算法参数设定Table 1 Parameters for each algorithms 采用IGD指标与SP指标的实验统计结果已经如表2,表3所示.表格中高亮部分的值为该行中的最优结果.为了方便对比,本节引入了秩序检验来评价各个算法所获得结果间的差异性,其统计结果以“w/t/l” 的形式被记录在各表格最后一行,其中w表示本文提出的IMSCA算法所获得结果优于该对比算法的结果;l表示本文提出的IMSCA所获得结果差于该对比算法;t表示该对比算法的结果与本文提出的IMSCA 所获得结果无明显的差异. 如表2所示,6个算法在IGD指标下的统计结果已经列在表中.从结果可以看出,IMSCA算法、NSGA-II算法,AGE-II与IM-MOEA算法包揽了所有13个测试函数在IGD指标下的最优值(最小值).对于ZDT系列测试函数,IMSCA 在ZDT1,ZDT2,ZDT3,ZFT4与ZDT6五个测试函数上都获得良好的表现,此外图2中第1、2、3行6个算法在ZDT4.ZDT6上所获得结果图也进一步验证了IMSCA算法的良好性能.对于UF系列测试函数,IMSCA在UF4,UF5,UF7与UF9上取得了最优值,NSGA-II包揽了UF6与UF8上的最优值.而MOEA/D算法、IM-MOEA算法、NSLS算法在UF测试函数上的表现较在ZDT上的表现略逊一筹,特别是在UF5测试函数上.对于UF6测试函数,尽管IMSCA的表现稍逊于NSGA-II与AGE-II算法,但仍优于其他算法的结果.对于UF7测试函数,IMSCA表现出了优良的性能,如图2中所示,IMSCA算法在UF7上的表现明显优于其他算法.此外,从图2第6行可以看出,IMSCA在UF9上的表现也较为出色.最后,对于DTLZ测试函数,IMSCA 与AGE-II两个算法分别取得了DTLZ1和DTLZ2上的最优值,但根据秩序检验结果,IMSCA 所获得结果仍优于其他算法.而从图2中的最后两行也可以看出,IMSCA在DTLZ1 测试函数的表现较为良好.表3统计了各算法在13个测试函数上采用SP指标的统计结果.对于SP指标,其值越小,表示算法解得分布越均匀,如果SP值为0,则表示所有解都是等距排列的.从表3可以看出,IMSCA算法包揽了大部分测试函数的最优值,MOEA/D算法表现也比其在IGD指标下的表现更为优秀.对于ZDT测试函数,IMSCA,MOEA/D与IM-MOEA包揽了全部的最优值,对于ZDT1和ZDT6,IMSCA表现良好并包揽了两个测试函数在SP指标下最优值.而对于ZDT2,ZDT3与ZDT4测试函数,尽管SP指标下的最优值为MOEA/D与IM-MOEA所获得,但根据秩序检验的结果,他们所获得的结果与IMSCA所获得的结果无明显差异.对于UF4测试函数,尽管NSGA-II获得了最优值,但IMSCA仍然优于大部分算法如MOEA/D,AGE-II等.而对于UF5和UF6测试函数,IMSCA在SP指标下的表现稍逊于MOEA/D,但仍然优于其他算法如NSGA-II 等.对于UF7-9测试函数,IMSCA的表现明显优于大部分算法,由表3 可以看出,三个测试函数在SP指标下的最优值全部为IMSCA算法所获得.最后对于DTLZ1和DTLZ2测试函数,尽管NSLS与NSGA-II的表现良好,但IMSCA算法依然优于大部分算法.总体来讲,IMSCA算法通过采用正余弦函数来不断更新位置,并通过采用了OBL和GGR机制来进一步强化算法的收敛性,从而提升了算法的性能. 图2 各算法部分测试函数所获非支配解情况Fig.2 Pareto fronts of each algorithm on parts of hard test instances 表2 各算法在IGD指标下的统计结果,其中灰色标记部分为最优值Table 2 IGD metric results obtained by each algorithms 表3 各算法在SP指标下的统计结果,其中灰色标记部分为最优值Table 3 SP metric results obtained by each algorithms 在IMSCA算法中,我们引入了全局网格机制,其中通过参数h来划分网格,构建网格坐标.因此我们将通过在ZDT3,UF4,UF9和DTLZ2上的实验来分析参数h的影响,并试图提供一个合适的参数设置.为了避免偶然性,我们在这里设定h∈[5,30).此外,我们首先生成一系列随机值来设置其它控制参数,并将其在实验中保持不变来保证实验的客观性. 如图3为IMSCA算法的IGD值随h取值变化的规律图.从图中可以看出,算法的IGD值从开始变化到h=5左右迅速下降,然后上升直到边界.从图中可以看出,IMSCA算法对双目标问题和三目标问题的参数灵敏度相似,尽管算法在IGD取最好的值时参数h不完全一样,但大体上是相似的.综上所述,IMSCA算法在h∈[9,11]时对于双目标和三目标问题较为合适. 本节将提出的IMSCA算法应用到实际的减速器优化设计问题中,并与四种已实现的算法(NSGA-II,MOPSO[23],MOALO[24],PAES)进行了对比与分析,进而验证本算法的良好性能. 减速器优化设计问题是工程领域中一个较为突出的优化设计问题,该问题主要包含两个目标最小化:减速器的重量f1 与应力f2.此外该问题还包含7个设计变量即齿轮面宽度x1、 齿模x2、 小齿轮的齿数x3、轴承1的间距x3、轴承2的间距x4、轴1的直径x5、轴2的直径x6.其具体描述如[25]: (12) (13) 约束条件为: 其中,2.6≤x1≤3.6,0.7≤x2≤0.8,17≤x3≤28,7.3≤x4≤8.3,7.3≤x5≤8.3,2.9≤x6≤3.9,5.0≤x7≤5.5. 在本节中,四种算法在减速器优化设计问题上的运行代数为1000,为避免偶然性,每个算法单独运行30次,并做统计分析.此外,除去本文已介绍的SP指标,本节还引入了世代距离GD指标[24]来客观的评价各算法在该真实工程问题上的表现.其具体结果如表4所示. 如表4所示为MOPSO,NSGA-II,MOALO,PAES和IMSCA算法在减速器优化设计问题上实验结果,其在GD和SP指标独立运行30次的平均值与标准差已经列在表中,灰色高亮标记表示该指标下的最优值.从表中的数据可以看出,IMSCA在GD指标和SP指标上都取得了最好的解,尽管MOALO在该问题上的表现也较为良好,但对比本文提出的IM-SCA算法,仍有一些劣势.这主要是由于MOPSO,NSGA-II,PAES以及MOALO算法单纯使用了进化的操作来对数据进行优选,但面对复杂约束问题,其很难达到较好的效果.而本文提出的IMSCA算法,一方面继承了原有SCA算法的良好性能,另一方面两种不同的机制:基于反向学习机制与基于网格密度筛选机制的引入都进一步巩固与强化了算法解的收敛性与多样性,从而在实际问题中取得了较好的效果. 为了进一步提升算法的收敛性并一定程度的保持解得多样性,本文提出了一种改进的正余弦多目标优化算法IMSCA.算法继承了原有单目标SCA算法在目标空间的良好收敛能力,并通过采用基于反向学习的机制重新设计了算法初始化阶段,此外,结合我们之前的工作,本算法还提出了一种基于网格密度的新机制,通过计算全局网格排序与网格密度排序进一步筛选出优良个体,从而强化和巩固算法的收敛性和多样性. 最后,本文通过对IMSCA和其他5种先进的进化算法进行了广泛的实验比较,并选取了ZDT,UF,DTLZ的部分测试基准问题来研究和评估算法的能力,最后算法还在实际的减速器优化设计问题上进行了实力验证.统计结果显示,本文提出的IMSCA算法在测试问题和实际优化问题上都表现出了良好的性能与潜力.但是,在本文采用的实例上表现良好,并不代表其可在所有的实例中表现良好,不同的实际问题与环境更需要针对性的选择与设计算法.在未来,我们将扩展IMSCA,通过结合约束处理技术解决高维约束多目标问题,以进一步验证其有效性.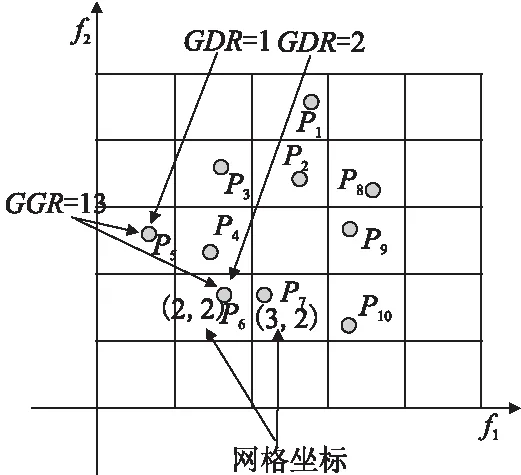
3.4 外部解集更新
4 实验设计
4.1 参数设定
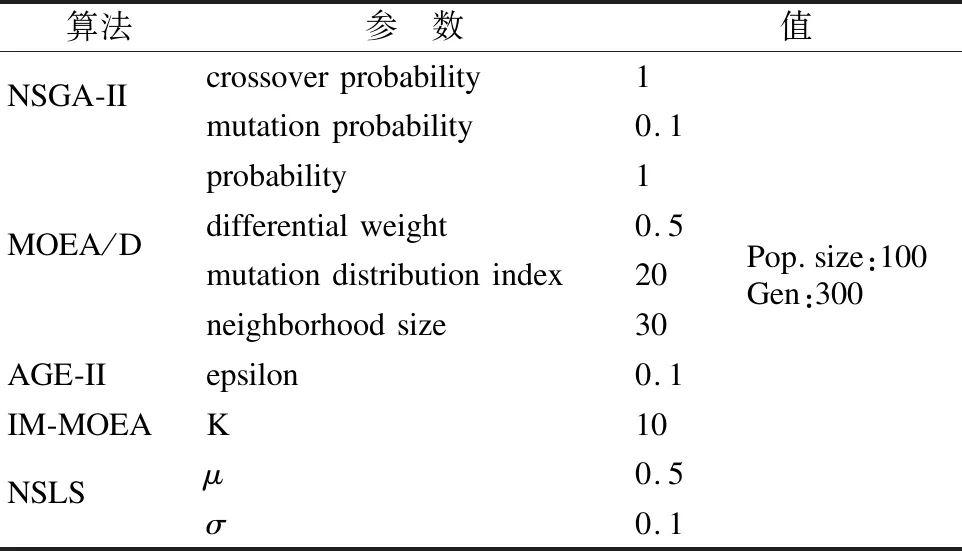
4.2 结果分析
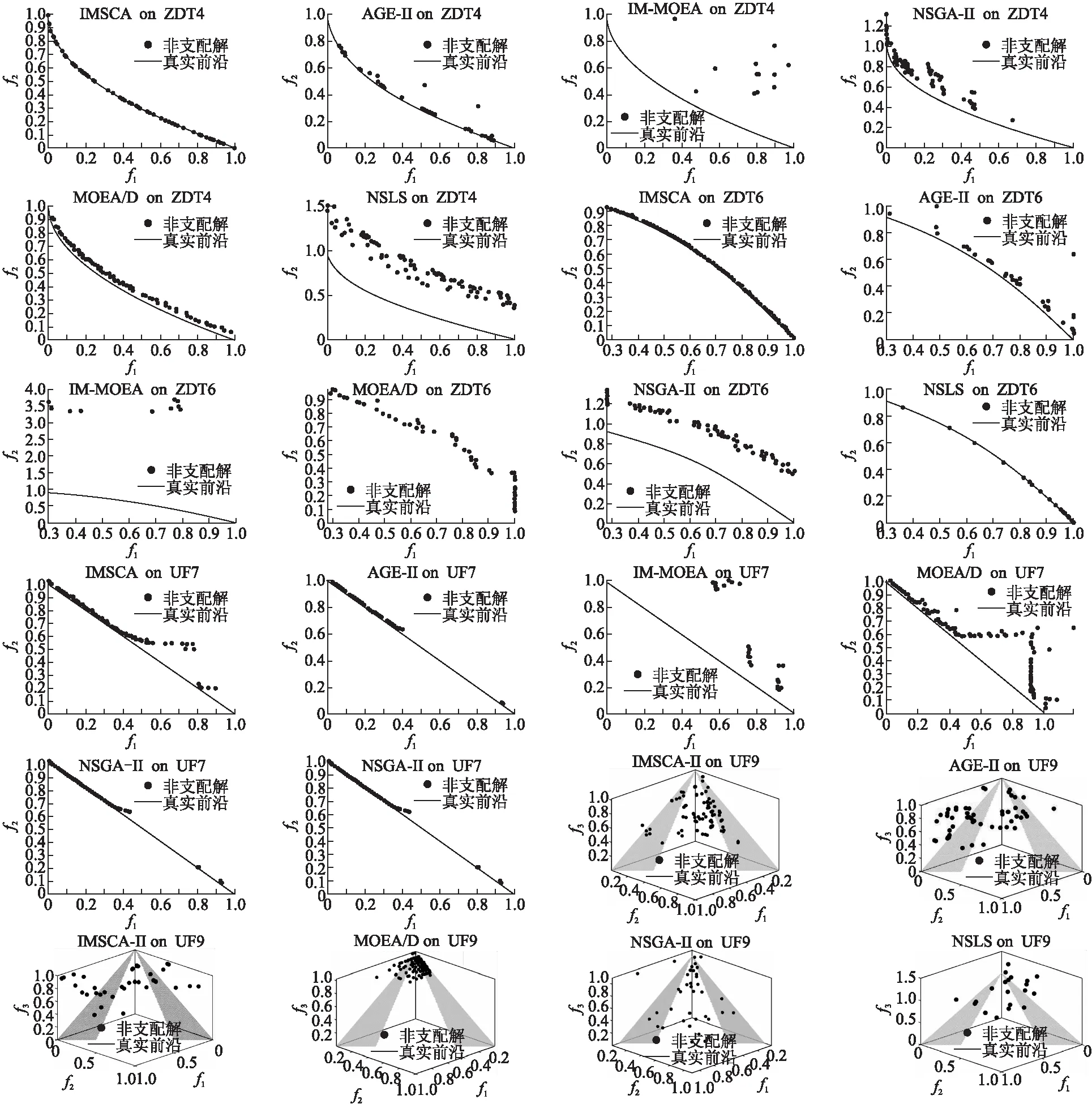

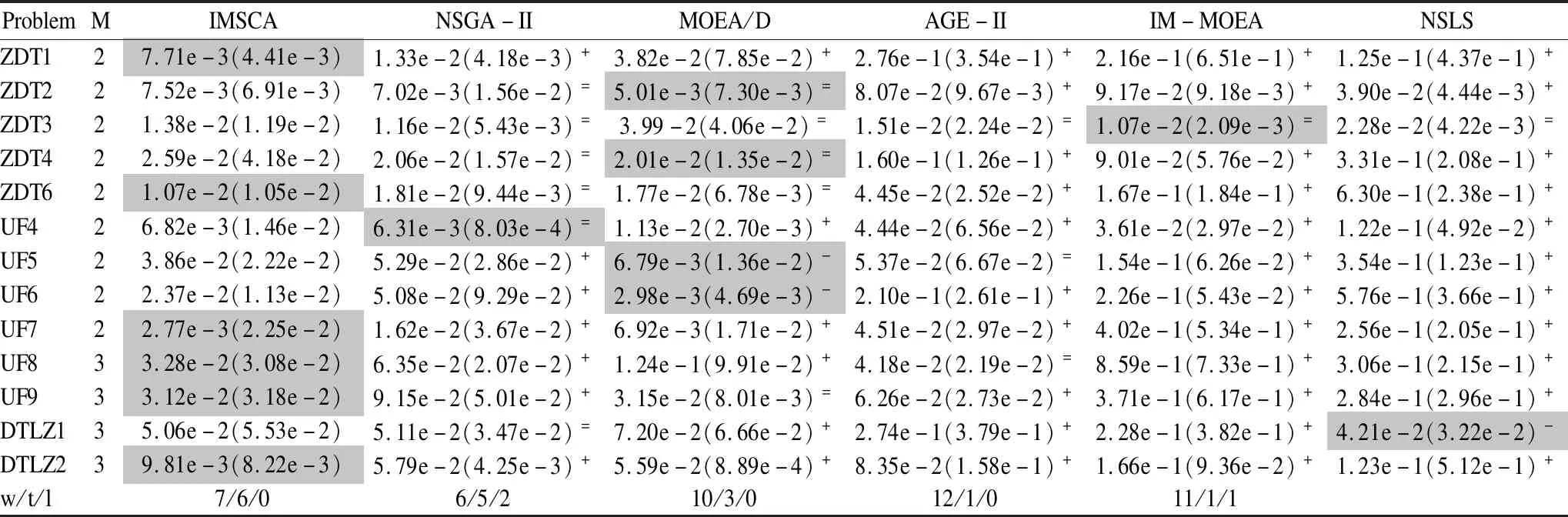
4.3 参数分析
5 工程实例应用
6 总 结
