交换半环上矩阵I+XY的正行列式|I+XY|+与负行列式|I+XY|-关系的一个注记

刘一瑾, 吴 莉, 王学平*

(1. 四川师范大学 数学科学学院, 四川 成都 610066; 2. 阿坝师范大学 数学与计算机科学学院, 四川 成都 623002)

行列式在域和环上线性代数的求解及工程技术中有着极其重要的作用[1-2].半环上矩阵的行列式也同样重要,Tan[3-4]在系数矩阵可逆的条件下用行列式给出了一些特殊半环上求解线性方程惟一解的Cramer法则.由于半环的元关于加法一般无负元,所以不能像在域和环上那样去定义半环上矩阵的行列式.为此,1972年,Kuntzman[5]在半环上引入了矩阵的双行列式的概念.2010年,Perfilieva等[6]用双行列式给出了矩阵秩的概念,并由此给出了半环上线性方程有解的一个必要条件.特别地,Wang等[7]和Shu等[8]不但给出了矩阵双行列式不为零的充要条件,还在系数矩阵的双行列不为零的条件下给出了求解半环上线性方程惟一解的Cramer法则.Poplin等[9]就交换半环上矩阵行列式等式做了详细的研究,包括Cauchy-Binet和Laplace定理以及矩阵乘积的行列式等式和伴随矩阵等,并在论文最后提出了开问题:I+XY的正行列式|I+XY|+与负行列式|I+XY|-具有怎样的关系?本文探讨了在交换半环上矩阵I+XY的正负行列式的展开形式以及其关系,回答了这一问题.

1 预备知识

定义 1.1[10]一个半环是带有2个二元运算的代数系统(R,+,·,0,1)且满足下列条件：

1) (R,+,0)是一个交换幺半群;

2) (R,·,1)是幺半群;

3) ∀a,b,c∈L,a(b+c)=ab+ac,(b+c)a=ba+ca;

4) ∀r∈L,0·r=r·0=0;

5) 0≠1.

如果任意的r,r′∈R,都有r·r′=r′·r,则称半环R是交换的.如果任意的a,b∈R,由a+c=b+c可推出a=b,则称元c是加法可消的.如果R的所有元都是加法可消的,那么称半环R是可消的.

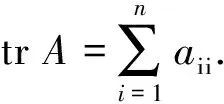
其中，Sn为n阶对称群，An为n阶交错群.

引理 1.1[9]设A=[a1,…,an]∈Mn(R)且ak=bk+ck,则

|A|±=|a1,…,ak-1,bk,ak+1,…,an|±+

|a1,…,ak-1,ck,ak+1,…,an|±.

引理 1.2[9]设A∈Mn(R),则

(列q+)|A|+=a1qAπ(q+1)1q+

a2qAπ(q+2)2q+…+anqAπ(q+n)nq,

(列q-)|A|-=a1qAπ(q)1q+

a2qAπ(q+1)2q+…+anqAπ(q+n-1)nq.

引理 1.3[9]若A∈Mm×n(R),B∈Mn×m(R),并且C=AB∈Mm(R),则

|Cα

|Cα

其中γ=(i1,…,ik)(1≤ir≤n,1≤r≤k).

引理 1.4[9]设A,B∈Mn(R),则

|AB|++|A|+|B|-+|A|-|B|+=

|AB|-+|A|+|B|++|A|-|B|-.

2 |I+XY|+与|I+XY|-的关系

本节主要探讨I+XY的正负行列式的展开形式,以及|I+XY|+与|I+XY|-在交换半环上的关系.

定理 2.1若X∈Mm×n(R),Y∈Mn×m(R),则|I+XY|+与|I+XY|-有如下关系：

其中γ=(i1,…,ik)(1≤ir≤n,1≤r≤k).

证明令XY=[z1,…,zm],I=[e1,…,em],则

I+XY=[e1+z1,…,em+zm].

由引理1.1有

|I+XY|+=|e1+z1,…,ek-1+zk-1,

ek+zk,ek+1+zk+1,…,em+zm|+=

|e1+z1,…,ek-1+zk-1,ek,

ek+1+zk+1,…,em+zm|++

|e1+z1,…,ek-1+zk-1,zk,

ek+1+zk+1,…,em+zm|+.

每个行列式均可按第k列的ek+zk拆成2个矩阵的行列式(k=1,2,…,m),这2个矩阵的第k列分别为ek和zk,由此递推可知|I+XY|+最终可分为2m个行列式之和,即

|I+XY|+=|e1,…,em|++|z1,e2,…,em|++

|e1,z2,e3…,em|++…+

|e1,…,em-1,zm|++

|z1,z2,e3,…,em|++|z1,e2,z3,e4,…,em|++

…+|e1,…,em-2,zm-1,zm|++…+

|e1,z2,…,zm|++|z1,e2,z3,…,zm|++

…+|z1,…,zm-1,em|++|z1,…,zm|+.

(1)

又由引理1.2知每个行列式可看作是去掉r行和r列的余子阵的正行列式,如

|e1,…,er,zr+1,…,zm|+=

|(XY)(1,2,…,r|1,2,…,r)|+.

故

|I+XY|+=1+|(XY)(2,…,m|2,…,m)|++

|(XY)(1,3,…,m|1,3,…,m)|++…+

|(XY)(1,…,m-1|1,…,m-1)|++

|(XY)(3,…,m|3,…,m)|++

|(XY)(2,4,…,m|2,4,…,m)|++…+

|(XY)(1,…,m-2|1,…,m-2)|++…+

|(XY)(1|1)|++|(XY)(2|2)|++…+

|(XY)(m|m)|++|XY|+=

(2)

同理可得

|I+XY|-=|e1,…,em|-+|z1,e2,…,em|-+

|e1,z2,e3…,em|-+…+|e1,…,em-1,zm|-+

|z1,z2,e3,…,em|-+|z1,e2,z3,e4,…,em|-+

…+|e1,…,em-2,zm-1,zm|-+…+

|e1,z2,…,zm|-+|z1,e2,z3,…,zm|-+

…+|z1,…,zm-1,em|-+|z1,…,zm|-=

0+|(XY)(2,…,m|2,…,m)|-+

|(XY)(1,3,…,m|1,3,…,m)|-+…+

|(XY)(1,…,m-1|1,…,m-1)|-+

|(XY)(3,…,m|3,…,m)|-+

|(XY)(2,4,…,m|2,4,…,m)|-+…+

|(XY)(1,…,m-2|1,…,m-2)|-+…+

|(XY)(1|1)|-+|(XY)(2|2)|-+

…+|(XY)(m|m)|-+|XY|-=

(3)

为了书写方便,可记

|(XY)(i1,…,ik|i1,…,ik)|=|(XY)αα|,

其中α=(i1,…,ik)1.因此由(2)和(3)式可得

(4)

又由引理1.3有

|(XY)α

|(XY)α

再由(4)式可得

以下以二阶矩阵为例加以验证.设

则

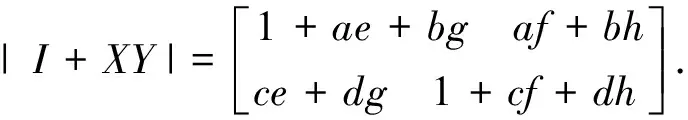
由正负行列式公式知

|I+XY|+=(1+ae+bg)(1+cf+dh)=

1+acef+bdgh+adeh+

bcgf+ae+bg+cf+dh,

|I+XY|-=(af+bh)(ce+dg)=

acef+bdgh+adgf+bceh,

则有

|I+XY|++adgf+bceh=

|I+XY|-+1+

adeh+bcgf+ae+bg+cf+dh.

又由于

|X|+=ad, |X|-=cb,

|Y|+=eh, |Y|-=gf,

trXY=ae+bg+cf+dh,

从而

|I+XY|++|X|+|Y|-+|X|-|Y|+=

1+|I+XY|-+|X|+|Y|++

|X|-|Y|-+trXY,

(5)

即为

其中γ=(i1,i2)(1≤ir≤2,1≤r≤2).符合定理2.1中的等式.

推论 1设R是交换可消半环,若A是R上的二阶矩阵,则

|I+A|++|A|-=

1+|I+A|-+|A|++trA.

(6)

证明设X、Y是R的二阶矩阵,将|XY|++|XY|-加在(5)式两边可得

|I+XY|++|X|+|Y|-+|X|-|Y|++

|XY|++|XY|-=

1+|I+XY|-+|X|+|Y|++|X|-|Y|-+

|XY|++|XY|-+trXY,

由引理1.4知

|XY|++|X|+|Y|-+|X|-|Y|+=

|XY|-+|X|+|Y|++|X|-|Y|-,

则

|I+XY|++|XY|-=

1+|I+XY|-+|XY|++trXY.

令A=XY,则

|I+A|++|A|-=1+|I+A|-+|A|++trA.