区域PM2.5时空回归建模与预测

王德冬，秦 聪

1. 山东省遥感技术应用中心，山东 济南 250013 2. 山东光庭信息技术有限公司，山东 烟台 264000

近年来，大气环境质量已成为社会关注的热点问题之一。从2013年开始，我国政府陆续向大众发布从各城市监测站点测得的实时大气颗粒物浓度数据，到目前为止，全国已布设 1 600个监测站点，越来越多的研究开始关注区域PM2.5的污染状况及其时空分异特征，如王振波等[1]基于全国190个城市中945个监测站的观测数据，采用空间数据统计模型揭示了2014年中国城市PM2.5浓度时空变化规律，发现PM2.5浓度在时间上呈现显著的冬秋高、春夏低“U”型变化规律与显著的空间分异与集聚规律；杨冕等[2]运用地理学时空分析与GIS可视化方法探索并呈现了2015年长江经济带PM2.5的时空分布特征及其演变规律；徐伟嘉等[3]利用空间地统计方法，分析了珠三角区域PM2.5时空分异特征；徐建辉等[4]利用MODIS遥感数据对长三角PM2.5浓度进行了建模和估算，并分析了其时空分布特征；刘永林等[5]利用17个空气质量监测站数据分析了重庆市主城区PM2.5时空分布特征。

大部分研究均是根据原始监测点数据对区域PM2.5进行时空分异特征研究，当需要获得某段时期内(如月份、季节和年)空间连续型分布数据时，往往采用空间插值方法对样点均值进行空间插值得到。这种处理方法忽略了样点本身存在的时空相关性和变异性，丢失了大量时空变化信息，而且得到的只是某时期内均值的空间分布信息，难以进行更为深入的时空分析。针对这一点，梅杨等[6]利用监测数据对山东省2014年PM2.5浓度进行了时空建模及插值，得到了区域PM2.5时空立方体数据，进而进行了时空分析，总结了山东省PM2.5时空分布特征。此研究为获取区域PM2.5时空立方体数据提供了一条途径。同时，注意到虽然时空地统计方法插值结果会高于只使用同一时期样点的空间地统计方法，但由于一般区域的监测点数量相对于区域面积来讲，较为稀疏，因此时空估值精度仍然较低，如上述研究中，时空克里格估值的均方根误差为22.08 μg/m3，相对于区域时空样点均值74.84 μg/m3仍然较高。因此，如何提高区域PM2.5时空估值精度，进而提高时空分析的可靠性，十分值得研究。

同时，注意到上述关于区域PM2.5的研究，均揭示出由于地理位置特征和季节的气候差异，PM2.5存在显著的时空分布趋势，而对其他环境属性的地统计建模和分析研究中，往往考虑了空间或时空趋势的估值结果要高于忽略了这些趋势的结果[7-9]。基于上述考虑，本文拟利用时空回归克里格对区域PM2.5进行时空建模及插值，目的基于监测数据提出PM2.5时空分布趋势模型；对剥离趋势后的时空样点残差建立时空变异模型，并利用时空普通克里格方法进行插值；将时空分布趋势与残差的克里格插值结果，作为最后的预测结果；与不考虑时空趋势模型的时空普通克里格插值进行精度对比，分析所提方法优势与不足。

1 时空回归克里格方法

1.1 时空环境变量定义

在时空随机场下，定义时空环境变量：

z(p):p=(s,t),s=(s1,s2)∈S,t∈T

(1)

式中：p表示时空位置；z(p)表示p位置处时空变量；s和t分别表示空间坐标和时间；s1和s2分别表示空间坐标中2个横、纵坐标分量；s和T分别表示空间域和时间域。当s和t确定时，就认为取得了一次时空变量的实现(即观测值)。同时，为了研究环境变量的时空趋势及其对时空预测及制图的影响，环境变量被定义为趋势项和残差项之和：

z(p)=m(p)+R(p)

(2)

式中m(p)和R(p)分别表示趋势项和残差项。在没有任何辅助数据的支持下，根据KYRIAKIDIS等[10]的研究，关于时空位置的2次多项式已经足够表达地理属性的时空分布趋势。因此本研究中，将PM2.5的时空分布趋势表示为：

m(p)=m(s1,s2,t)=a1+a2s1+a3s2+a4s1s2+

a5s12+a6s22+a7t+a8t2+a9ts1+a10ts2

(3)

式中的系数ai将根据建模样点、利用matlab的趋势分析技术拟合。

1.2 时空克里格方法

对所有参与建模的样点，减去样点位置处的时空趋势后，得到样点残差R(p)，基于此，计算各时空滞后距的经验时空半方差值：

(4)

式中：hs和ht表示空间和时间上的滞后距；N(hs,ht)表示时空样点中符合上述滞后距的点对数量；γ(hs,ht)表示在时空滞后距hs和ht上的经验时空半方差值。计算若干组不同时空滞后距的时空实验变异函数后，形成时空实验变异函数散点图。为了获取任意时空滞后距上的时空变异函数值，需利用该散点图，拟合理论时空变异函数模型，本文选取的模型形式：

(5)

上述模型中各参数(c0,c,v,w,ξ)拟合后，联合时空样点，基于时空克里格法对待估时空位置的PM2.5残差进行估值，克里格矩阵：

(6)

式中:p0为待估时空位置;pi(i=1,…,n)为p0周围的n个时空样点的位置;λi为需要求取的样点的权重系数。n一般取4～8，因为由于屏蔽效应，过多的邻近点对插值结果影响不大，在本文中n取8。解该矩阵，得到λi的值，则p0时空位置处的估计值z*(p0)：

(7)

1.3 精度比较

为比较趋势分析和回归克里格的插值精度，同时使用原始样点数据按照式(4)的方式计算实验变异函数，并拟合式(5)的理论模型参数，最后用式(6)对各待估时空位置进行时空估值。对实验数据，使用十叠交叉验证法对比2种方法所得精度，即每次预留10%的监测站(即5个)，将其所有监测数据作为验证数据集，其余作为建模数据集，对比2种方法所得的均方根误差，以此来评价2种方法所得精度。

1.4 实验数据

以苏南地区2014年PM2.5日监测数据为实验数据，该地区共有大气监测站53个，监测站空间分布如图1所示，其统计特征如图2所示。2014年，苏南地区PM2.5的最大值和最小值分别为5 μg/m3和531 μg/m3，均值为65.6 μg/m3。

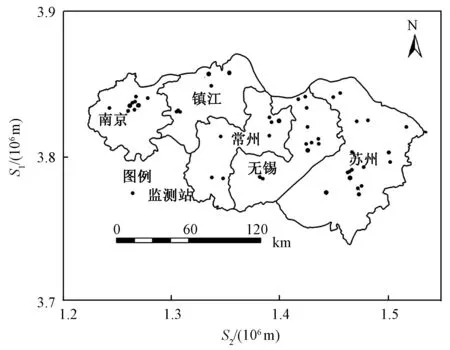
图1 苏南地区大气监测站空间分布图Fig.1 Spatial locations of the monitoring sites in southern Jiangsu during 2014

图2 苏南地区大气监测数据统计特征Fig.2 The summary statistics and histogram of the PM2.5 concentrations of all the collected data in southern Jiangsu during 2014

2 结果与讨论

因为使用的是十叠交叉验证法，因此所有建模和插值被计算了10次，为使文章简洁，仅展示第一次实验的计算结果。

2.1 时空趋势建模

依据式(3)，建立研究区PM2.5与时空位置间的趋势模型m(s1,s2,t)=49.56-1.879×10-4s2+5.448×10-5s1+4.298×10-11s1s2-3.788×10-11s22-3.879×10-12s12-1.487×10-5t+9×10-4t2+3.468×10-7s2-2.499×10-7ts1。

图3展示了该趋势模型的整体结果及其从西到东的三维效果。从图3可以看出，时间上该地区PM2.5呈现明显冬、春季高，夏、秋季低的“U”型变化规律，空间上从东到西呈递增趋势。这是因为，苏南地区东部靠海，受到风力和温度的影响，东部地区PM2.5浓度相对西部较低。同时，用建模点趋势值与实际值的平均绝对误差(MAE)、平均误差(ME)和相关系数(r)来量化建模效果。其中ME为0.003，说明建模点实际值均匀地分布在所得趋势(体)的上下方；MAE为18.76，相对于该地区PM2.5样点均值65.63还是较高，说明有的监测点实测值距离所得趋势(体)较远，误差较大。

2.2 时空变异模型

对建模组的样点残差，计算K-S的值为2.79，表明样点残差接近正态分布，因此可用残差直接进行变异函数的计算和后续的时空插值。而原始样点经检验不符合正态分布，但对数转换后的数据接近正态分布。按照式(4)计算各时空滞后距上残差和lgPM2.5的变异函数值，并拟合式(5)的理论模型，其结果如图4所示。从图4可看出，代表经验变异值的黑色散点紧紧围绕在代表理论时空变异模型的曲面周围，说明理论模型拟合较好，能够表达区域PM2.5残差和原始数据的时空变异特征。另外，从图4可看出，时间上，残差和 lgPM2.5的变异值在0～4 d呈递增趋势，但4 d以后变异值区域平稳，说明时间上有效相关范围为4 d左右。而空间上，这种递增趋势持续到150 km，说明空间上的有效相关范围至少有150 km。

图3 2014年苏南地区PM2.5时空分布趋势模型整体结果及其从西到东的时态分布趋势Fig.3 (a) ST trend model of PM2.5 concentrations in southern Jiangsu province, China, during 2014, and (b) the temporal trend for PM2.5 concentrations during 2014 in southern Jiangsu province, China.

图4 残差与取对数后的原始样点的经验时空变异函数值(散点)与拟合的理论时空变异函数模型(曲面)Fig.4 Empirical variogram values (black dots) of the PM2.5 residuals (a) and logPM2.5 (b), and the theoretical variogram model (surface) fitted to these empirical values.

2.3 时空插值

本研究中设置得待插值时空网格为2 km × 2 km × 1 d，基于上述的理论时空变异模型，按照式(6)和式(7)对每个时空网格的残差和lgPM2.5进行估值。其中logPM2.5的估值结果进行幂函数转换后，得到不考虑时空趋势的PM2.5时空分布立方体数据，如图5(b)所示。而对于残差的估值结果，加上每个时空网格出由式(8)计算而来趋势值，得到考虑时空趋势的时空回归克里格估值结果，如图5(a)所示。

图5 基于时空回归克里格和时空普通克里格的PM2.5时空分布图Fig.5 Plot of the ST map of predicted PM2.5 concentration generated by the spatiotemporal kriging with trend and spatiotemporal ordinary kriging

2.4 精度评价

使用十叠交叉验证进行了精度验证，即每次预留5个监测站的观测数据作为验证数据集，其均方根误差的结果如图6所示。其中时空普通克里格方法(STOK)的平均均方根误差为14.27，而时空回归克里格(STRK)的平均均方根误差为12.43。因此，STRK的插值精度优于STOK的插值精度，精度平均提高12.9%。

图6 STKT和STOK的十叠交叉验证结果Fig.6 The results of 10-fold cross validation of STKT and STOK

2.5 讨论

本研究的创新之处在于构建了区域PM2.5的时空趋势模型，它很好地表达了区域PM2.5的时空分布趋势特征，并且有效地消除了PM2.5的时空非平稳性。而平稳性假设或二阶平稳性是地统计学的基本假设，预测结果的误差正是来源于地理属性或环境变量对这些假设的背离，背离程度越高，精度越低。而关于PM2.5的区域性研究或插值，往往涉及的空间和时间范围很大，这种地理上和时态上的差异使得原始数据很难符合二阶平稳性假设的2个条件，即区域化变量的均值存在且平稳，增量的方差存在且平稳。而趋势模型在一定程度上表达了区域PM2.5的均值分布，将其剥离后，能够使残差的均值较原始数据更为平稳(接近于0)，这可能是造成时空回归克里格精度更高的原因之一。

当然，本研究也存在不足之处：一是所得的趋势模型精度仍然不高，这是因为造成PM2.5时空差异的因素众多，其分布不但与时空位置相关，还与与社会经济及气候等多种因素相关[11-13]。因此，如何综合更多数据(如社会经济统计数据、气候数据、地形地貌数据等)来建立更为精确的趋势模型，将对提升时空估值精度有较大帮助；二是大气监测站的位置一般在城市，因此可能会造成农村或山区估值精度降低。而且由于城市人口、交通、工业更为密集，可能会造成农村或山区估计值大大高于其真实值。这就需要寻求与PM2.5密切相关且能全区域大范围覆盖的辅助要素参与建模与估值。近年来的研究发现，基于遥感的气溶胶光学厚度数据与PM2.5具有显著相关性[14-17]。因此，可以考虑将其纳入PM2.5时空建模和估计中去，提升未设监测站区域的估值精度。但目前实施起来尚有阻碍，原因是这些辅助数据在区域时空范围内有缺失，如气溶胶数据为10 km×10 km的形式呈现，且并不是所有位置和所有时间都有数据存在，即这些数据并不能完全遍布整个区域的时空范围。那么，如果气溶胶参与了趋势模型的构建，那么在无气溶胶观测数据的时空位置，则无法依据该模型得到PM2.5的趋势值。因此，如何融合这些数据进行PM2.5时空建模与估值，需要进一步研究。

3 结语

本文利用时空回归克里格对区域PM2.5进行了时空建模及估值，建立了PM2.5与时空位置的多元非线性关系，得到了区域PM2.5时空分布趋势；计算样点残差的实验变异函数并拟合了理论变异函数模型；对残差进行时空克里格插值；将残差的插值结果与趋势模型结果相加，得到区域PM2.5时空回归克里格估值结果。与不考虑趋势的时空普通克里格结果相比，其预测精度提升了18.58%，为更精确地进行区域PM2.5时空分析提供了更为可靠的数据基础。