信噪比信息与时频特征修正相位的语音增强

贾海蓉，王卫梅，吉慧芳

(太原理工大学 信息与计算机学院，山西 太原 030024)

在过去的三十年中，单通道语音增强的研究主要集中在对语音谱幅值的估计，而忽略了对相位的信息处理，近几年相关文献证明相位信息与语音的可懂度密切相关[1]。随着纯净语音相位估计的准确性对抑制噪声的影响越来越重要，在语音增强中使用相位估计重建信号改进性能的方法也不断被提出[2-3]。经典方法包括基于谐波模型的相位重构的语音增强方法[4]，用带噪语音相位代替清音段语音相位，在一定信噪比范围内提高了语音质量，但同时造成了语音不连贯的问题，导致了语音失真；未封装相位的时间平滑的语音[5]方法，是先对带噪语音的瞬时相位谱进行相位分解，再通过时间平滑减小噪声相位，从而重构出增强的瞬时相位谱用于信号重构；具有相位约束的几何方法[6]，利用基频和相位畸变特征进行谐波增强的相位重构方法[7]，是通过考虑谐波相位谱的关系来估计语音相位谱，改善了各种噪声环境下的语音质量。文献[8]通过计算加入与输入信噪比变化相关的相位补偿函数，对语音的相位进行补偿，最终实验证明，在低信噪比下依然可以有效去除噪声。上述几种方法都不同程度地改善了语音质量，但对于语音失真和可懂度方面还有待提高。另外，相位估计除了对信号重建的积极影响外，最近的几项研究表明，它从带噪语音中能更准确地估计谱幅度的有效性[9-11]。文献[12]通过实验证明提出的相位信息的复谱语音系数的估计量对提高含噪语音的感知质量和可懂度有显著作用。文献[13]综述了相位谱信息在语音增强等语音处理应用领域的广泛应用。

对此，针对传统基于谐波模型的相位重构算法在提高语音质量的同时引入语音失真、导致语音连贯性差的问题，文中利用信噪比信息和时频特征重构谐波相位模型，其中时频特征与相位失真密切相关，为减少语音失真提供了保障；为了进一步提高语音质量，提出了用改进二元假设模型的基于对数谱估计的最小均方误差准则(Minimum Mean Square Error short time Log Spectral Amplitude estimation，MMSE-LSA)估计纯净语音幅值谱；最后将重构的相位与估计的幅值相结合进行语音增强，得到信噪比高、失真较小的增强语音。

1 传统基于谐波模型的相位重构

传统基于谐波模型的相位重构算法采用非线性频率压缩的基音估计方法(Pitch Estimation method of nonlinear Frequency Amplitude Compression, PEFAC)算法[14]进行清浊音分段，得到带噪语音浊音段的近似谐波模型：

(1)

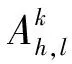
连续帧之间的相位差表达式为

(2)

其中，Mprinc{·}代表将相位差映射到[-π,π]，Arg{·}表示求相位(角)。

对浊音段每帧频带根据能量的不同分类进行讨论：

(1)若经过短时傅里叶变换后信号的能量大致集中在谐波谱上，能够使用时域的方法计算相位：

(3)

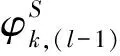
(2)若经过短时傅里叶变换后信号的能量很小，就不能把带噪语音信号的相位信息作为初始值，此时使用频域的方法计算相位：

(4)

文中选用汉宁窗，W为窗函数的频域形式，计算如下：

(5)

其中，M为窗长，Ω为频率。对式(5)取相位运算，即可得出窗函数的相位值，结合式(4)，得出相位信息的频域计算式。

其传统基于谐波模型相位重构原理图如图1所示。

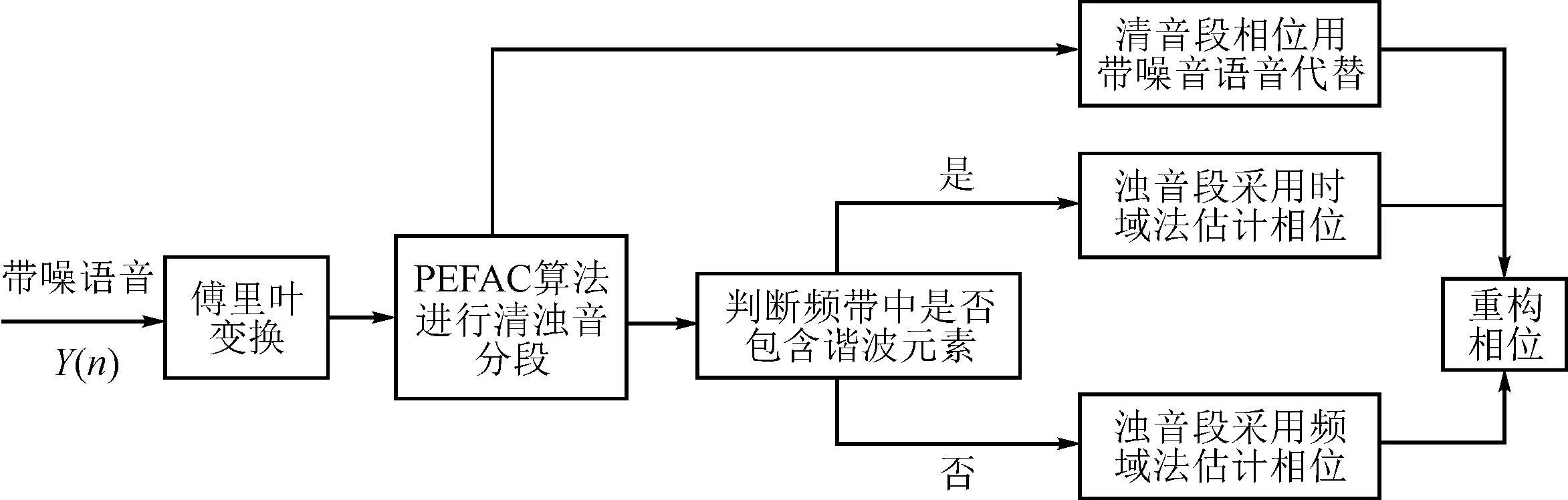
图1 传统基于谐波模型相位重构原理图

2 信噪比信息与时频特征修正相位重构的语音增强

在传统的基于模型的相位重构算法中，相位重构是只对浊音段的相位信息进行重构，而清音段用带噪语音信号的相位来近似，虽提高了语音质量，但因为没有考虑清浊音过渡段的问题，所以导致语音不连贯，使可懂度较差的问题。针对此，文中提出了用信噪比信息与时频特征改进基于模型的相位重构方法，并把它应用在语音增强中。具体步骤为：在对带噪语音用PEFAC算法[14]进行基频估计和清浊音分段的基础上，引入与相位失真相关的时频特征计算决策阈值，同时使用信噪比信息计算相位偏差；并将相位偏差与决策阈值进行比较，用于估计清音段和浊音段的语音相位；最后，结合重构的语音相位与改进二元假设模型的MMSE-LSA语音幅值估计，得到增强语音。用信噪比信息与时频特征改进基于模型的相位重构语音增强算法原理框图如图2所示。

2.1 利用时频特征计算决策阈值

将语音信号y(n)进行基音-同步信号分割[14]为t(l)段，其表达式为

t(l)=t(l-1)+1/4f0(l-1) ，

(6)

其中，f0(l-1)是第l-1帧的基频。

图2 信噪比信息与时频特征修正相位重构的语音增强框图

将谐波相位ψ(h,l)分解为3个部分,即

(7)

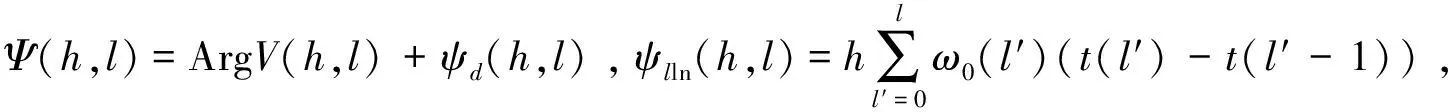
Ψ(h,l)=ψ(h,l)-ψlln(h,l) 。

(8)

由式(8)可知，用带噪语音谐波相位，减去用PEFAC算法估计出的谐波相位的线性相位部分，可计算出展开相位Ψ(h,l)。

声道滤波器的频率响应可以假设在一个音素内沿时间固定，因此，最小相位分量显示的是缓慢变化的统计量。在被噪声破坏的语音信号中，噪声的加入会污染声道滤波器的相位信息，而线性相位部分只取决于估计基频的精度。去掉了线性相位部分，通过增强带噪语音的展开相位，以减少噪声污染[10]。因此，文中将展开相位的时频特征及信噪比信息，应用于传统基于模型的相位重构算法中增强带噪语音。

定义Ψx(h,l)和Ψy(h,l)为纯净和带噪语音信号的展开相位分量。在浊音或无浊音的假设下，二元假设检验能够表述成：

(9)

(10)

其中，e(h,l)为误差项。

假设H0表示在谱相位中无谐波结构的情形，因此，可以假定谱相位均匀地分布在相位变量的范围[-π,π]内，即

p(ψy(h,l)|H0)～U[-π,π]=1/(2π) 。

(11)

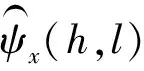
假设H1为谱相位中存在谐波的情况，且谱相位服从von米塞斯分布[13]ψy(h,l)～VM(ψμ(h,l),κ(h,l))，则有

(12)

表示噪声方差,|S(k,l)|是纯净语音幅值。

给定两个假设H1和H0，接受其中任何一个的决定是由

决定的。

(13)

其中，θth(h,l)=lnI0(κ(h,l))/κ(h,l)，为决策阈值。平均值ψμ(h,l)和浓度参数κ(h,l)所构建的von米塞斯分布模型表示的是相位的先验分布[15]，且相位的浓度参数是依赖于信噪比的。

2.2 利用信噪比信息计算相位偏差

相位几何关系图如图3所示。由图3可知

图3 相位几何关系图

(14)

根据先验信噪比ξ和后验信噪比γ的定义式，有

(15)

定义φdev=θY-θS，作为带噪语音相位θY与纯净语音相位θS间的相位偏差，且相位偏差在大于0.679rad的情况下，增强相位对提高语音的感知质量效果不明显[16]。由图3计算出几何关系为

cos(θD-θY)=(αY-x)/αD，

(16)

cosφdev=x/αS，

(17)

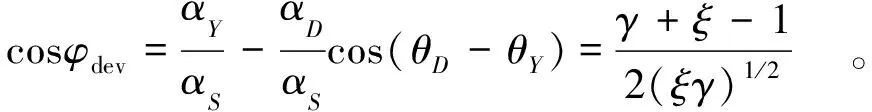
(18)

2.3 估计清音段和浊音段的语音相位

当相位偏差余弦超过由浓度参数控制的阈值时，由于相位偏差与人的感知无关，因此使用带噪语音相位来估计清音段语音相位，同时使用时域方法估计浊音段语音相位；当相位偏差余弦低于由浓度参数控制的阈值时，使用频域方法估计浊音段语音相位，同时使用相位的几何关系式来估计清音段语音相位。具体的表达为

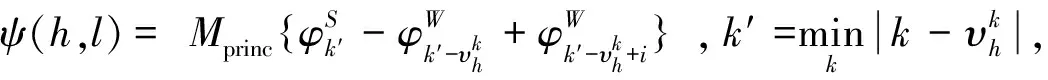
将时频特征和信噪比信息应用在相位重构中估计语音相位，既增强了感知语音质量，又提升了语音连贯性。

2.4 改进二元假设模型的MMSE对数谱幅度估计(MMSE-LSA)

根据二元假设模型用MMSE-LSA语音增强算法得到纯净语音信号Sk的估计值为

(19)

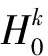
该MMSE-LSA算法虽然能够显著提高语音质量，但因为采用恒定的加权因子GDD，使谱估计不够准确，导致产生音乐噪声。为了解决这一问题，文中提出一种用改进的两步噪声消除(Two Step Noise Reduction, TSNR)的增益联合当前帧的先验信息来代替原算法中恒定的加权因子GDD，以提高先验信噪比估计的精确度，从而高度消除音乐噪声。其中，TSNR算法[17]采用基于决策导向(Decision Directed,DD)方法的结果联合系统的增益因子，从而修正对当前帧语音信号的先验信噪比估计，即

(20)

其中，GTSNR(n,k)=ξTSNR/(1+ξTSNR)；λd(k,n)是对噪声的功率谱估计。ξTSNR可表示为

ξTSNR(n,k)=|GDDY(n,k)|2/λd(k,n) ，

(21)

其中，GDD=ξDD(n,k)/(1+ξDD(n,k))。

(22)

2.5 结合重构的相位和估计的幅度增强语音

根据重构的语音相位信息和估计的语音幅度，得到最终增强后的语音信号的频域表达式为

(23)

3 实验仿真

为了验证笔者提出的新算法的有效性，实验选择在Matlab2015b的软件环境下，实验对象为863语音库中的纯净语音SP01和SP15叠加不同噪声(白噪声、Pink噪声和F16噪声)形成不同信噪比的带噪语音，其中选取采样率为8 000 Hz，汉宁窗，帧长为256，帧移为64。

首先，由于相位信息与频谱信息不同，没有明显的谐波结构，所以文中为了研究语音信号的相位信息，而将该信息可视化，利用每一帧信号的相位差值显示，如图4是对F16噪声背景下的SP15中的纯净语音相位进行重构的相位差谱图对比。其次，为了更加直观地显示算法的有效性，在F16噪声背景下，信噪比为5dB的带噪语音经文献[4]算法与文中新算法的波形对比图和频谱对比结果如图5和图6所示。最后，为了验证新算法对噪声的普适性以及在语音失真和可懂度方面的提升效果，对不同噪声背景下的SP01和SP15的带噪语音进行了测试，信噪比(Signal to Noise Ratio, SNR)和语音质量感知评估(Perceptual Evaluation of Speech Quality, PESQ)对比结果如表1和表2所示。

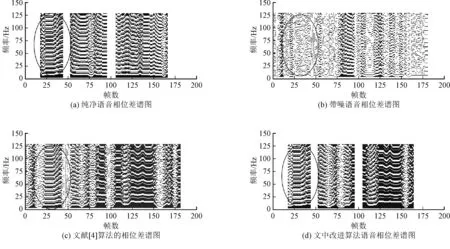
图4 文献[4]算法与文中改进算法的相位差对比谱图

图5 文献[4]算法与文中改进算法的语音增强结果波形对比图

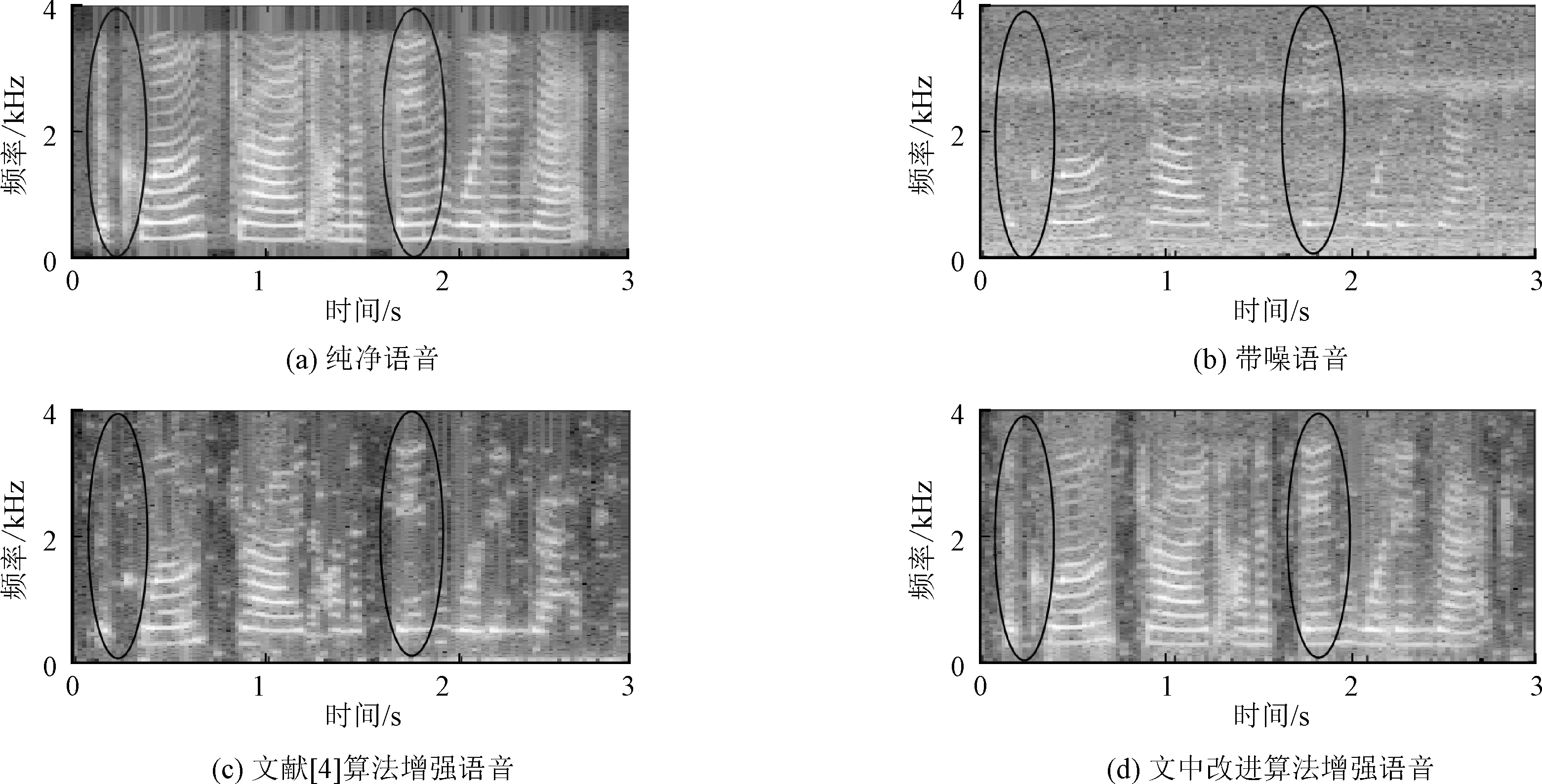
图6 文献[4]算法与文中改进算法的增强语音的语谱对比图

表1 文献[4]算法与文中改进算法的信噪比结果dB

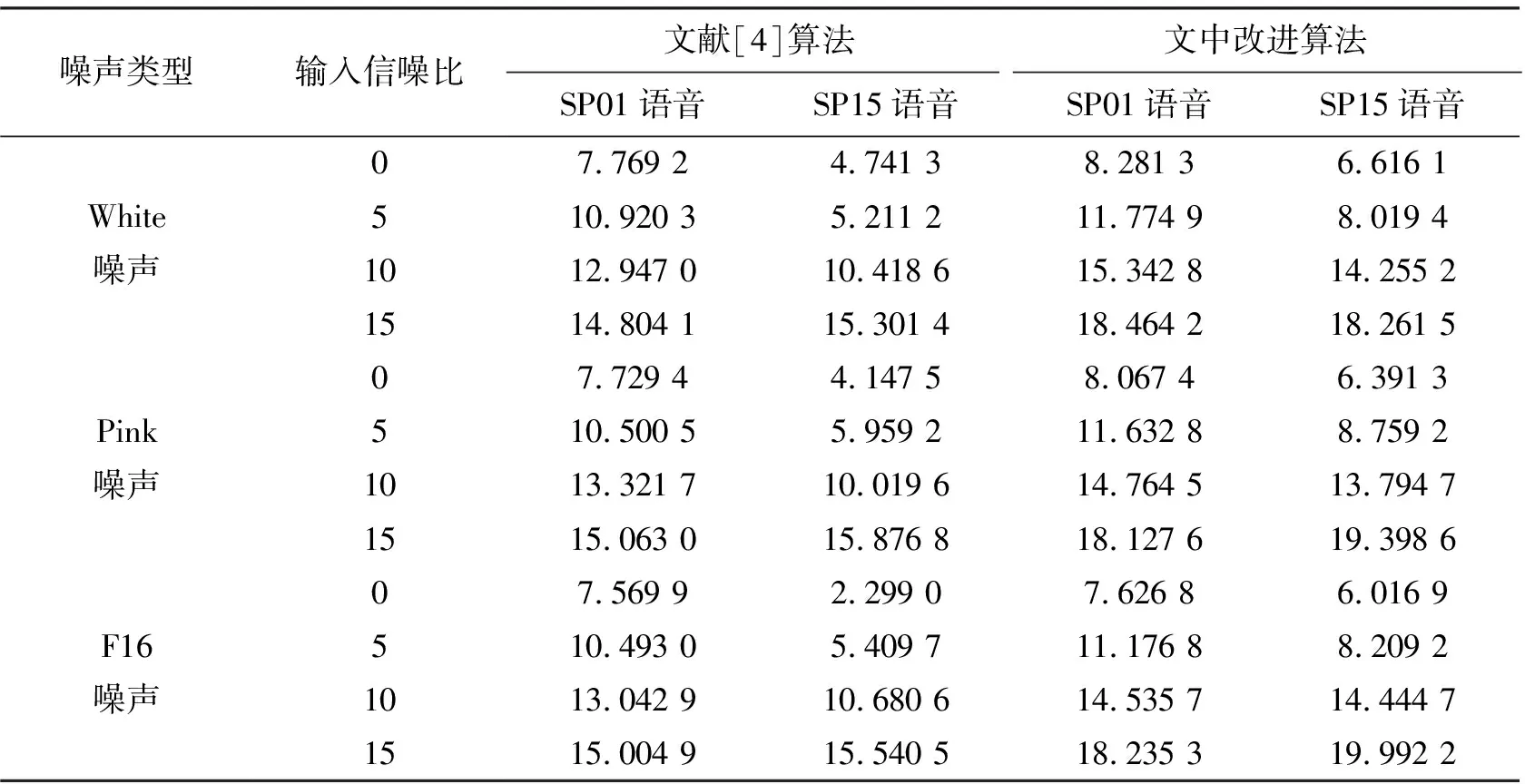
噪声类型输入信噪比文献[4]算法文中改进算法SP01语音SP15语音SP01语音SP15语音White噪声07.769 24.741 38.281 36.616 1510.920 35.211 211.774 98.019 41012.947 010.418 615.342 814.255 21514.804 115.301 418.464 218.261 5Pink噪声07.729 44.147 58.067 46.391 3510.500 55.959 211.632 88.759 21013.321 710.019 614.764 513.794 71515.063 015.876 818.127 619.398 6F16噪声07.569 92.299 07.626 86.016 9510.493 05.409 711.176 88.209 21013.042 910.680 614.535 714.444 715 15.004 915.540 518.235 319.992 2

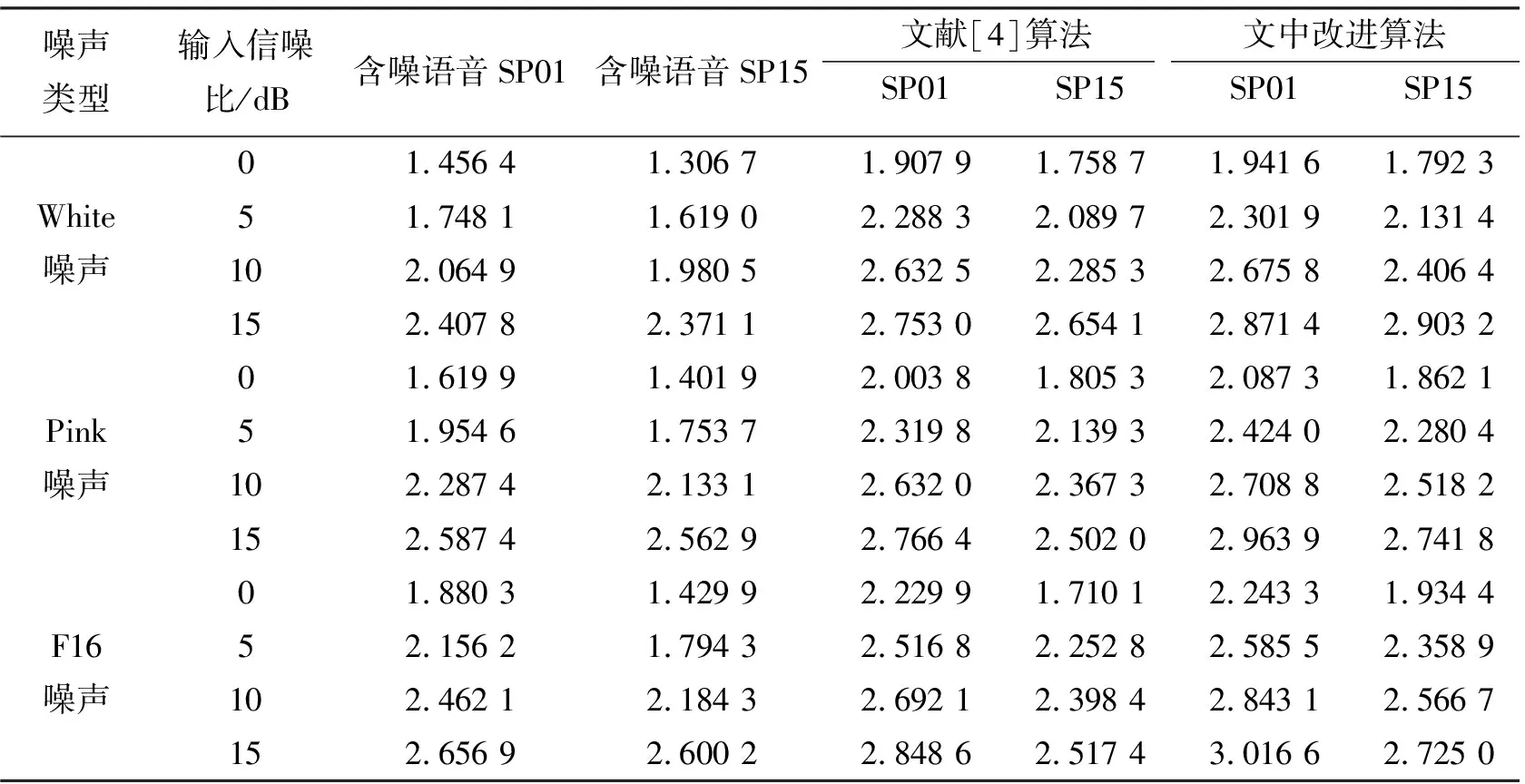
表2 文献[4]算法与文中改进算法的语音质量感知评估结果

从图4可以看出,纯净语音信号所对应的谱线非常规则且清晰，而带噪语音信号的谐波结构因为受到噪声信号的干扰后，谱线变得不清晰，甚至无法辨认。经传统基于模型的相位重构方法和文中的改进算法后，虽然语音谱线的清晰度都有所改善，即不同程度的增强了语音信号，但明显的是，与最初纯净语音信号的相位差频谱结构相比较，前者缺失了不少重要信息，而后者的相位谱恢复了带噪语音信号中丢失的纯净相位的谐波结构，语音部分的谱线更为完整清晰，也与纯净语音信号的相位差更为相似，验证了文中改进算法对语音信号的增强效果的有效性。

从图5和图6可以看出，对比经两种相位重构的语音增强算法后的增强语音的波形和频谱，文献[4]算法仅仅是在语音信号的浊音段有效抑制了噪声，且有不少的语音失真；而改进的相位重构算法不仅在语音信号的浊音段，而且在清音段也实现了去噪效果，且减少了语音失真，更接近于纯净语音波形，更好地保持了语音频谱特性。

另外，从表1和表2的结果表明，通过文中提出的方法，增强后语音的感知质量和可懂度在各种信噪比及不同的背景噪声下明显提高。与文献[4]算法对比，SP01语音的信噪比平均提高了1.57 dB，语音质量感知评估指标平均提高了0.09；SP15语音的信噪比平均提高了3.21 dB，语音质量感知评估指标平均提高了0.15。进一步证实了笔者提出的改进算法可以更有效地改善语音的可懂度，降低了语音失真。

4 结束语

笔者深入分析了传统基于模型的相位重构的语音增强算法，针对其清音段相位用带噪语音相位代替导致语音失真和听觉不连贯的问题，提出了用信噪比信息与时频特征重构谐波相位的新方法，能够有效改善语音的连贯性，提高可懂度；同时，提出一种改进的TSNR算法估计先验信噪比，利用其改进二元假设模型的幅值估计并结合重构相位进行语音增强。实验结果表明，相比文献算法，笔者提出的新算法在信噪比和语音质量感知评估指标方面具有更明显的提高，有效地降低了语音失真，解决了语音不连贯的问题，提高了语音可懂度。